Updated about 12 years ago by Mayer Michael
GModelSpectralLogParabola¶
This class allows a spectrum definition with an energy-dependent index. It follows the formula:
: Normalisation at reference energy
: Index at reference energy
: Curvature
: Pivot energy (reference energy)
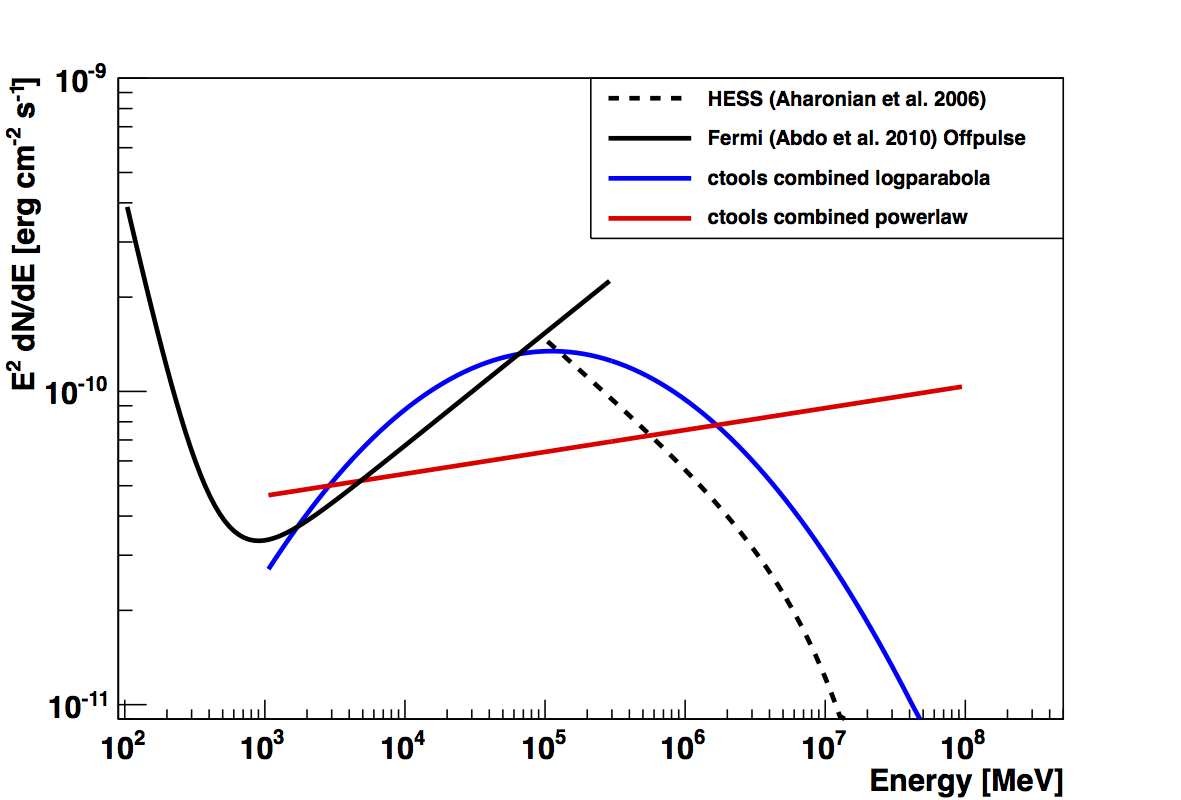
A first test of applying this model to real data from Fermi LAT and HESS is attached.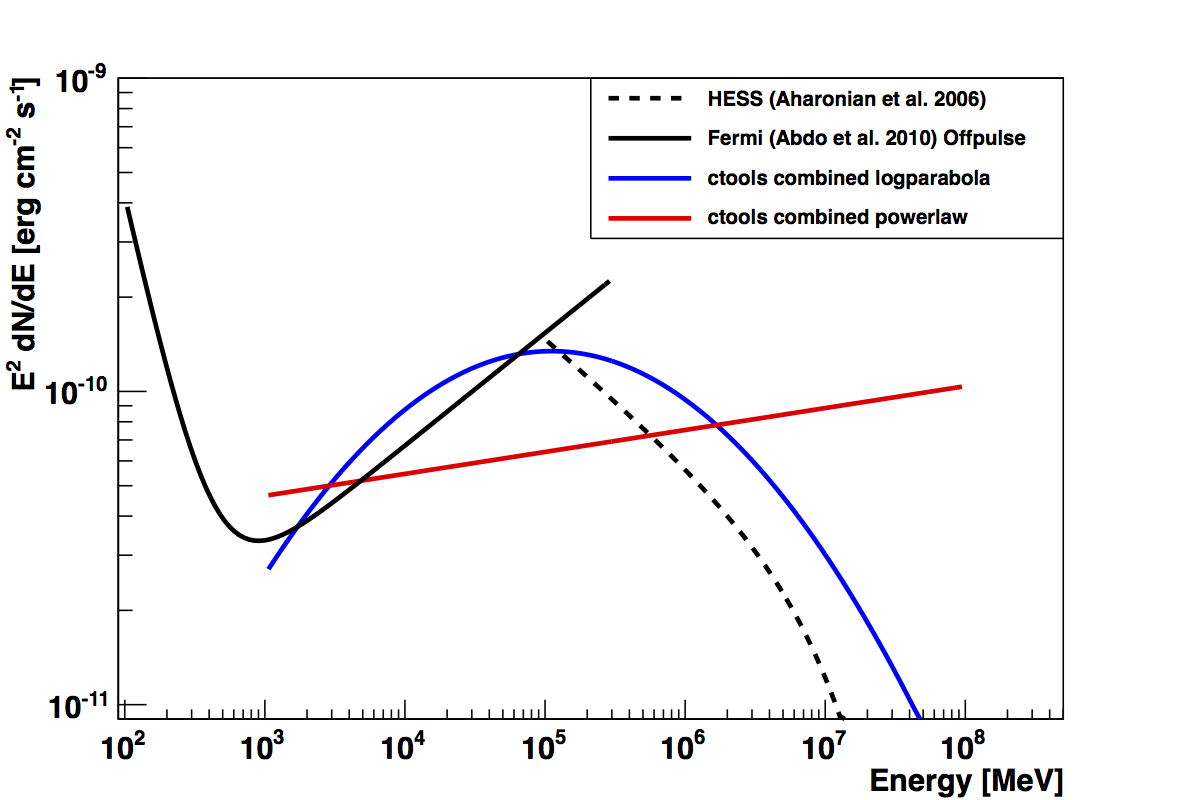
ScienceTools implementation¶
Below the code that is implemented in the Fermi-LAT ScienceTools. Note that the index and curvature are defined as positive values here, as the negative sign is explicitely implemented in the formula.
double LogParabola::value(optimizers::Arg & xarg) const {
::Pars pars(m_parameter);
double energy = dynamic_cast<optimizers::dArg &>(xarg).getValue();
double x = energy/pars[3];
double my_value = pars[0]*std::pow(x, -(pars[1] + pars[2]*std::log(x)));
return my_value;
}
double LogParabola::derivByParam(optimizers::Arg & xarg,
const std::string & paramName) const {
::Pars pars(m_parameter);
double energy = dynamic_cast<optimizers::dArg &>(xarg).getValue();
double x = energy/pars[3];
double logx = std::log(x);
double dfdnorm = std::pow(x, -(pars[1] + pars[2]*logx));
int iparam = -1;
for (unsigned int i = 0; i < pars.size(); i++) {
if (paramName == pars(i).getName()) {
iparam = i;
}
}
if (iparam == -1) {
throw optimizers::ParameterNotFound(paramName, getName(),
"LogParabola::derivByParam");
}
enum ParamTypes {norm, alpha, beta, Eb};
switch (iparam) {
case norm:
return dfdnorm*m_parameter[norm].getScale();
case alpha:
return -pars[0]*logx*dfdnorm*m_parameter[alpha].getScale();
case beta:
return -pars[0]*logx*logx*dfdnorm*m_parameter[beta].getScale();
case Eb:
return value(xarg)/pars[3]*(pars[1] + 2.*pars[2]*logx)
*m_parameter[Eb].getScale();
default:
break;
}
return 0;
}
Monte Carlo Method¶
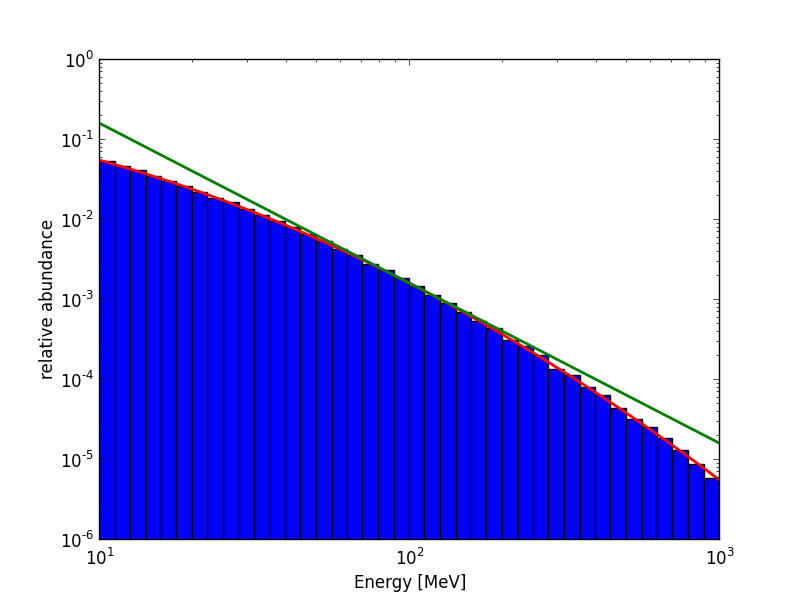
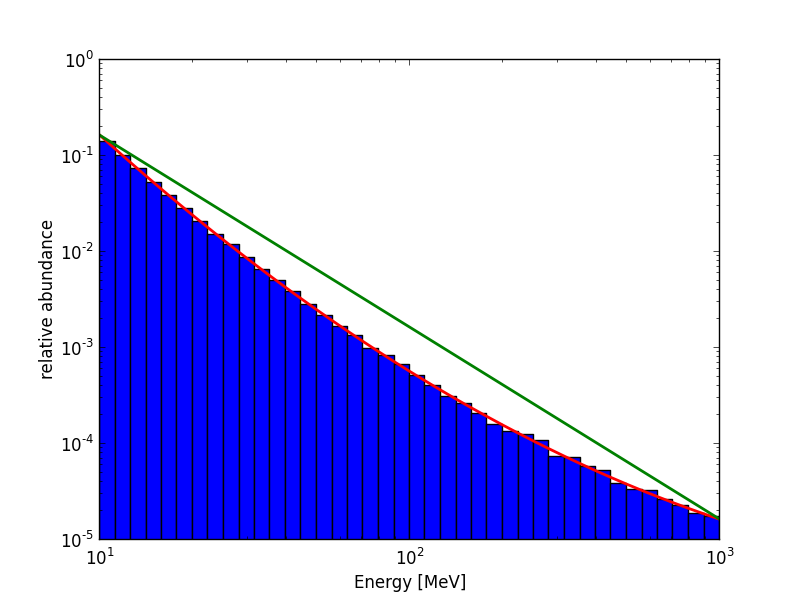
the method GModelSpectralLogParabola::mc(GEnergy emin, GEnergy emax, GRan ran) returns a random energy following the LogParabola distribution. The following plots have been produced using normalised LogParabola with the Parameters index=-2, curvature=+-0.2 and E0=100MeV. 100000 Events have been simulated. Red lines show the underlying LogParabola model while green lines correspond to the respective powerlaws which are used as function for the "rejection sampling method". 

{{fnlist}}