Bug #1142
Pull distribution of CTA RadialAcceptance model shows offset in Normalization
| Status: | Closed | Start date: | 02/09/2014 | |
|---|---|---|---|---|
| Priority: | High | Due date: | ||
| Assigned To: |  Knödlseder Jürgen | % Done: | 100% | |
| Category: | - | |||
| Target version: | 00-09-00 | |||
| Duration: |
Description
Everything is in the title. Plots will be posted later.
background_normalization_problem.png (47.9 KB)
background_sigma_problem.png (46.4 KB)
model_bgd.xml 
(510 Bytes)
background_normalization_solved.png (47.8 KB)
background_sigma_solved.png (46.5 KB)
Recurrence
No recurrence.
History
#1
Updated by Knödlseder Jürgen almost 11 years ago
- Status changed from New to In Progress
- % Done changed from 0 to 80
It appears that the integration precision of 1e-5 in GObservation::npred_spec was not enough for the highly erratic background model file function. Increasing the precision to 1e-6 is not perfect, but results in a pull distribution that is much more close to a Gaussian.
Here as example the Npred dependence on the integration precision. Using a dumb numerical integration, a value of 1017061.8 is expected:
| Precision | Npred | Absolute difference | Relative difference |
| 1e-5 | 1016370.3 | -691.5 | -0.07% |
| 1e-6 | 1017138.6 | 76.8 | +0.008% |
| 1e-7 | 1017059.2 | -2.6 | -0.0003% |
| 1e-8 | 1017062.1 | 0.3 | 0.00003% |
So even with 1e-5 the relative difference is small, but when a long run and the background model is concerned, such a value may be perceptible.
#2
Updated by Knödlseder Jürgen almost 11 years ago
- File background_normalization_problem.png added
- File background_sigma_problem.png added
- File model_bgd.xml added
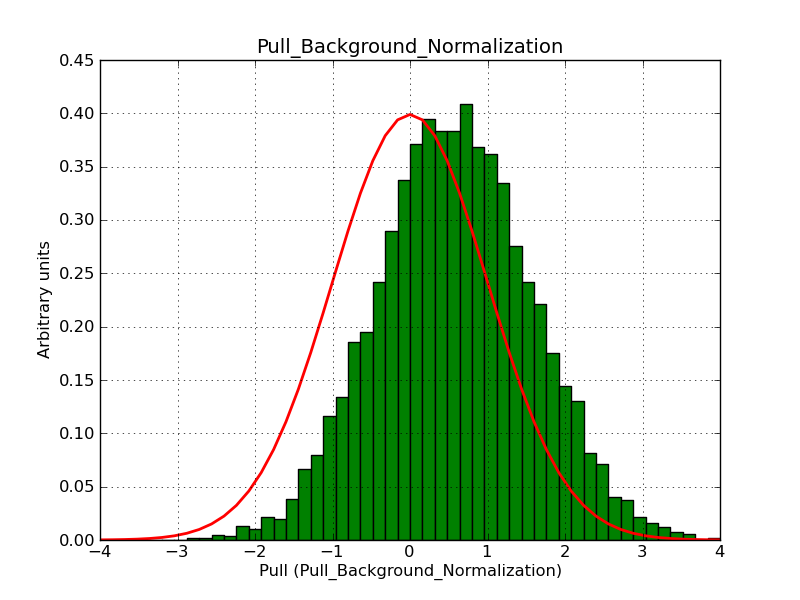
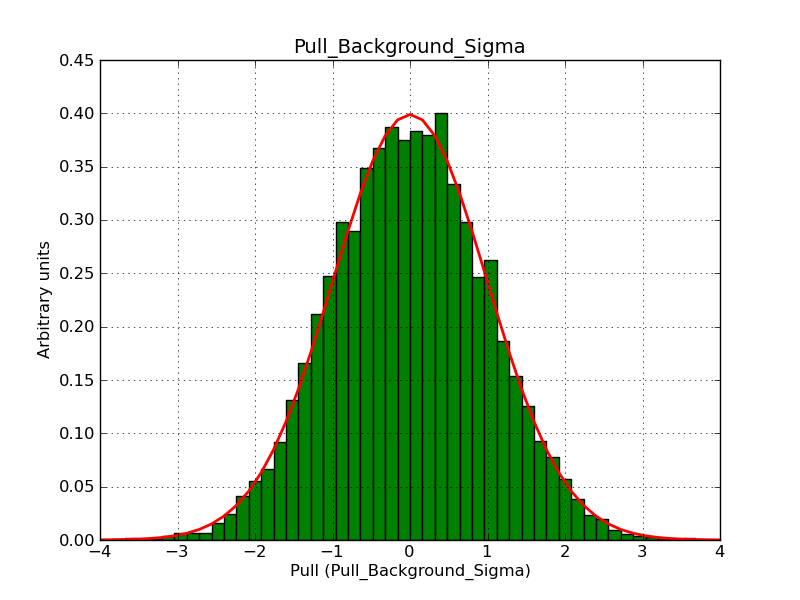
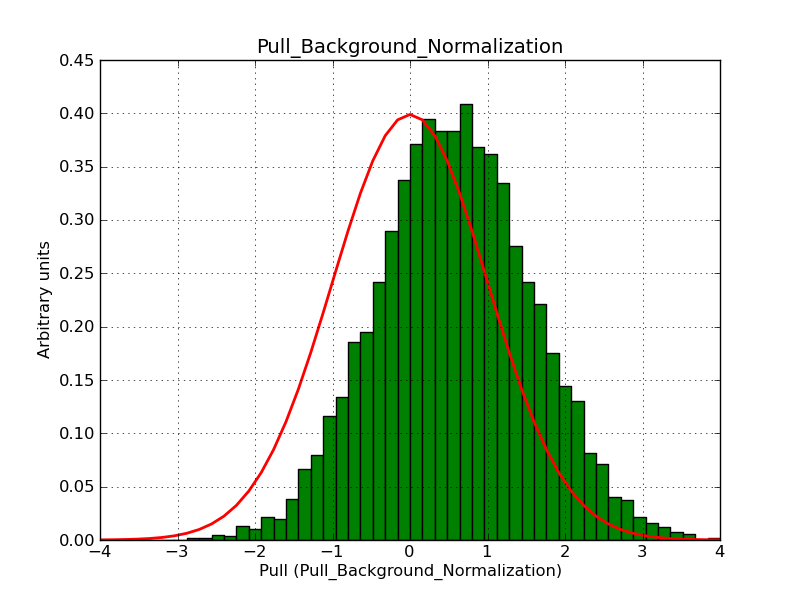
Below the pull distributions for gammalib-00-08-01. The background normalization is obviously systematically shifted towards too high values. The XML file for this simulation can be found here: model_bgd.xml. The deadtime correction factor has been set to 1 to make sure that the problem is not related to the deadtime correction.
 |
 |
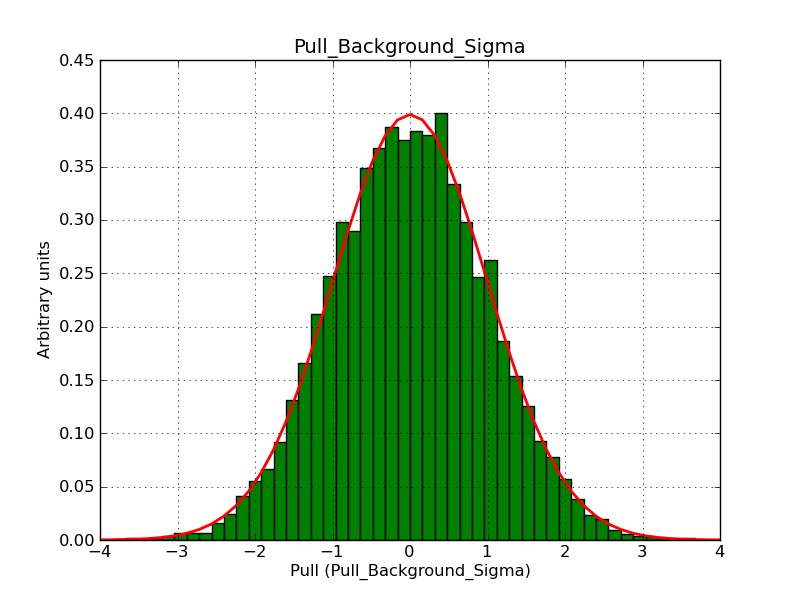#3
Updated by Knödlseder Jürgen almost 11 years ago
- File background_normalization_solved.png added
- File background_sigma_solved.png added
- Status changed from In Progress to Feedback
- % Done changed from 80 to 100
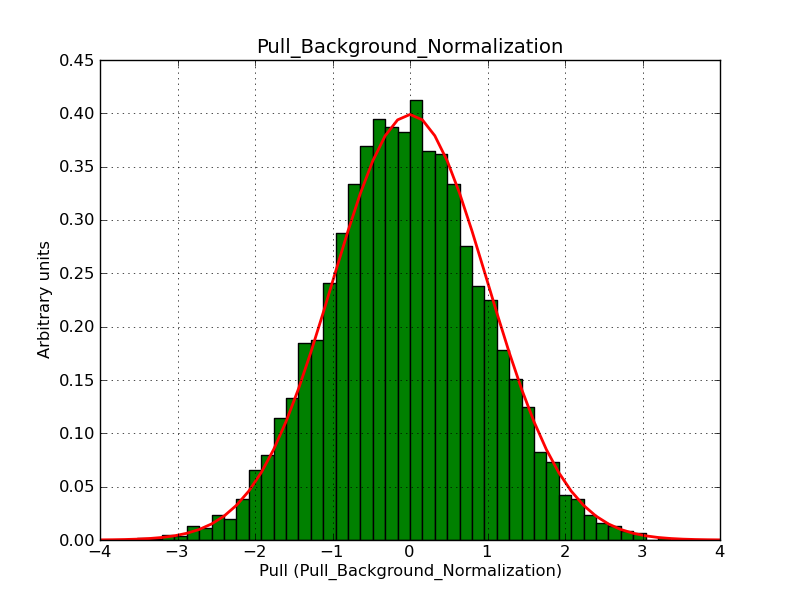
Below the pull distributions for an integration precision of 1e-6. This obviously fixes the problem, at the expense of a moderate increase in computing time.
 |
 |
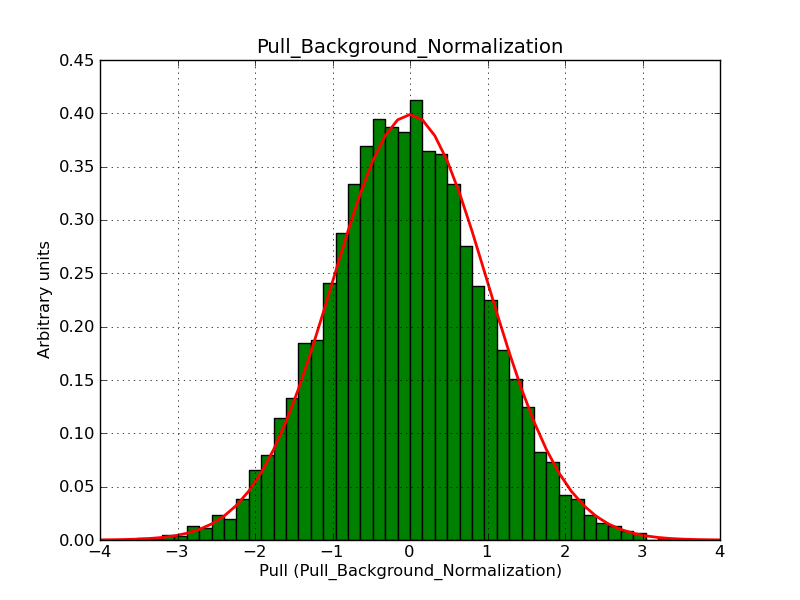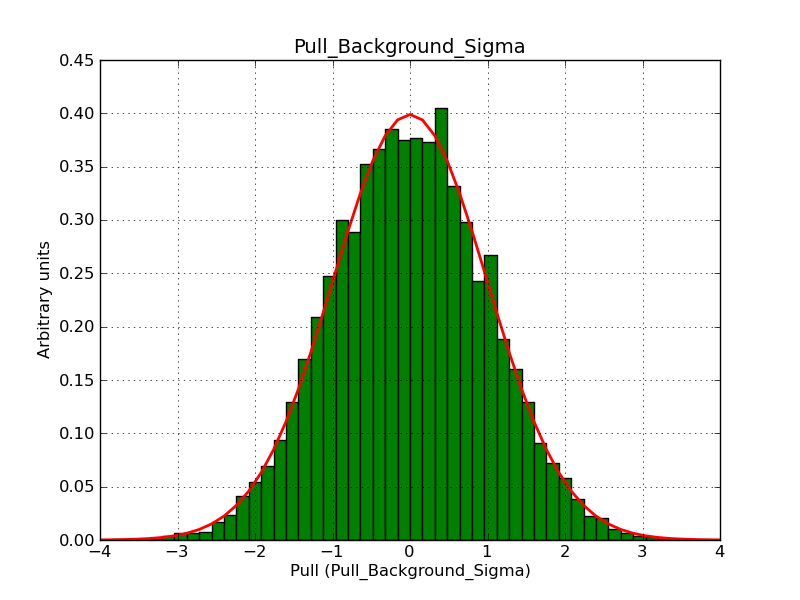#4
Updated by Knödlseder Jürgen over 10 years ago
- Status changed from Feedback to Resolved
- Target version changed from 00-08-02 to 00-09-00
Skip 0.8.2 release.
#5
Updated by Knödlseder Jürgen over 10 years ago
- Status changed from Resolved to Closed