Action #392
Feature #34: Implement MC methods for all spectral models
Implement MC method for GModelSpectralExpPlaw
| Status: | Closed | Start date: | 02/20/2012 | |
|---|---|---|---|---|
| Priority: | Normal | Due date: | ||
| Assigned To: | % Done: | 100% | ||
| Category: | - | Estimated time: | 4.00 hours | |
| Target version: | 00-08-00 | |||
| Duration: |
Recurrence
No recurrence.
History
#1
 Updated by Knödlseder Jürgen over 12 years ago
Updated by Knödlseder Jürgen over 12 years ago
- Target version deleted (
00-06-00)
#2
 Updated by Knödlseder Jürgen over 12 years ago
Updated by Knödlseder Jürgen over 12 years ago
- Target version set to 00-07-00
#3
 Updated by Knödlseder Jürgen about 12 years ago
Updated by Knödlseder Jürgen about 12 years ago
Here some Python code implementing an exponential cutoff power law random number generator. n is the number of random samples to be drawn, alpha the exponent and Lambda the cutoff value.
x = []
y=[]
for i in range(10*n):
y.append(xmin - (1./Lambda)*log(1.-random()))
while True:
ytemp=[]
for i in range(10*n):
if random()<pow(y[i]/float(xmin),-alpha):ytemp.append(y[i])
y = ytemp
x = x+y
q = len(x)-n
if q==0: break;
if (q>0):
r = range(len(x))
shuffle(r)
xtemp = []
for j in range(len(x)):
if j not in r[0:q]:
xtemp.append(x[j])
x=xtemp
break;
if (q<0):
y=[]
for j in range(10*n):
y.append(xmin - (1./Lambda)*log(1.-random()))
#4
 Updated by Knödlseder Jürgen about 12 years ago
Updated by Knödlseder Jürgen about 12 years ago
Here another code:
/*
Simulate power law with cut-off x^(-alpha)*exp(-lambda*x)
To simulate power-law with cutoff , one can generate an
exponentially distributed random number using the formula
above (as k>0 and integer, so k start at 1)
and then accept or reject it with probability p or 1 - p
respectively (i.e accept U1 <p or reject U1>p, and
U1 is a uniform [0,1] random variable),
where p = (x/x_min)^(-alpha) and x_min=1.
http://www.santafe.edu/~aaronc/powerlaws/
*/
double rand_gen::powerlaw_dist(double alpha, double lamda)
{
double x;
do {
x = exponential_dist(lamda);
} while (pow(x,-1*alpha) < uniform_dist(0.,1.));
return (x);
}
/*
To simulate exponential distribution exp(-lambda*x), the inverse
method is used.
The cumulative distribution function for the exponential
distribution is:1-exp(-lambda*x). The inversion function
is -log(1-U)/lambda. The simplified form is -log(U)/lambda,
where U is a uniform [0,1] random variable.
http://cg.scs.carleton.ca/~luc/rnbookindex.html
*/
double rand_gen::exponential_dist(double lambda)
{
return(-1*log(uniform_dist(0.,1.))/lambda);
}
#5
 Updated by Knödlseder Jürgen about 12 years ago
Updated by Knödlseder Jürgen about 12 years ago
- File expplaw-check.png added
The method has now been implemented.
The above algorithm has proven to be very inefficient. We now use first the analytical power law MC to draw an energy, and then use a rejection method to see whether we should accept the sample or reject it. This works in a reasonable amount of time.
The following plot shows the simulation results for 5 hours of Crab observations with CTA (269285 photons simulated).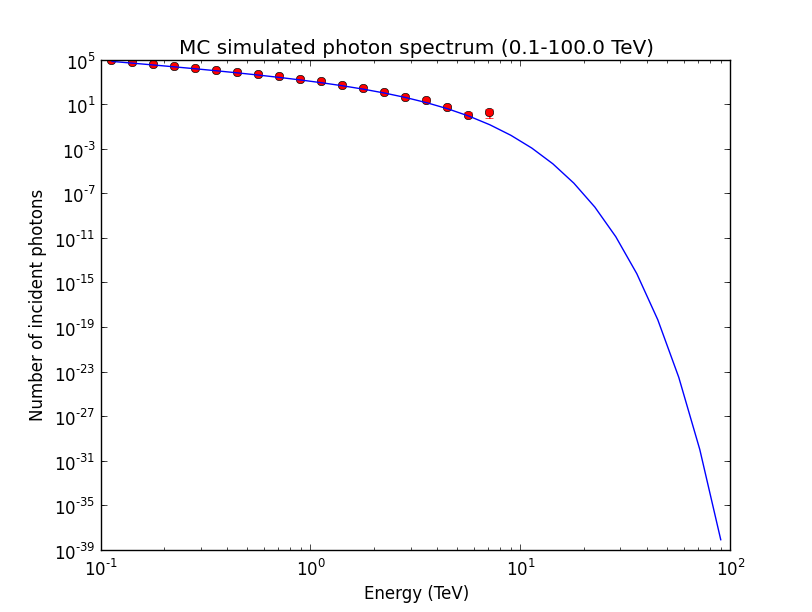
#6
 Updated by Knödlseder Jürgen about 12 years ago
Updated by Knödlseder Jürgen about 12 years ago
- Status changed from New to Feedback
- % Done changed from 0 to 100
- Remaining (hours) changed from 4.0 to 0.0
#7
 Updated by Knödlseder Jürgen about 12 years ago
Updated by Knödlseder Jürgen about 12 years ago
- Target version changed from 00-07-00 to 00-08-00
#8
 Updated by Knödlseder Jürgen about 12 years ago
Updated by Knödlseder Jürgen about 12 years ago
- Target version deleted (
00-08-00)
#9
 Updated by Knödlseder Jürgen about 12 years ago
Updated by Knödlseder Jürgen about 12 years ago
- Target version set to 00-08-00
#10
 Updated by Knödlseder Jürgen about 12 years ago
Updated by Knödlseder Jürgen about 12 years ago
- Status changed from Feedback to Closed