Feature #1017
Improve GWcs.solidangle method
| Status: | Closed | Start date: | 12/04/2013 | |
|---|---|---|---|---|
| Priority: | High | Due date: | ||
| Assigned To: | % Done: | 100% | ||
| Category: | - | |||
| Target version: | 00-08-00 | |||
| Duration: |
Description
The docstring of the `GWcs.omega` method to compute the pixel solid angle mentions “Something more intelligent should be implemented in the future.”
http://gammalib.sourceforge.net/doxygen/classGWcs.html#e2c412e6435e058fb80c04b958f47f79
I started a diffuse emission analysis for large parts of the sky and am using AIT images.
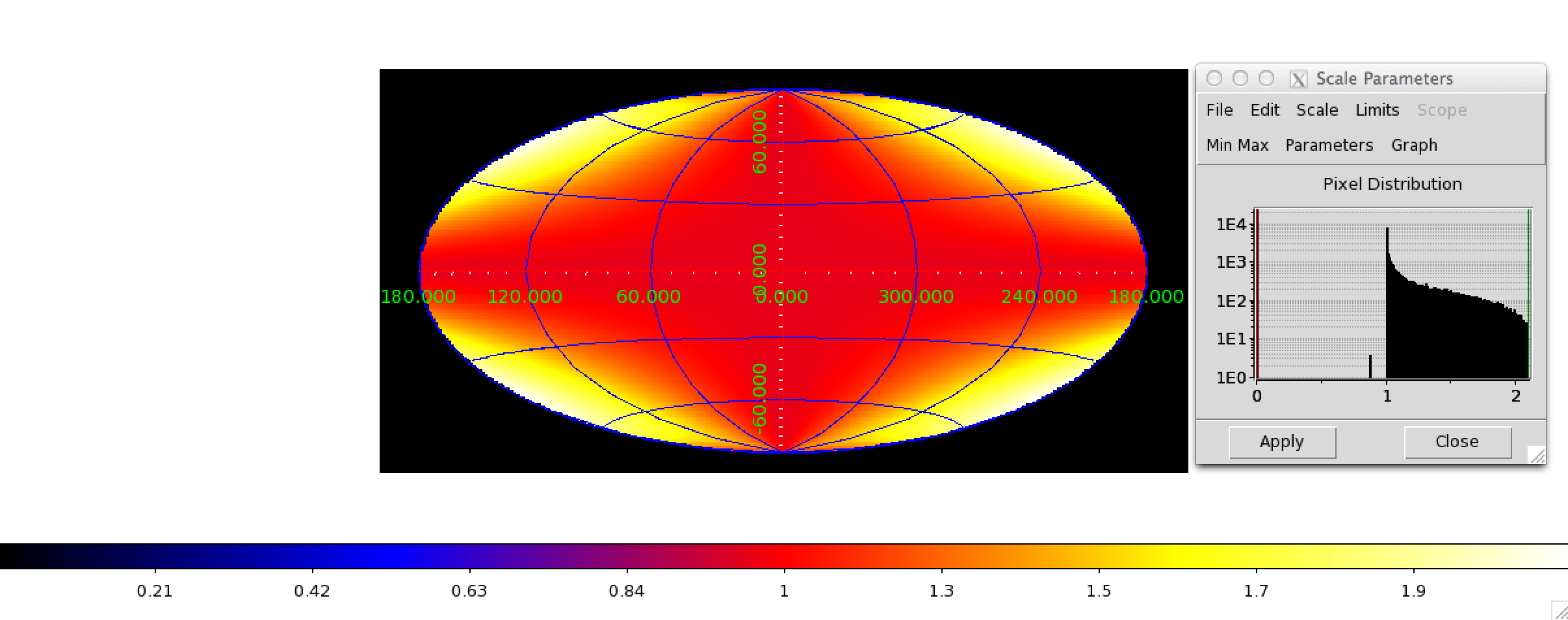
I thought in AIT images the pixel area is almost constant, but I find that using the current method the pixel area varies by a factor 2.
See https://github.com/cdeil/gammalib-tutorials/blob/master/make_omega_image.py and attached screenshot.
Is this an error in the omega calculation for the current method or are AIT pixels not really equal-area?
I’ve looked around a bit, and I’d be happy to implement a more precise method, but I’m not sure which is best.
http://en.wikipedia.org/wiki/Spherical_trigonometry#Area_and_spherical_excess
http://www.mathworks.de/de/help/map/ref/areaint.html
http://stackoverflow.com/questions/4681737/how-to-calculate-the-area-of-a-polygon-on-the-earths-surface-using-python
Recurrence
No recurrence.
History
#1
 Updated by Knödlseder Jürgen about 11 years ago
Updated by Knödlseder Jürgen about 11 years ago
Deil Christoph wrote:
The docstring of the `GWcs.omega` method to compute the pixel solid angle mentions “Something more intelligent should be implemented in the future.”
http://gammalib.sourceforge.net/doxygen/classGWcs.html#e2c412e6435e058fb80c04b958f47f79
Right. I was looking for some general formulae for solid angles of pixels for various WCS projections, yet I did not find anything. So the dumb method just takes the corners of a pixel to estimate the solid angle, which probably isn’t very good if the pixels are considerably distorted.
If you have an explicit formula for some of the projections one can add this to the projection class by overloading the
virtual double omega(const GSkyPixel& pixel) const;method of the
GWcs base class.#2
 Updated by Deil Christoph about 11 years ago
Updated by Deil Christoph about 11 years ago
I’ve asked if someone knows a good method on the astropy mailing list:
http://mail.scipy.org/pipermail/astropy/2013-December/002937.html
#3
 Updated by Knödlseder Jürgen about 11 years ago
Updated by Knödlseder Jürgen about 11 years ago
- Priority changed from Normal to High
Back in 2009, I asked the question already to Mark Calabretta (Mister WCS). He was not aware of some software doing this job:
managed to get a general conversion. Do you know about a collection
of formula that can be used to derive the solid angles of individual
image pixels or are there some subroutines in the wcslib to do this
task (or are there some subroutines available for idl)?
Dear Jürgen,
It’s difficult in general to evaluate pixel areas analytically - a
square pixel in the plane of projection may become severely distorted
when projected back onto the sphere. Cylindrical projections and equal
area projections are really the only easy cases, numerical methods must
be used for the others. However, I’m not aware of any software that
can do this.Regards,
Mark Calabretta
I put the priority of this issue to High as we should really not forget about this. Maybe we need a maths geek who works out the formula, or who can propose a solid numerical method.
#4
 Updated by Deil Christoph about 11 years ago
Updated by Deil Christoph about 11 years ago
It seems the usual algorithm is to project the pixel corners on the sphere and then using Girard’s theorem:
http://mail.scipy.org/pipermail/astropy/2013-December/002941.html
http://montage.ipac.caltech.edu/docs/algorithms.html
There is a stand-alone C version of the core Montage algorithm:
http://mail.scipy.org/pipermail/astropy/2013-December/002940.html
https://github.com/astrofrog/python-reprojection/pull/3
I think Montage has a non-free license, but maybe this part will become available as open source:
http://montage.ipac.caltech.edu/docs/download.html
https://github.com/astrofrog/python-reprojection/issues/1
If not we can always re-implement it (or the sub-set of solid angle computation we need), but presumably there’s some corner cases to get right and the existing implementation is well-tested.
#5
 Updated by Deil Christoph about 11 years ago
Updated by Deil Christoph about 11 years ago
- Assigned To set to Deil Christoph
https://github.com/astrofrog/python-reprojection/blob/master/reproject/overlapArea.c
is now under a BSD license, i.e. I think we can include a copy in gammalib.
Tom and I are currently improving it and once it’s in good shape (no global variables, good test coverage) in a week or two we can put a copy in gammalib:
https://github.com/astrofrog/python-reprojection/issues
The core functionality implemented there is flux-conserving reprojection, not only computation of pixel solid angles.
I think we want flux-conserving reprojection methods in gammalib as well, e.g. it could come in handy to stack runs into survey maps or to reproject background models in the FOV system onto sky maps.
Jürgen, do you agree?
If yes, can you please propose a place and outline what API you think would be nice (class method? function?)
#6
 Updated by Knödlseder Jürgen about 11 years ago
Updated by Knödlseder Jürgen about 11 years ago
Note that GWcs.omega() has been renamed to GWcs.solidangle()
#7
 Updated by Deil Christoph about 11 years ago
Updated by Deil Christoph about 11 years ago
- Subject changed from Improve GWcs.omega method? to Improve GWcs.solidangle method
- Assigned To changed from Deil Christoph to Owen Ellis
- Target version set to 2nd coding sprint
Ellis, could you please implement the method to compute the solid angle of a given pixel described here?
http://mail.scipy.org/pipermail/astropy/2013-December/002940.html
#8
 Updated by Owen Ellis about 11 years ago
Updated by Owen Ellis about 11 years ago
- Status changed from New to In Progress
#9
 Updated by Owen Ellis about 11 years ago
Updated by Owen Ellis about 11 years ago
- File image_issue.png added
I replaced the existing solid angle script the following:
{
GSkyDir dir1 = pix2dir(GSkyPixel(pixel.x()-0.5, pixel.y()-0.5));
GSkyDir dir2 = pix2dir(GSkyPixel(pixel.x()+0.5, pixel.y()-0.5));
GSkyDir dir3 = pix2dir(GSkyPixel(pixel.x()+0.5, pixel.y()+0.5));
GSkyDir dir4 = pix2dir(GSkyPixel(pixel.x()-0.5, pixel.y()+0.5));
GVector vec1 = dir1.celvector();
GVector vec2 = dir2.celvector();
GVector vec3 = dir3.celvector();
GVector vec4 = dir4.celvector();
double angle1 = std::acos(cross(vec2, (cross(vec1, vec2))) * cross(vec2, (cross(vec3, vec2))));
double angle2 = std::acos(cross(vec3, (cross(vec2, vec3))) * cross(vec3, (cross(vec4, vec3))));
double angle3 = std::acos(cross(vec4, (cross(vec3, vec4))) * cross(vec4, (cross(vec1, vec4))));
double angle4 = std::acos(cross(vec1, (cross(vec4, vec1))) * cross(vec1, (cross(vec2, vec1))));
double solidangle = (angle1 + angle2 + angle3 + angle4) - (2 * gammalib::pi);
return solidangle;
}
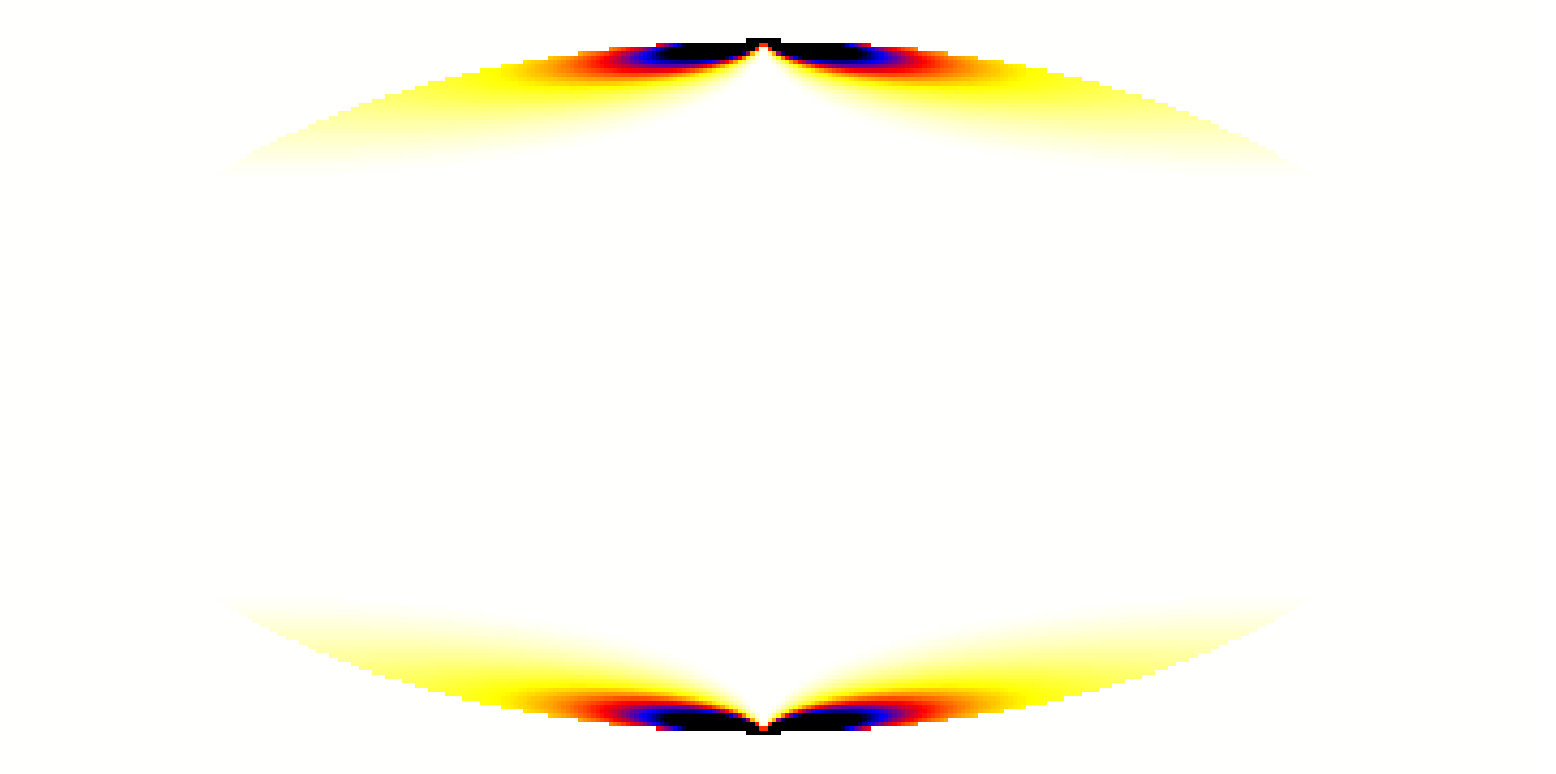
Which gives clearly incorrect results: I would expect the map to have pixel values of approx 1 but they are around 1e-4 (and quite variable) - see attached ds9 screenshot - the test script is here: https://gist.github.com/ellisowen/8473696
I shall start de-bugging, but wondered if you could see anything obviously wrong with the method/script?
Also, would it be best to include this as an alternative to the original solidangle calculation, or as a replacement?
(Branch is here: https://github.com/ellisowen/gammalib/compare/issue_1017)
#10
 Updated by Knödlseder Jürgen about 11 years ago
Updated by Knödlseder Jürgen about 11 years ago
1e-4 looks like an issue with square degrees versus steradians. Note that the solid angle is computed in steradians, hence it’s probably not so bad. 1 square degree is about 3.05e-4 steradians. All your angles above are in radians.
I guess that for an Aitoff projection, things become really complex when it comes to the pole. Maybe the formula you use can not manage this?
A minor thing, not related to the problems you have. I see
double solidangle = (angle1 + angle2 + angle3 + angle4) - (2 * gammalib::pi);
in your code. Please always use
double solidangle = (angle1 + angle2 + angle3 + angle4) - (2.0 * gammalib::pi);
hence floating points when you mean floating points. I had some issue with such things in the past, I think on FreeBSD (don’t remember exactly).
#11
 Updated by Knödlseder Jürgen about 11 years ago
Updated by Knödlseder Jürgen about 11 years ago
- File aitoff-solid-angle.png added
I got the following result with this code:
//
double a;
double b;
double c;
// Angle 1
a = dir1.dist(dir3);
b = dir4.dist(dir3);
c = dir4.dist(dir1);
double angle1 = std::acos((std::cos(a) - std::cos(b)*std::cos(c))/(std::sin(b)*std::sin(c)));
// Angle 2
a = dir4.dist(dir2);
b = dir2.dist(dir3);
c = dir3.dist(dir4);
double angle2 = std::acos((std::cos(a) - std::cos(b)*std::cos(c))/(std::sin(b)*std::sin(c)));
// Angle 3
a = dir1.dist(dir3);
b = dir1.dist(dir2);
c = dir2.dist(dir3);
double angle3 = std::acos((std::cos(a) - std::cos(b)*std::cos(c))/(std::sin(b)*std::sin(c)));
// Angle 4
a = dir4.dist(dir2);
b = dir4.dist(dir1);
c = dir1.dist(dir2);
double angle4 = std::acos((std::cos(a) - std::cos(b)*std::cos(c))/(std::sin(b)*std::sin(c)));
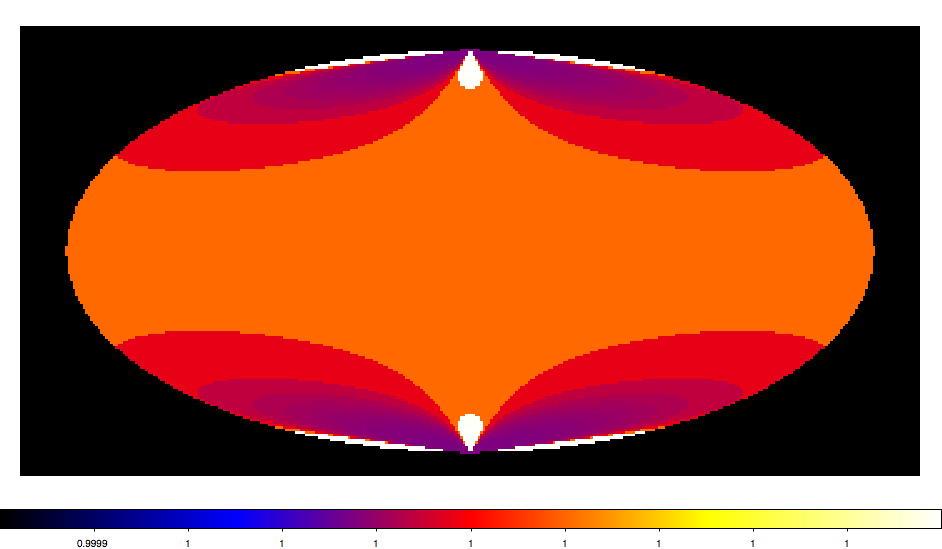
Looks reasonable. The code uses spherical triangles to compute the inner angles of the Polygon. I guess you code attempts to do the same thing, but maybe some stuff got mixed up.
My code is not yet optimized as I repeat distance computations. But I just wanted to see whether this works.
#12
 Updated by Knödlseder Jürgen about 11 years ago
Updated by Knödlseder Jürgen about 11 years ago
Here some optimized code that gives the same result.
// Compute angular distances between pixel corners
double a12 = dir1.dist(dir2);
double a13 = dir1.dist(dir3);
double a14 = dir1.dist(dir4);
double a23 = dir2.dist(dir3);
double a24 = dir2.dist(dir4);
double a34 = dir3.dist(dir4);
// Angle 1
double a = a13;
double b = a34;
double c = a14;
double angle1 = std::acos((std::cos(a) - std::cos(b)*std::cos(c))/(std::sin(b)*std::sin(c)));
// Angle 2
a = a24;
b = a23;
c = a34;
double angle2 = std::acos((std::cos(a) - std::cos(b)*std::cos(c))/(std::sin(b)*std::sin(c)));
// Angle 3
a = a13;
b = a12;
c = a23;
double angle3 = std::acos((std::cos(a) - std::cos(b)*std::cos(c))/(std::sin(b)*std::sin(c)));
// Angle 4
a = a24;
b = a14;
c = a12;
double angle4 = std::acos((std::cos(a) - std::cos(b)*std::cos(c))/(std::sin(b)*std::sin(c)));
I pushed this into
issue_1017_jk. We should test all projections before we decide to merge this in to make sure that the computations are okay.#13
 Updated by Knödlseder Jürgen about 11 years ago
Updated by Knödlseder Jürgen about 11 years ago
- % Done changed from 0 to 50
Just think: can still be optimized a little more as there are repeated cos and sin calls.
#14
 Updated by Owen Ellis about 11 years ago
Updated by Owen Ellis about 11 years ago
- % Done changed from 50 to 0
Okay, I think I also have figured out the problem with my method. I avoid calling cos and sin so much, so maybe it would need less optimizing?
I’ll push it to https://github.com/ellisowen/gammalib/compare/issue_1017 when I’ve done a couple of checks!
#15
 Updated by Owen Ellis about 11 years ago
Updated by Owen Ellis about 11 years ago
- % Done changed from 0 to 50
(Changed % done by accident so just returned it to 50%)
#16
 Updated by Owen Ellis about 11 years ago
Updated by Owen Ellis about 11 years ago
- File new_aitoff.png added
- Status changed from In Progress to Pull request
Pushed to https://github.com/ellisowen/gammalib/compare/issue_1017 - please review.
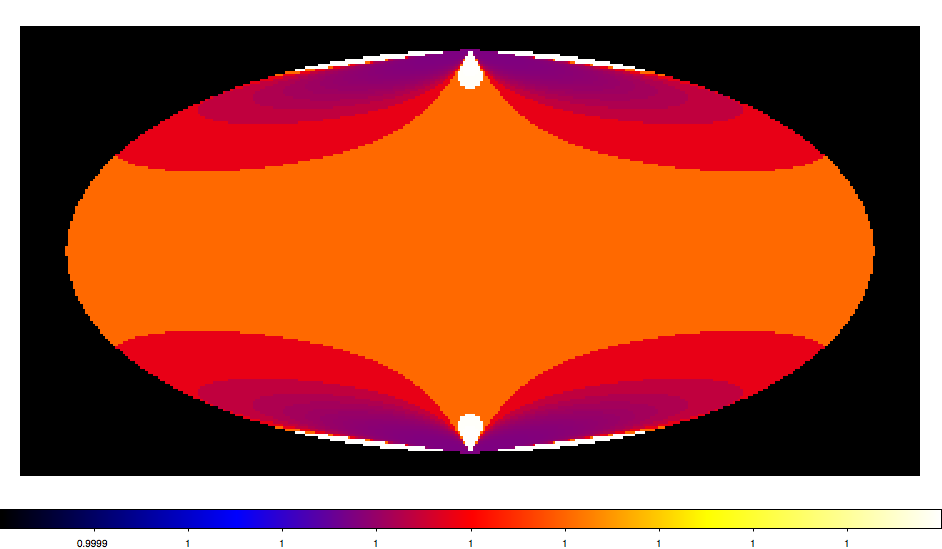
Attached check projection ds9 screenshot (it’s not very clear, but values seem reasonable).
#17
 Updated by Knödlseder Jürgen about 11 years ago
Updated by Knödlseder Jürgen about 11 years ago
- Status changed from Pull request to In Progress
Sorry to say that there is still some problem.
I tried your code with a pixel size of (0.5 x 0.5) instead of (1.0 x 1.0), and when you integrate over the map you get a total solid angle that is 4 times too large. With the trigonometric formula the correct values are obtained.
For the (1.0 x 1.0) pixel size I still get an error of a few percent when being close to the pole, so the formula seem only to be approximate.
Can you point to where you took the cross-product / dot-product formula from? Could it be that they only work for cartesian coordinates?
#18
 Updated by Knödlseder Jürgen about 11 years ago
Updated by Knödlseder Jürgen about 11 years ago
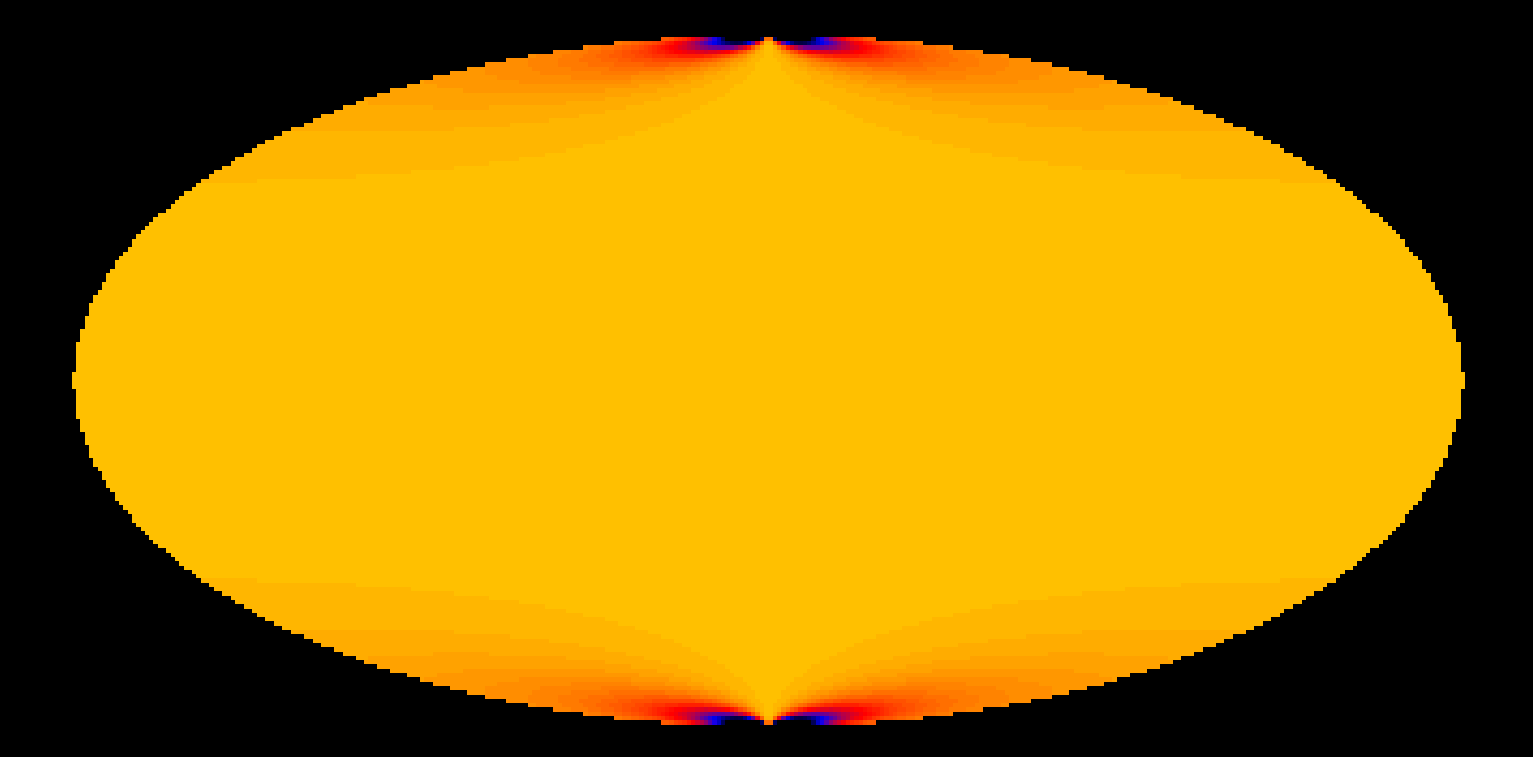
Addition: I checked for the CAR projection, and here the formula obviously does not work at all (there is basically no variation over the sky, while for a CAR projection the pixels become smaller when going to the poles).
#19
 Updated by Knödlseder Jürgen about 11 years ago
Updated by Knödlseder Jürgen about 11 years ago
- File make_solidangle_image.py
 added
added - File solidangle_AIT.png added
- File solidangle_AZP.png added
- File solidangle_CAR.png added
- File solidangle_MER.png added
- File solidangle_STG.png added
- File solidangle_TAN.png added
- Status changed from In Progress to Feedback
- % Done changed from 50 to 100
I modified the code so that both methods can be toggled using a compiler flag. This allows you to investigate this further. Pushed into issue_1017_jk.
I optimized the code a little more for the trigonometric version, and also take care of the possibility that a pixel touches the pole, reducing the polygon to a triangle. I tested the code with the script attached.
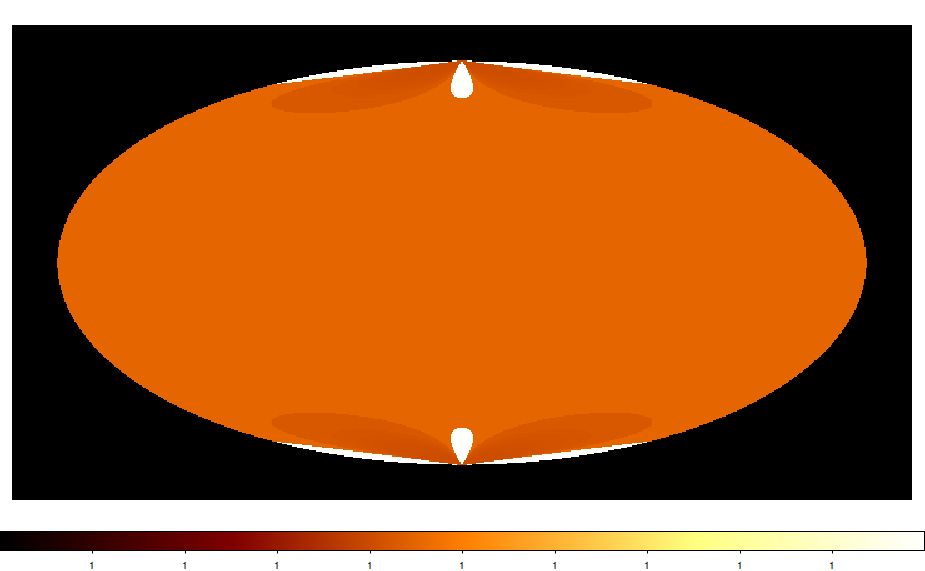
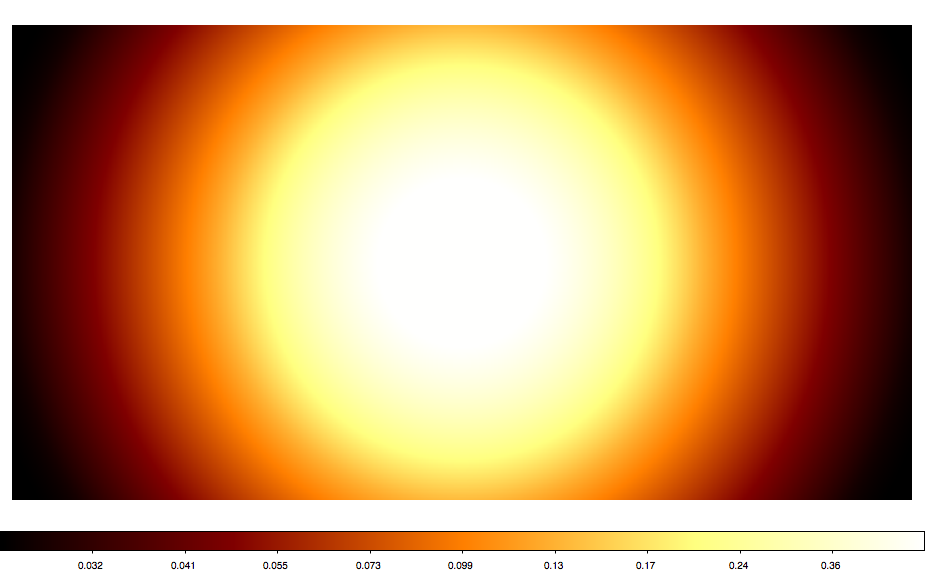
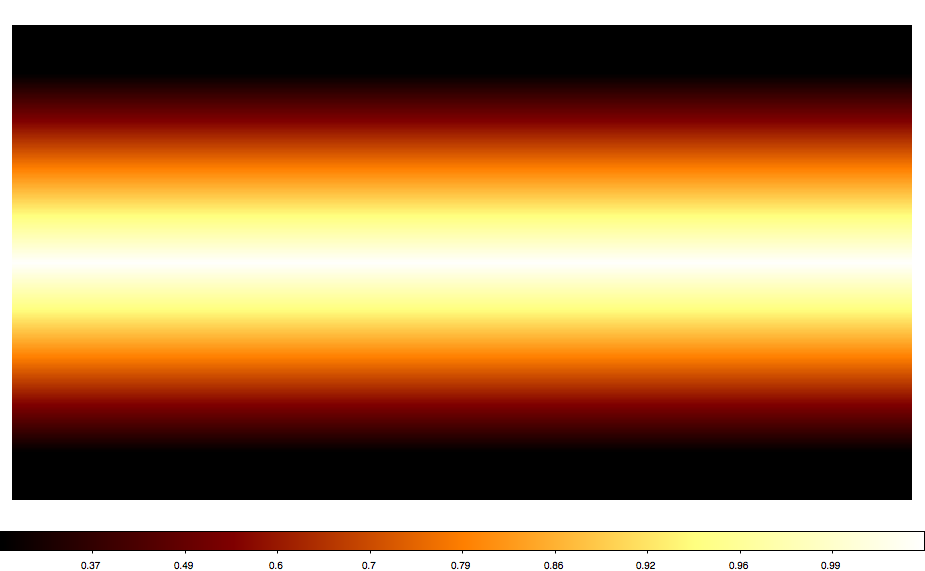
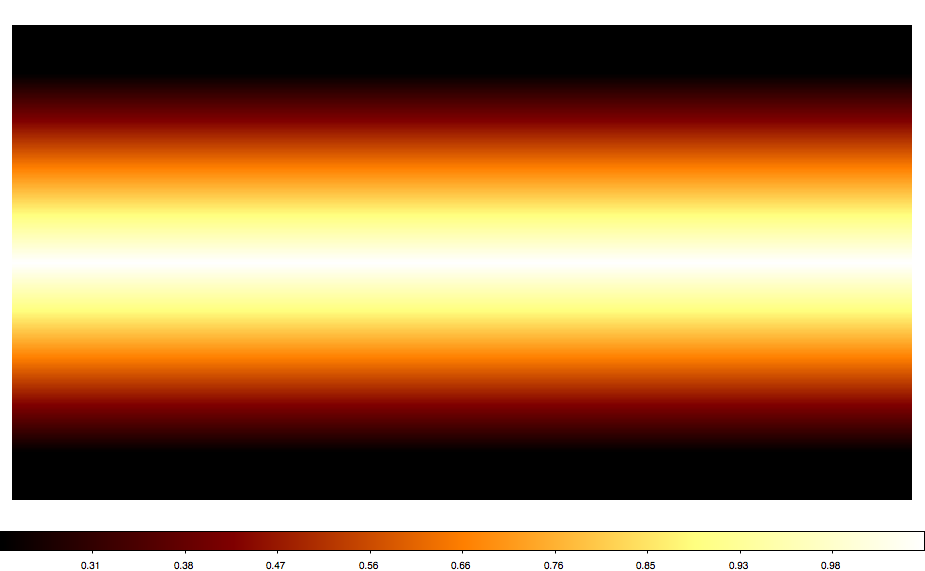
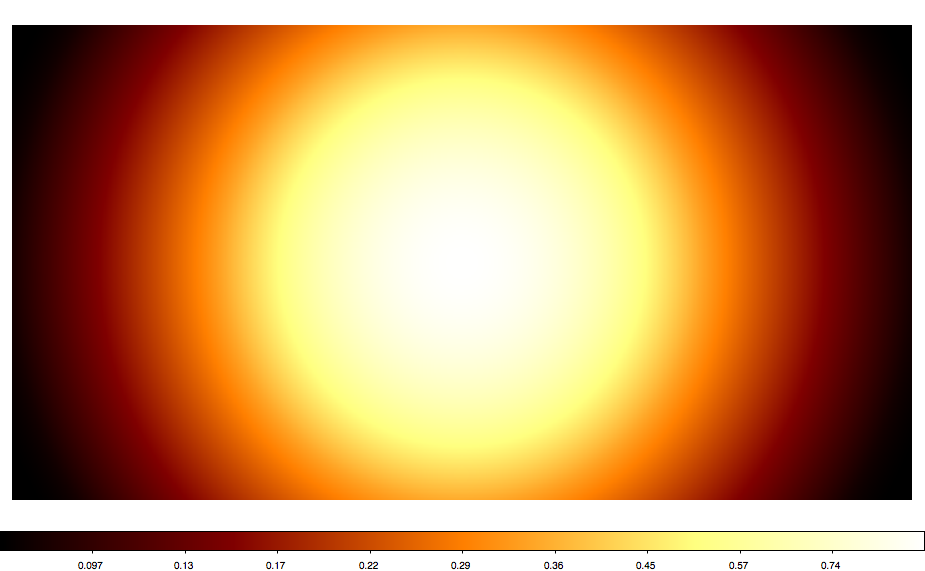
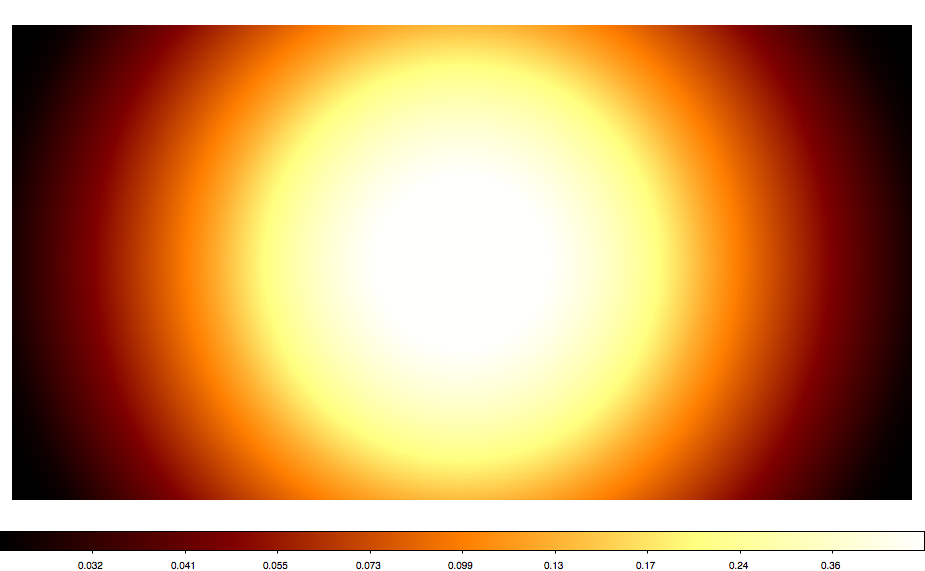
Below also a number of all sky maps produced by the script for various projections. They seem to be all okay (at least visually). The script now also computes the total solid angle of the map, and at least non of the projections led to a NaN. AIT and CAR give 4 pi as expected. Eventually, some more testing would be nice.
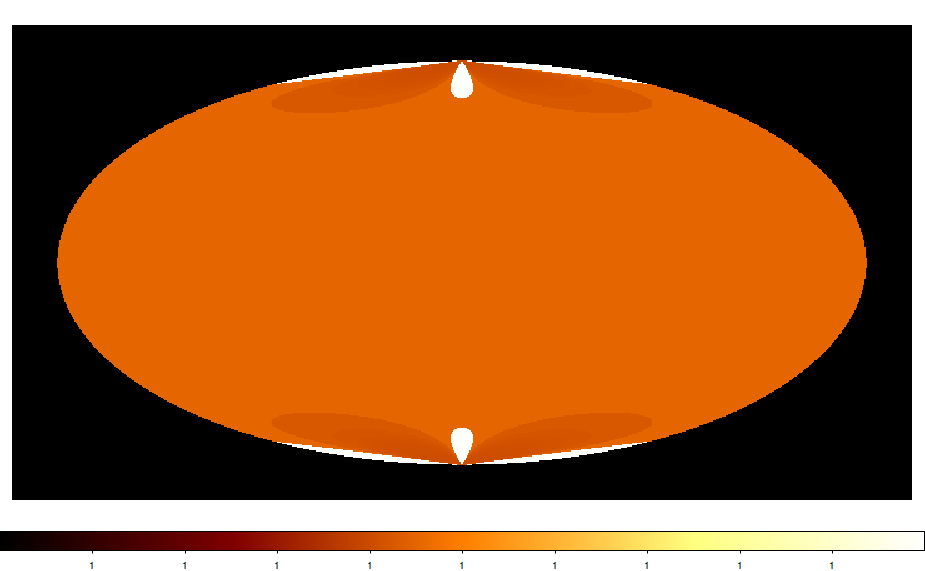 |
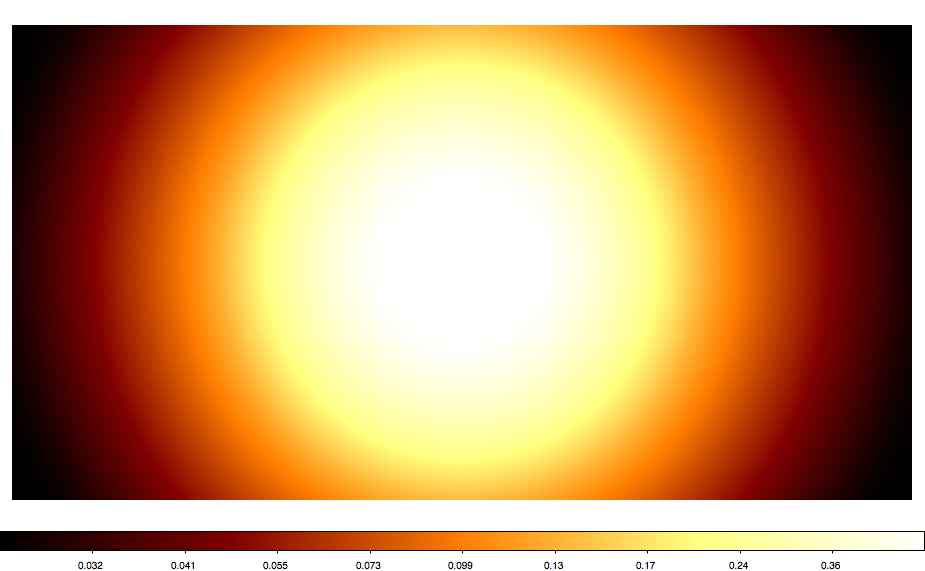 |
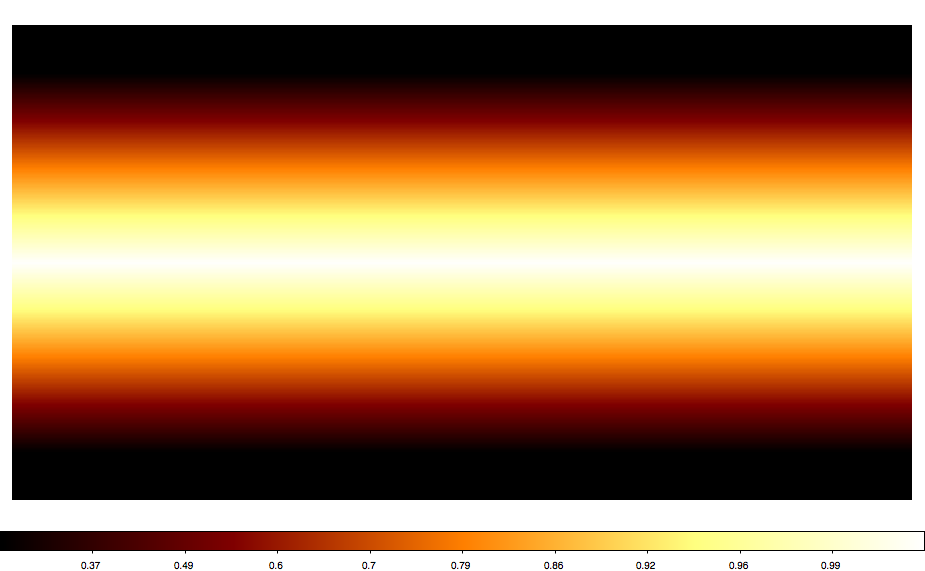 |
 |
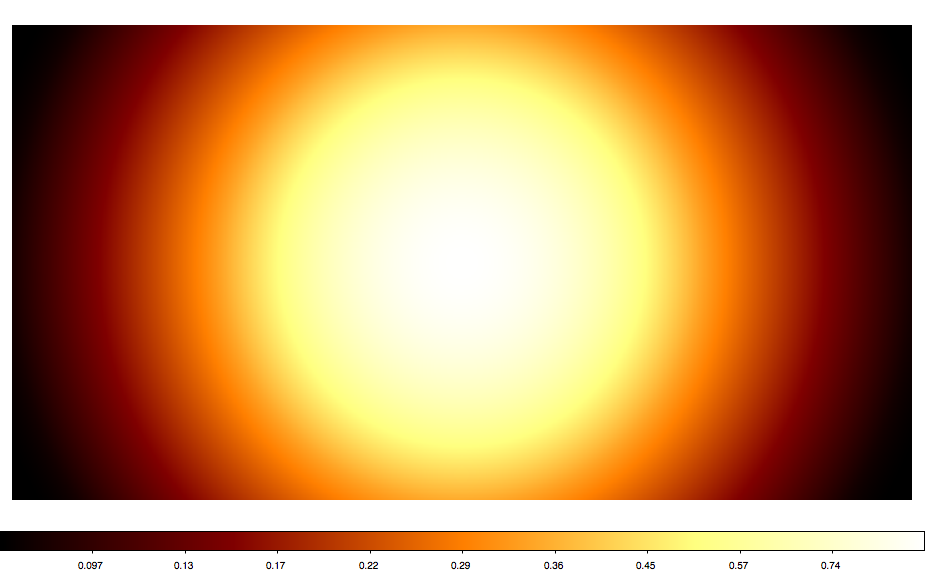 |
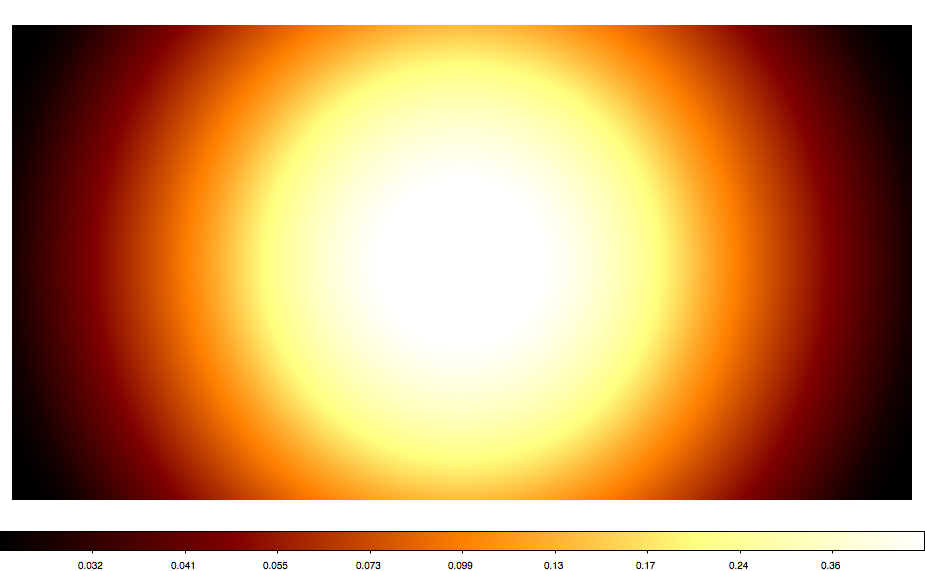 |
#20
 Updated by Deil Christoph about 11 years ago
Updated by Deil Christoph about 11 years ago
Knödlseder Jürgen wrote:
Can you point to where you took the cross-product / dot-product formula from? Could it be that they only work for cartesian coordinates?
I asked on the astropy mailing list how to best compute this and this is a formula from Michael Droettboom gave:
http://mail.scipy.org/pipermail/astropy/2013-December/002940.html
I didn’t think about it or look at your or Ellis’s code in detail.
If your implementation with trigonometric functions looks OK we should simply use that, I guess.
One more thing that could be worth testing is very small pixels (say 0.1, 0.01, 0.001 deg size) to make sure that rounding errors with doubles will be acceptable for CTA.
#21
 Updated by Owen Ellis about 11 years ago
Updated by Owen Ellis about 11 years ago
The factor of 4 issue you mentioned I think is because I just noticed I hadn’t adapted the term ((gammalib::pi * (1.0/180.0)) in the solid angle formula to account for different pixel sizes.
However, I’d tend to agree with Christoph - the formula in my code clearly isn’t quite right (even with the above problem corrected), and it’s not yet clear to me how to fix the other issues. So I think it would perhaps better to just use your working code?
#22
 Updated by Knödlseder Jürgen about 11 years ago
Updated by Knödlseder Jürgen about 11 years ago
Deil Christoph wrote:
Knödlseder Jürgen wrote:
Can you point to where you took the cross-product / dot-product formula from? Could it be that they only work for cartesian coordinates?
I asked on the astropy mailing list how to best compute this and this is a formula from Michael Droettboom gave:
http://mail.scipy.org/pipermail/astropy/2013-December/002940.htmlI didn’t think about it or look at your or Ellis’s code in detail.
If your implementation with trigonometric functions looks OK we should simply use that, I guess.
One more thing that could be worth testing is very small pixels (say 0.1, 0.01, 0.001 deg size) to make sure that rounding errors with doubles will be acceptable for CTA.
I check with very small pixels (0.0001 deg) and it’s okay. I see numerical noise at the 1e-4 level.
But you’re right, my initial trigonometric code has numerical problems. I finally managed to solve them by dividing internally the pixel into two triangles and using Huilier’s theorem (see http://mathworld.wolfram.com/SphericalExcess.html). This also needs a little less trigonometric functions, though it requires tangens instead of sine or cosine, which is a bit slower (see Computation Benchmarks).
#23
 Updated by Knödlseder Jürgen about 11 years ago
Updated by Knödlseder Jürgen about 11 years ago
- Target version changed from 2nd coding sprint to 00-08-00
Owen Ellis wrote:
The factor of 4 issue you mentioned I think is because I just noticed I hadn’t adapted the term ((gammalib::pi * (1.0/180.0)) in the solid angle formula to account for different pixel sizes.
However, I’d tend to agree with Christoph - the formula in my code clearly isn’t quite right (even with the above problem corrected), and it’s not yet clear to me how to fix the other issues. So I think it would perhaps better to just use your working code?
For the moment I left all options in the code, can be selected through #define. In the long run we may remove the obsolete code, but we better keep for the moment the possibility to play with the options.
I now merged all the stuff in devel.
#24
 Updated by Knödlseder Jürgen about 11 years ago
Updated by Knödlseder Jürgen about 11 years ago
- Status changed from Feedback to Closed