Feature #1412
Implement GModelSpatialEllipticalGauss
| Status: | Closed | Start date: | 01/26/2015 | |
|---|---|---|---|---|
| Priority: | Normal | Due date: | ||
| Assigned To: | % Done: | 100% | ||
| Category: | - | |||
| Target version: | 1.0.0 | |||
| Duration: |
Description
To be able to reproduce results of current IACTs, we need to implement an elliptical Gaussian model.
Recurrence
No recurrence.
Related issues
History
#1
 Updated by Deil Christoph about 10 years ago
Updated by Deil Christoph about 10 years ago
Is it necessary to duplicate the radial and elliptical models in Gammalib?
http://gammalib.sourceforge.net/doxygen/classGModelSpatial.html
E.g. Sherpa only has a Gaussian model, it has elongation parameters, the default is that they are frozen, i.e. the user gets a radial Gaussian model:
http://cxc.harvard.edu/sherpa/ahelp/sigmagauss2d.html
This page also shows the formulas to implement the elongation in a generic way that could be re-used by all elongated models.
But maybe a single efficient implementation is no longer possible because some analytical integrals are needed for unbinned analysis?
#2
 Updated by Knödlseder Jürgen about 10 years ago
Updated by Knödlseder Jürgen about 10 years ago
There could be eventually some re-organising in the future of these models, but for the time being we have separated radial from elliptical models. Doing now a Gaussian in addition to a disk model is a no brainer, it should even work much better than the disk as it has no sharp edges.
I also see one difference between radial and elliptical models: for radial models I’m sure they are done correctly on the sphere (hence they could be used for example for a Fermi-LAT analysis to describe Loop I). For elliptical models I’m not really sure in what system the computation is done, I think it’s cartesian.
#3
 Updated by Mayer Michael almost 10 years ago
Updated by Mayer Michael almost 10 years ago
- File pulldist.png added
- Status changed from New to Feedback
- Assigned To set to Mayer Michael
- Target version set to 1.0.0
- % Done changed from 0 to 90
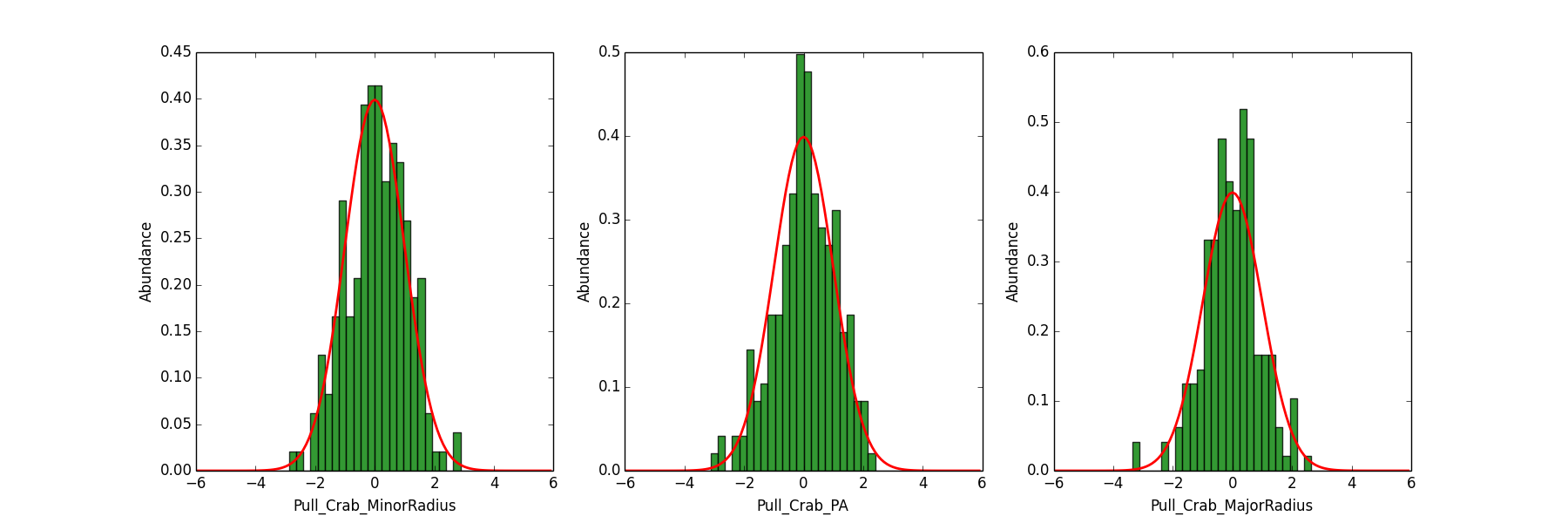
I have implemented the new class GModelSpatiallEllipticalGauss, which was actually just copying the majority of the code from the elliptical disk model. I still have to update some parts of the documentation I guess (which is quite hard since the formula is quite lengthy).
Nevertheless, the code seems to work properly. However, I encountered rather long computation times when I run cspull. By constraining the parameter boundaries closer to the real values some speed could be gained but an fit of a “standard” CTA observation still takes about 20 secs on my MacBook.
Therefore, I reduced the observation time in cspull to 900sec (instead of 1800). I quickly ran 200 trials and created some pull distribution for the parameters (which are attached).
I encountered one issue, we might want to think about:
In the base class GModelSpatialElliptical, the parameter names of the axes are set to “MinorRadius” and “MajorRadius”. For the Gaussian, I’d rather go for “MinorAxis” and “MajorAxis” since “radius” is not the proper name when it comes to a Gaussian. Should we therefore reorganise the elliptical classes to move the two size parameters to the derived classes, or should GModelSpatialEllipticalGauss::init_members() just rename the parameters?
I furthermore created a test case, which passes all tests (analogous to the disk model).
Everything is available on branch 1412-implement-GModelSpatialEllipticalGauss
#4
 Updated by Deil Christoph almost 10 years ago
Updated by Deil Christoph almost 10 years ago
Thanks, Michael!
Sherpa parametrises the elongated models like 2D Gaussian with width and ellipticity (see http://cxc.harvard.edu/sherpa/ahelp/gauss2d.html).
Astropy uses semi-major and semi-minor axis like you did here.
Does one of you know which one is more stable for morphology fitting?
I remember when I tried to make a HESS source catalog of elongated Gaussians with Sherpa getting the fits to converge in complex regions was a big problem even with good starting values for the optimizer and I eventually gave up.
Do you have a test that shows that the position angle is fit robustly near the theta = 0 deg = 360 deg ?
In any case, I’m +1 to put in what you have now in devel and maybe encourage people to try out elongated models in the mailing list, so that potential issues are noticed before the 1.0 release.
#5
 Updated by Knödlseder Jürgen almost 10 years ago
Updated by Knödlseder Jürgen almost 10 years ago
We may indeed change the parameters, one could see what is more stable.
There is in fact a fundamental problem with major and minor axis, which is that you cannot guarantee that at the end the major axis is in fact the longer of both axes (a fit may drive it to a smaller value than the minor axis).
With ellipticity one can constrain the parameter in a way that the major axis is always the longer axis.
#6
 Updated by Deil Christoph almost 10 years ago
Updated by Deil Christoph almost 10 years ago
For reference, here’s the parametrisation Astropy uses:
http://astropy.readthedocs.org/en/latest/api/astropy.modeling.functional_models.Gaussian2D.html
The also have the option to initialise the parameters from a matrix, but that’s not the parametrisation used in the fit.
If I had to guess and decide on a parametrisation without a study (which is not trivial to do to cover all typical CTA use cases for fitting elongated models to see if it’s stable), I’d pick the Sherpa (width, elongation) parametrisation.
#7
 Updated by Mayer Michael almost 10 years ago
Updated by Mayer Michael almost 10 years ago
Thanks for the links Christoph. I used exactly the same formula as astropy.
Changing the parameters to width and ellipticity should probably already happen in the GModelSpatialElliptical base class, right? Then we would have to change the elliptical disk model accordingly.
If we agree that we want to go that way, I can try to apply these changes. What do you think?
Jürgen, should that happen in the branch for this issue, or is this something which deserves another issue/change request?
#8
 Updated by Deil Christoph almost 10 years ago
Updated by Deil Christoph almost 10 years ago
Since probably none of us will have time for a detailed study, I’ve asked for advice here:
http://mail.scipy.org/pipermail/astropy/2015-February/003608.html
I’m +1 to merge whatever you have now in devel since it’s not clear if we should change to another parametrisation ... increases the chances of me and other trying it out on a simulated CTA GPS or the real HESS GPS data.
#9
 Updated by Deil Christoph almost 10 years ago
Updated by Deil Christoph almost 10 years ago
I’ve discussed this with Axel a bit.
Probably both the Astropy and Sherpa parametrisation is unstable for roughly circular sources,
because the position angle jumps when one of the two width parameters gets larger than the other.
This might have been the problem when I tried to make a HESS survey catalog of elongated Gaussians,
and in any case for CTA Galactic analysis we want a tool gives robustly converging elongated model fits for all sources, even the ones that are roughly circular.
One parametrisation that might be stable is CXX, CXY and CYY from SExtractor, see the section 10.6.1 in the manual:
https://www.astromatic.net/pubsvn/software/sextractor/trunk/doc/sextractor.pdf
It might be worthwile to use this internally or to implement this as an alternative parametrisation.
This is similar to spectral models where in some parametrisations problems occur, e.g. in the HESS software we have 2 power-law parametrisations and 3 exponential-cutoff power-law parametrisations implemented.
#10
 Updated by Knödlseder Jürgen almost 10 years ago
Updated by Knödlseder Jürgen almost 10 years ago
Thanks for discussing this. The actual implementation is in fact stable as there is no jump in position angle, but what is called major axis can in fact become smaller than the minor axis.
#11
 Updated by Mayer Michael almost 10 years ago
Updated by Mayer Michael almost 10 years ago
Why not change the names from “major” and “minor” to “axis1” and “axis2”? Accordingly, there would be no problem if one is larger than the other.
#12
 Updated by Deil Christoph almost 10 years ago
Updated by Deil Christoph almost 10 years ago
+1 to call the axes “A”, “B” or “1”, “2” instead of “major” and “minor” and then explain via documentation that the user has to look afterwards themselves which one is the major and minor one.
PS: the latest version of the branch can be seen here:
https://github.com/gammalib/gammalib/compare/1412-implement-GModelSpatialEllipticalGauss
#13
 Updated by Knödlseder Jürgen almost 10 years ago
Updated by Knödlseder Jürgen almost 10 years ago
Before making any decision I would like to analyse the real stability of the actual code (for example to see how an ellipse is fitted where the PA starting value differs by 45 degrees, etc.)
Alternatively, I’d like to try replacing minor_axis by eccentricity, i.e. minor_axis^2 = major_axis^2 (1 - eccentricity^2). This allows to constrain the eccentricity to the interval [0,1], making sure that the major_axis is always the major axis. I’d like to compare the stability of that approach to the actual implementation.
#14
 Updated by Knödlseder Jürgen almost 10 years ago
Updated by Knödlseder Jürgen almost 10 years ago
- Status changed from Feedback to Closed
- % Done changed from 90 to 100
I merged the code into the devel branch. I created the new issue #1448 to follow up the discussion about fit stability. Close this one now.