Action #1060
Investigate whether a more precise curvature matrix computation is needed
| Status: | Closed | Start date: | 01/07/2014 | |
|---|---|---|---|---|
| Priority: | High | Due date: | ||
| Assigned To: | % Done: | 100% | ||
| Category: | - | Estimated time: | 0.00 hour | |
| Target version: | 1.0.0 | |||
| Duration: |
Description
See #1009 for a discussion on possible problems arising from the actual curvature matrix computation.
The second order derivatives are actually dropped from the curvature matrix computation. So far this was fine, but it could lead to problems in case of strongly correlated errors. It is not yet clear whether this is really the problem, but it should be checked whether a more precise curvature matrix computation impacts the result (as test case, a precise analytical computation of the curvature matrix could be implemented for a specific model).
Recurrence
No recurrence.
Related issues
History
#1
 Updated by Knödlseder Jürgen almost 11 years ago
Updated by Knödlseder Jürgen almost 11 years ago
It seems at least that this problem does not occur in the Fermi/LAT Science Tools (see issue #1004), hence it should be possible to solve this problem also for GammaLib.
The Fermi/LAT Science Tools use the minuit2 package, from which the ROOT::Minuit2::MnHesse function is called. Here the relevant code in optimizers/src/NewMinuit.cxx:
// Call Minuit's MIGRAD to find the minimum of the function
int NewMinuit::find_min(int verbose, double tol, int TolType) {
find_min_only(verbose, tol, TolType); //!< Here the minimum is searched for
std::vector<double> parValues;
m_stat->getFreeParamValues(parValues);
hesse(verbose); //!< Here the error computation is done
m_stat->setFreeParamValues(parValues);
return getRetCode();
}
// Call Minuit's MIGRAD to find the minimum of the function
int NewMinuit::find_min_only(int verbose, double tol, int TolType) {
setTolerance(tol, TolType);
std::vector<Parameter> params;
m_stat->getFreeParams(params);
ROOT::Minuit2::MnUserParameters upar;
size_t ii(0);
for (pptr p = params.begin(); p != params.end(); p++, ii++) {
std::ostringstream mangledName;
mangledName << ii << "_" << p->getName();
upar.Add(mangledName.str().c_str(), p->getValue(), 1.0,
p->getBounds().first, p->getBounds().second);
// Q: Is 1.0 the best choice for that parameter?
}
ROOT::Minuit2::MnUserParameterState userState(upar);
ROOT::Minuit2::MnMinimize migrad(m_FCN, userState, m_strategy);
ROOT::Minuit2::FunctionMinimum min = migrad(m_maxEval, m_tolerance);
delete m_min;
m_min = new ROOT::Minuit2::FunctionMinimum(min);
if (verbose > 0) std::cout << *m_min;
if (!min.IsValid()) {
throw Exception("Minuit abnormal termination. No convergence?");
}
m_distance = min.Edm();
std::vector<double> ParamValues;
unsigned int i = 0;
for (pptr p = params.begin(); p != params.end(); p++, i++) {
ParamValues.push_back(m_min->UserParameters().Value(i));
}
m_stat->setFreeParamValues(ParamValues);
setRetCode(checkResults());
return getRetCode();
}
// Call Minuit's HESSE to get a robust estimate of the covariance matrix
void NewMinuit::hesse(int verbose) {
if (!m_min)
throw Exception("Minuit: find_min must be executed before hesse");
ROOT::Minuit2::MnHesse hesse(m_strategy);
#ifndef BUILD_WITHOUT_ROOT
#if ROOT_SVN_REVISION > 23900
hesse(m_FCN, *m_min, m_maxEval);
#else
m_min->UserState() = hesse(m_FCN, m_min->UserParameters(), m_maxEval);
#endif
#else
hesse(m_FCN, *m_min, m_maxEval);
#endif
if (verbose > 0) std::cout << m_min->UserState();
if (!m_min->HasValidCovariance())
throw Exception("Minuit HESSE results invalid");
}
Looking into minuit2, the following code is called in MnHesse.cxx which computes 2x Inverse Hessian == 2x Inverse 2nd derivative matrix:
void MnHesse::operator()(const FCNBase& fcn, FunctionMinimum& min, unsigned int maxcalls) const {
// interface from FunctionMinimum to be used after minimization
// use last state from the minimization without the need to re-create a new state
MnUserFcn mfcn(fcn, min.UserState().Trafo());
MinimumState st = (*this)( mfcn, min.State(), min.UserState().Trafo(), maxcalls);
min.Add(st);
}
MinimumState MnHesse::operator()(const MnFcn& mfcn, const MinimumState& st, const MnUserTransformation& trafo, unsigned int maxcalls) const {
// internal interface from MinimumState and MnUserTransformation
// Function who does the real Hessian calculations
The latter operator contains the Hessian matrix computation.
#2
 Updated by Knödlseder Jürgen almost 11 years ago
Updated by Knödlseder Jürgen almost 11 years ago
- Priority changed from Normal to High
#3
 Updated by Knödlseder Jürgen almost 11 years ago
Updated by Knödlseder Jürgen almost 11 years ago
Here some useful minuit2 links:
- http://seal.web.cern.ch/seal/MathLibs/Minuit2/html/
- http://wwwasdoc.web.cern.ch/wwwasdoc/minuit/node32.html
The error matrix produced by HESSE is used to calculate what Minuit prints as the parameter errors, which therefore contain the effects due to parameter correlations. - http://seal.web.cern.ch/seal/documents/minuit/mnusersguide.pdf
- http://seal.web.cern.ch/seal/documents/minuit/mntutorial.pdf
- http://seal.web.cern.ch/seal/documents/minuit/mnerror.pdf
And here links about the computation of the Hessian matrix:
#4
 Updated by Knödlseder Jürgen almost 11 years ago
Updated by Knödlseder Jürgen almost 11 years ago
Here the non-parallized code in minuit2 for the Hessian computation (does not include the inversion). Looks at the end not so dramatic, just have to find out what’s exactly behind the various quantities. Note that the MnHesse::operator() code should be implemented, but the MnHesse::Hessian code helps to understand better the formulae:
MinimumError MnHesse::Hessian(const MnFcn& mfcn, const MinimumState& st, const MnUserTransformation& trafo) const {
const MnMachinePrecision& prec = trafo.Precision();
// make sure starting at the right place
double amin = mfcn(st.Vec()); //!< Get value at minimum
/*
Error definition of the function. MINUIT defines Parameter errors as the
change in Parameter Value required to change the function Value by up. Normally,
for chisquared fits it is 1, and for negative log likelihood, its Value is 0.5.
If the user wants instead the 2-sigma errors for chisquared fits, it becomes 4,
as Chi2(x+n*sigma) = Chi2(x) + n*n.
*/
// eps returns the smallest possible number so that 1.+eps > 1.
// eps2 returns 2*sqrt(eps)
double aimsag = sqrt(prec.Eps2())*(fabs(amin)+mfcn.Up());
// diagonal Elements first
unsigned int n = st.Parameters().Vec().size();
MnAlgebraicSymMatrix vhmat(n);
MnAlgebraicVector g2 = st.Gradient().G2(); //!< second derivatives
MnAlgebraicVector gst = st.Gradient().Gstep(); //!< step size, how defined?
MnAlgebraicVector grd = st.Gradient().Grad(); //!< first derivatives
MnAlgebraicVector dirin = st.Gradient().Gstep();
MnAlgebraicVector yy(n);
MnAlgebraicVector x = st.Parameters().Vec();
// Loop over all parameters
for(unsigned int i = 0; i < n; i++) {
// Setup initial and minimum step size. Initial step size comes from Gstep
double xtf = x(i);
double dmin = 8.*prec.Eps2()*fabs(xtf);
double d = fabs(gst(i));
if(d < dmin) d = dmin;
// Ncycles() = fStrategy.HessianNCycles() (low=3, medium=5, high=7)
for(int icyc = 0; icyc < Ncycles(); icyc++) {
double sag = 0.;
double fs1 = 0.;
double fs2 = 0.;
// Do 5 cycles. Computes fs1, fs2, sag, d, with d as small as possible that sag is not zero
for(int multpy = 0; multpy < 5; multpy++) {
x(i) = xtf + d;
fs1 = mfcn(x);
x(i) = xtf - d;
fs2 = mfcn(x);
x(i) = xtf;
sag = 0.5*(fs1+fs2-2.*amin); //!< Computes 0.5*step*step*(second derivative)
if(sag > prec.Eps2()) break;
if(trafo.Parameter(i).HasLimits()) {
if(d > 0.5) {
std::cout<<"second derivative zero for Parameter "<<i<<std::endl;
std::cout<<"return diagonal matrix "<<std::endl;
for(unsigned int j = 0; j < n; j++) {
vhmat(j,j) = (g2(j) < prec.Eps2() ? 1. : 1./g2(j));
return MinimumError(vhmat, 1., false);
}
}
d *= 10.;
if(d > 0.5) d = 0.51;
continue;
}
d *= 10.;
}
// Signal if sag is too small
if(sag < prec.Eps2()) {
std::cout<<"MnHesse: internal loop exhausted, return diagonal matrix."<<std::endl;
for(unsigned int i = 0; i < n; i++)
vhmat(i,i) = (g2(i) < prec.Eps2() ? 1. : 1./g2(i));
return MinimumError(vhmat, 1., false);
}
// Keep old second derivative (to check improvement later)
double g2bfor = g2(i);
// Compute parameter derivatives and store step size and function value
g2(i) = 2.*sag/(d*d); //!< Computes numerical second derivative
grd(i) = (fs1-fs2)/(2.*d); //!< Computes numerical first derivative
gst(i) = d; //!< Store step size
dirin(i) = d; //!< Store step size
yy(i) = fs1; //!< Store function value
// Compute a new step size based on the aimed sag
double dlast = d;
d = sqrt(2.*aimsag/fabs(g2(i)));
if(trafo.Parameter(i).HasLimits()) d = std::min(0.5, d); //!< d < 0.5 in case of limits
if(d < dmin) d = dmin; //!< d > dmin
// see if converged
/*
low:
HessianStepTolerance(0.5);
HessianG2Tolerance(0.1);
medium:
HessianStepTolerance(0.3);
HessianG2Tolerance(0.05);
high:
HessianStepTolerance(0.1);
HessianG2Tolerance(0.02);
*/
if(fabs((d-dlast)/d) < Tolerstp()) break;
if(fabs((g2(i)-g2bfor)/g2(i)) < TolerG2()) break;
d = std::min(d, 10.*dlast); //!< Do not increase by more than a factor of 10
d = std::max(d, 0.1*dlast); //!< Do not decrease by more than a factor of 10
}
vhmat(i,i) = g2(i); //!< Store diagonal element
}
// Compute off-diagonal Elements
for(unsigned int i = 0; i < n; i++) {
x(i) += dirin(i);
for(unsigned int j = i+1; j < n; j++) {
x(j) += dirin(j);
double fs1 = mfcn(x); //!< Function evaluation with modified parameters
double elem = (fs1 + amin - yy(i) - yy(j))/(dirin(i)*dirin(j));
vhmat(i,j) = elem; //!< Store the element
x(j) -= dirin(j);
}
x(i) -= dirin(i);
}
return MinimumError(vhmat, 0.);
}
Note that numerical first and second derivatives are computed using first and second order central finite difference approximations:
grd(i) = 0.5*(fs1 - fs2)/step;
g2(i) = (fs1 + fs2 - 2.*fcnmin)/step/step;
step to the smallest possible value.
Note that for the off-diagonal elements uses not central but forward differences. Using central differences would require one more operation (see http://en.wikipedia.org/wiki/Finite_difference).
#5
 Updated by Knödlseder Jürgen about 10 years ago
Updated by Knödlseder Jürgen about 10 years ago
- Assigned To set to Knödlseder Jürgen
- Target version set to 1.0.0
I would like to do this for version 1.0 as we otherwise will have problems with correlated parameters.
#6
 Updated by Knödlseder Jürgen almost 10 years ago
Updated by Knödlseder Jürgen almost 10 years ago
- add new method
errors_hessian()toGObservations - implement
errors_hessian()that will call- a method inspired of the
MnHesse::Hessianclass that computes the Hessian matrix - a method that will compute the errors by inverting the Hessian matrix and returns the square root of the diagonal elements
- a method inspired of the
For the model evaluation for a given parameter value, see GObservation::model_grad. Being in GObservations, the evaluation of the model should by the following pseudo-code:
double f(const GModelPar& par, double dh) {
GModelPar current = par;
par.value(par.value() + dh);
eval();
double f = logL();
par = current;
return f;
}
A test case can be realized using the following:
$ ctobssim RA of pointing (degrees) (0-360) [83.63] Dec of pointing (degrees) (-90-90) [22.01] Radius of FOV (degrees) (0-180) [5.0] Start time (MET in s) [0.0] End time (MET in s) [1800.0] Lower energy limit (TeV) [0.1] Upper energy limit (TeV) [100.0] Calibration database [dummy] Instrument response function [cta_dummy_irf] Model [$CTOOLS/share/models/crab.xml] /Users/jurgen/git/gammalib/test/data/model_point_bplaw.xml Output event data file or observation definition file [events.fits] bplaw.fits
$ ctlike Event list, counts cube or observation definition file [events.fits] bplaw.fits Calibration database [dummy] Instrument response function [cta_dummy_irf] Source model [$CTOOLS/share/models/crab.xml] /Users/jurgen/git/gammalib/test/data/model_point_bplaw.xml Source model output file [crab_results.xml]
which results in the following output (before implementation of the Hessian):
2015-04-10T13:27:59: === GOptimizerLM === 2015-04-10T13:27:59: Optimized function value ..: 3642.268 2015-04-10T13:27:59: Absolute precision ........: 0.005 2015-04-10T13:27:59: Acceptable value decrease .: 2 2015-04-10T13:27:59: Optimization status .......: converged 2015-04-10T13:27:59: Number of parameters ......: 7 2015-04-10T13:27:59: Number of free parameters .: 4 2015-04-10T13:27:59: Number of iterations ......: 12 2015-04-10T13:27:59: Lambda ....................: 0.001 2015-04-10T13:27:59: Maximum log likelihood ....: -3642.268 2015-04-10T13:27:59: Observed events (Nobs) ...: 831.000 2015-04-10T13:27:59: Predicted events (Npred) ..: 830.191 (Nobs - Npred = 0.808691) 2015-04-10T13:27:59: === GModels === 2015-04-10T13:27:59: Number of models ..........: 1 2015-04-10T13:27:59: Number of parameters ......: 7 2015-04-10T13:27:59: === GModelSky === 2015-04-10T13:27:59: Name ......................: Crab 2015-04-10T13:27:59: Instruments ...............: all 2015-04-10T13:27:59: Instrument scale factors ..: unity 2015-04-10T13:27:59: Observation identifiers ...: all 2015-04-10T13:27:59: Model type ................: PointSource 2015-04-10T13:27:59: Model components ..........: "SkyDirFunction" * "BrokenPowerLaw" * "Constant" 2015-04-10T13:27:59: Number of parameters ......: 7 2015-04-10T13:27:59: Number of spatial par's ...: 2 2015-04-10T13:27:59: RA .......................: 83.6331 [-360,360] deg (fixed,scale=1) 2015-04-10T13:27:59: DEC ......................: 22.0145 [-90,90] deg (fixed,scale=1) 2015-04-10T13:27:59: Number of spectral par's ..: 4 2015-04-10T13:27:59: Prefactor ................: 8.86304e-16 +/- 7.48184e-16 [1e-23,1e-13] ph/cm2/s/MeV (free,scale=1e-16,gradient) 2015-04-10T13:27:59: Index1 ...................: -2.33176 +/- 0.180754 [-0,-5] (free,scale=-1,gradient) 2015-04-10T13:27:59: BreakValue ...............: 259124 +/- 84028.9 [10000,1e+09] MeV (free,scale=1e+06,gradient) 2015-04-10T13:27:59: Index2 ...................: -2.73473 +/- 0.0531145 [-0.01,-5] (free,scale=-1,gradient) 2015-04-10T13:27:59: Number of temporal par's ..: 1 2015-04-10T13:27:59: Normalization ............: 1 (relative value) (fixed,scale=1,gradient)
#7
 Updated by Knödlseder Jürgen over 9 years ago
Updated by Knödlseder Jürgen over 9 years ago
- Status changed from New to Feedback
- Assigned To changed from Knödlseder Jürgen to Forest Florent
- % Done changed from 0 to 100
The Hessian computation has been implement as the GObservations::likelihood::hessian method. The implementation is not 100% identical to the Minuit implementation as the
if(fabs((d-dlast)/d) < Tolerstp()) break; if(fabs((g2(i)-g2bfor)/g2(i)) < TolerG2()) break;
conditions have not been implemented.
The code is called from the
GObservations::error_hessian() method which does the inversion of the Hessian matrix.
In the meanwhile we decided however to code a cterror tool for likelihood profile computation. The code is therefore actually not used.
#8
 Updated by Knödlseder Jürgen over 9 years ago
Updated by Knödlseder Jürgen over 9 years ago
Pull distributions have been obtained for all spectral models, results are posted here: https://cta-redmine.irap.omp.eu/projects/gammalib/wiki/Performance_(2015-06)
Only the broken power law pull distributions are incorrect. Add this to the FAQ.
#9
 Updated by Knödlseder Jürgen over 9 years ago
Updated by Knödlseder Jürgen over 9 years ago
- Status changed from Feedback to Closed
- Remaining (hours) set to 0.0
#10
 Updated by Deil Christoph over 9 years ago
Updated by Deil Christoph over 9 years ago
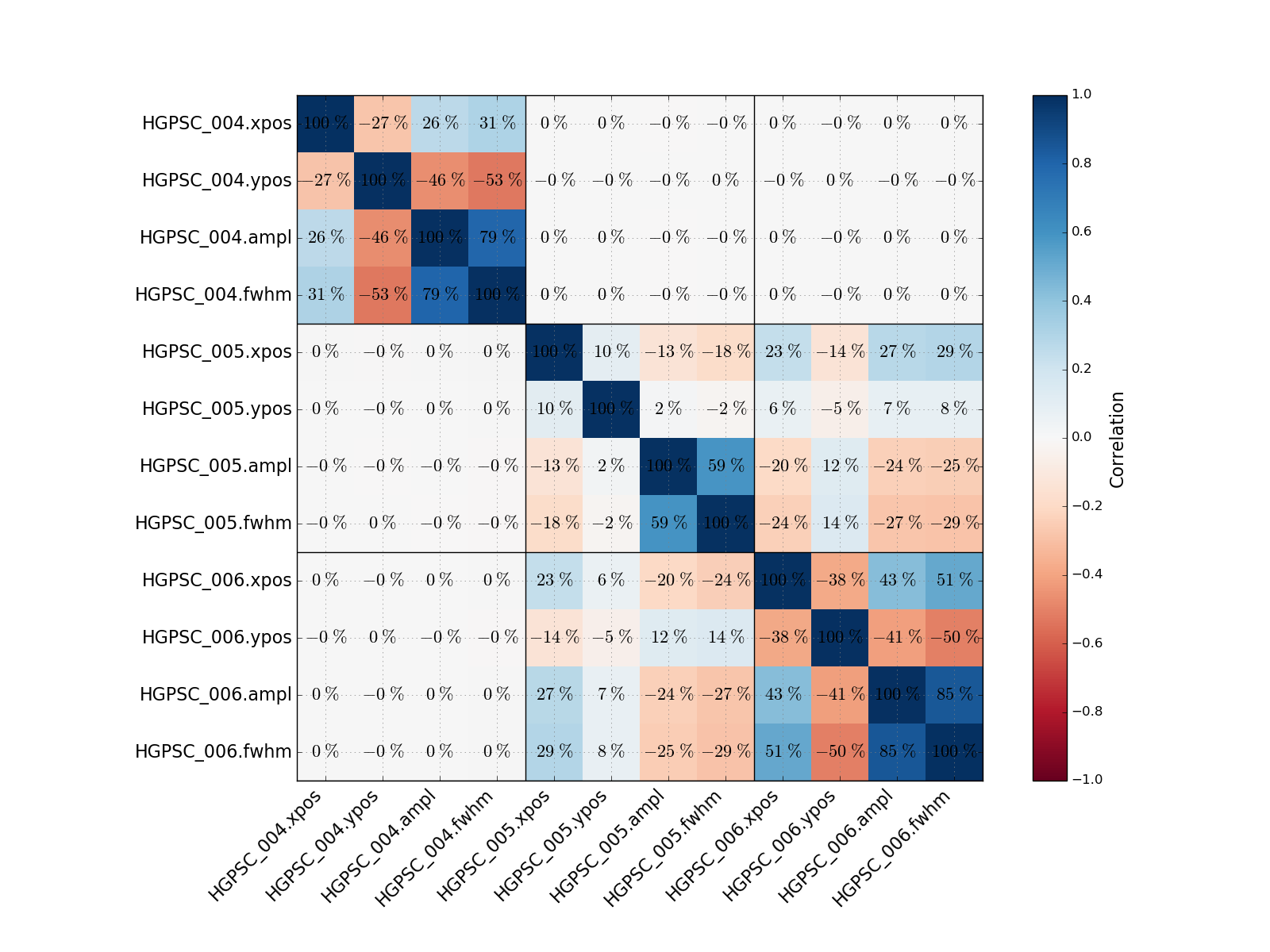
- File GLON_285_correlation_matrix_sherpa.png added
- Estimated time set to 0.00
Attached an example for a plot we use to check parameter correlations ... this is for overlapping Gaussians.
Plotting this matrix and the likelihood profiles with the parabolic approximation is key to debugging issues with the likelihood function and parameter optimisation and error estimation.
Would be great to have these diagnostics plots for ctools as well.
In-scope for ctools or part of a separate package like David’s scripts?
A separate ctool?
#11
 Updated by Knödlseder Jürgen over 9 years ago
Updated by Knödlseder Jürgen over 9 years ago
Here how Minuit is implementing the tolerance condition:
unsigned int Ncycles() const {return fStrategy.HessianNCycles();}
double Tolerstp() const {return fStrategy.HessianStepTolerance();}
double TolerG2() const {return fStrategy.HessianG2Tolerance();}
unsigned int HessianNCycles() const {return fHessNCyc;}
double HessianStepTolerance() const {return fHessTlrStp;}
double HessianG2Tolerance() const {return fHessTlrG2;}
unsigned int HessianGradientNCycles() const {return fHessGradNCyc;}
MnStrategy::MnStrategy(unsigned int stra) {
//user defined strategy (0, 1, >=2)
if(stra == 0) SetLowStrategy();
else if(stra == 1) SetMediumStrategy();
else SetHighStrategy();
}
void MnStrategy::SetLowStrategy() {
// set low strategy (0) values
fStrategy = 0;
SetGradientNCycles(2);
SetGradientStepTolerance(0.5);
SetGradientTolerance(0.1);
SetHessianNCycles(3);
SetHessianStepTolerance(0.5);
SetHessianG2Tolerance(0.1);
SetHessianGradientNCycles(1);
}
void MnStrategy::SetMediumStrategy() {
// set minimum strategy (1) the default
fStrategy = 1;
SetGradientNCycles(3);
SetGradientStepTolerance(0.3);
SetGradientTolerance(0.05);
SetHessianNCycles(5);
SetHessianStepTolerance(0.3);
SetHessianG2Tolerance(0.05);
SetHessianGradientNCycles(2);
}
void MnStrategy::SetHighStrategy() {
// set high strategy (2)
fStrategy = 2;
SetGradientNCycles(5);
SetGradientStepTolerance(0.1);
SetGradientTolerance(0.02);
SetHessianNCycles(7);
SetHessianStepTolerance(0.1);
SetHessianG2Tolerance(0.02);
SetHessianGradientNCycles(6);
}
hence
Tolerstp() = 0.5 / 0.3 / 0.1 TolerG2() = 0.1 / 0.05 / 0.02