Bug #2768
ctbkgcube / Polynom RadialAcceptance
| Status: | New | Start date: | 12/11/2018 | |
|---|---|---|---|---|
| Priority: | High | Due date: | ||
| Assigned To: | - | % Done: | 0% | |
| Category: | - | |||
| Target version: | - | |||
| Duration: |
Description
Hi Jurgen,
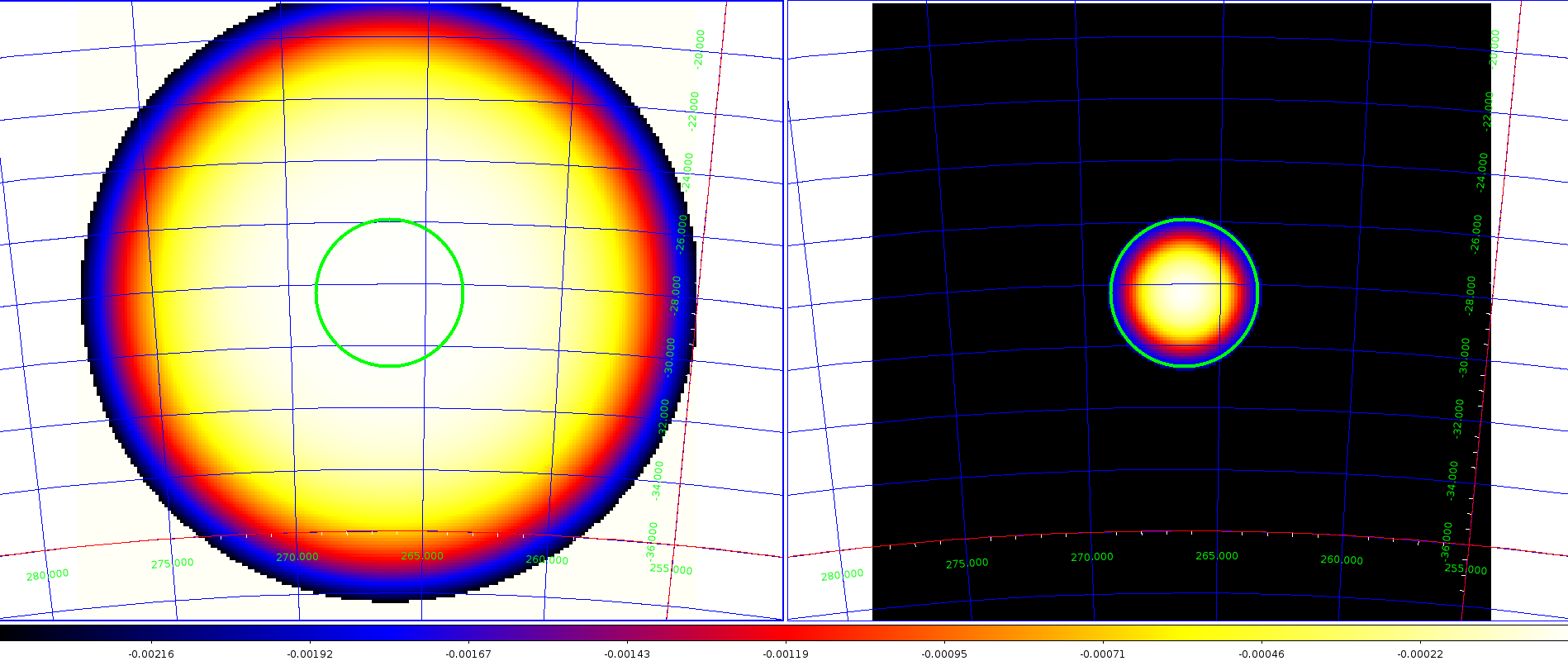
Trying to analyze some data I’ve encountered the following issue. I was needed to model CR residual background as “RadialAcceptance” polynomial function. The region which I’ve tried to analyze contains several observations and thus is significantly broader than the 1 observation (10deg radius vs. 2.5 deg radius for 1 observation). I’ve found, that in this case ctbkgcube produces a file with a lot of negative values located beyond 1 observation radius (please see attached figure, left panel). Subsequently this leads to a weird results produced by ctlike.
In the case if the residual CR background is modeled with CTAAeffBackground this issue is not present, bkgcube is positive and all pixels beyond 1 observation radius are just 0 (right panel of attached figure). The minimal set of files to reproduce the issue is in files.tgz
The reason for this behavior can be that the RadialAcceptance polynomial function formally defined at any distance from the center of observation, but has a physical sense just at distances within 1 observation radius. At larger distances it can take an arbitrary non-zero value. Ctbkgcube might not check that the distance to the center of observation is small enough and just formally calculates the function at all distances for all pixels in the ROI.
May you take a look on this issue, please?
Probably it is possible to introduce one more parameter $\theta_{max}$ to Polynom RadialAceeptance model, such that
$ M(\theta) = \sum c_i \theta^i $ if $\theta < \theta_{max}$ and $M(\theta)=0$ otherwise?
Another option might be to define this $\theta_{max}$ automatically basing on maximal $\theta$ at which effective area is known...
At the moment I can try to overcome this issue by producing bkgcubes for individual observations, re-projecting them to larger ROI and summing together. Is this generally a correct approach?
Recurrence
No recurrence.
History
#1
 Updated by Knödlseder Jürgen over 5 years ago
Updated by Knödlseder Jürgen over 5 years ago
- Priority changed from Normal to High
#2
 Updated by Knödlseder Jürgen over 4 years ago
Updated by Knödlseder Jürgen over 4 years ago
I think the best approach is to clip negative values for the polynomial radial acceptance to zero.