Feature #3973
Implement support for COMPTEL pulsar analysis
| Status: | Closed | Start date: | 01/06/2022 | |
|---|---|---|---|---|
| Priority: | Normal | Due date: | ||
| Assigned To: | % Done: | 100% | ||
| Category: | - | |||
| Target version: | 2.0.0 | |||
| Duration: |
Description
Support should be added to GammaLib to allow for a COMPTEL pulsar analysis.
The following pulsar related tasks existed in COMPASS (I do not have copies of these programs, maybe Werner can provide them):PULBARPulsar Barycentric Time ExtractorPULCCPCreation of PPT in COMPASS format from external list.PULDEITiming analsis on observations of known pulsarsPULDEXPulsar data extractor and phase selectorPULIEXPulsar data extractor and phase selector using GRO clock corrected evPULKD1Kernel Density Estimator analysis for known pulsarsPULLC1Lightcurve modelling in known pulsar analysisPULMLAMultiple Pulsar AnalysisPULPHIPulsar Phase SelectorPULPSLPre-Selection of EVP dataPULSAFSelection and foldingPULSELSelects events for pulsed emission search
A description of the COMPASS pulsar analysis can be found at http://www.helmutsteinle.de/MPE/CBIB/CBIB-articles/Busetta1992.pdf.
The analysis steps comprise:- Time units transformation from UTC to epheremis time
- Evaluation of the components of the GRO_SSB vector using the information on the solar system Barycentre position supplied by the Epheremis
- Evaluation of the light travel time to the solar system Barycentre
- Computation of relativistic delay due to gravitational field of the Sun
This gives a temporal term to be added to UTC time to get the corrected SSB time.
For pulsar epheremis JPL Epheremis at epoch 2000.0 are used.
Recurrence
No recurrence.
History
#1
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
Note that BVC files were produced using BVCGEN and are available in the HEASARC archive. The BVC files contain the CGRO spacecraft (X,Y,Z) position in km with respect to the Sun Barycentre as well as the time delay in seconds (TDELTA column) as function of COMPTEL TJD and TICS. Entries are provided every 131072 tics or 16.384 sec, which is the frequency of a superpacket (i.e. the same frequency as the OAD datasets.
For a given VP all BVC information is in a single file. It’s probably sufficient to implement a GCOMBvc class to deal with the information from the file. Probably the only thing that is really needed is a function that returns the time delay (TDELTA column) as function of COMPTEL TJD and TICS. The question is whether an interpolation of the time delays is needed, which would imply that we need to know to which moment within a superpacket the information corresponds.
#2
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
- Tracker changed from Action to Feature
#3
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
- File 1990_Faihead_A&A_229_240-TT-TB-formula.pdf added
The Barycentric Dynamic Time (TDB) is of relevance for pulsar analysis. Failhead & Bretagnon (1990) give an analytical formula to convert from TT to TDB (they call TBD TB in their paper, see 1990_Faihead_A&A_229_240-TT-TB-formula.pdf). But my guess is that all that is not needed since the time delay is provided in the BVC files. The BVC header states that the TDELTA column contains the time difference TDB-UTC. It seems to be only the ephemeris dependent term (see Busetta et al. 1992). Note that in COMPASS JPL DE200 Ephemeris were used.
Not clear how the source position is folded in here. Probably in the evaluation of the light travel time to the Solar System Barycentre. Pulsar information is provided in COMPASS via the pulsar parameter table (PPT), and Figure 1 of Busetta et al. (1992) shows that BVC and PPT are two inputs to the pulsar analysis.
#4
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
- File 2019_DOrioG_16-10-2019.pdf added
Some information about the use of the pulsar position can be found on https://www.cv.nrao.edu/~sransom/web/Ch6.html.
The Roemer delay ΔR⊙ is the classical light travel time across the Earth’s orbit. Its magnitude is ∼500cosβ s, where β is the ecliptic latitude of the pulsar (the angle between the pulsar and the ecliptic plane containing the Earth’s orbit around the Sun).
According to Equation (1.6) in 2019_DOrioG_16-10-2019.pdf the Roemer delay can be computed using
∆R⊙ = −rob · n / c
where rob is the vector from the observer to the Solar System Barycentre (provided as 3 columns in the BVC file), n is the unit vector from the SSB to the pulsar (which can be computed from the pulsar position) and c is the speed of light.
So the only unknown seems to be the coordinate system of the SSB in the BVC file. The definition of the coordinate system can probably be inferred from the values of the SSB vector itself.
#5
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
- File bvccheck.py
 added
added - Status changed from New to In Progress
- % Done changed from 0 to 10
This little code (bvccheck.py) demonstrates that the BVC file contains a vector going from the SSB to CGRO in celestial coordinates. Inverting the vector (going from CGRO to SSB) results in basically the same celestial position as the Sun, as illustrated in the copy of the screen dump below:
8392:000089536: (-290168044.36,-377463428.32,-163691832.31) 58.1852345 CGRO->SSB( 52.4494, 18.9737) Sun( 52.4094, 18.9607) 8392:000226112: (-290166837.01,-377463955.63,-163692123.04) 58.1852345 CGRO->SSB( 52.4495, 18.9738) Sun( 52.4096, 18.9607) 8392:000357184: (-290165691.11,-377464447.37,-163692400.49) 58.1852345 CGRO->SSB( 52.4497, 18.9738) Sun( 52.4098, 18.9608) 8392:000488256: (-290164551.04,-377464942.43,-163692681.28) 58.1852345 CGRO->SSB( 52.4498, 18.9738) Sun( 52.4100, 18.9608) 8392:000619328: (-290163418.47,-377465439.16,-163692965.39) 58.1852345 CGRO->SSB( 52.4500, 18.9739) Sun( 52.4102, 18.9609) 8392:000750400: (-290162291.74,-377465937.55,-163693252.85) 58.1852345 CGRO->SSB( 52.4501, 18.9739) Sun( 52.4103, 18.9609) 8392:000881472: (-290161171.67,-377466439.27,-163693543.63) 58.1852345 CGRO->SSB( 52.4503, 18.9740) Sun( 52.4105, 18.9609) 8392:001012544: (-290160058.28,-377466942.66,-163693837.75) 58.1852345 CGRO->SSB( 52.4504, 18.9740) Sun( 52.4107, 18.9610) 8392:001143616: (-290158951.55,-377467449.38,-163694135.21) 58.1852344 CGRO->SSB( 52.4505, 18.9740) Sun( 52.4109, 18.9610) 8392:001274688: (-290157850.66,-377467958.60,-163694436.00) 58.1852344 CGRO->SSB( 52.4507, 18.9741) Sun( 52.4111, 18.9611) 8392:001405760: (-290156756.43,-377468471.15,-163694740.12) 58.1852344 CGRO->SSB( 52.4508, 18.9741) Sun( 52.4113, 18.9611) 8392:001536832: (-290155668.04,-377468986.19,-163695047.57) 58.1852344 CGRO->SSB( 52.4510, 18.9742) Sun( 52.4115, 18.9612) ... 8406:689910592: (-178872834.82,-433175315.54,-187866108.92) 58.1849187 CGRO->SSB( 67.5626, 21.8440) Sun( 67.4920, 21.8284) 8406:690041664: (-178871676.76,-433175683.03,-187866522.31) 58.1849187 CGRO->SSB( 67.5628, 21.8441) Sun( 67.4921, 21.8284) 8406:690172736: (-178870523.71,-433176057.19,-187866933.21) 58.1849187 CGRO->SSB( 67.5629, 21.8441) Sun( 67.4923, 21.8285) 8406:690303808: (-178869374.00,-433176438.02,-187867343.27) 58.1849187 CGRO->SSB( 67.5630, 21.8442) Sun( 67.4925, 21.8285) 8406:690434880: (-178868227.62,-433176824.69,-187867751.65) 58.1849187 CGRO->SSB( 67.5632, 21.8442) Sun( 67.4927, 21.8285) 8406:690565952: (-178867085.40,-433177218.85,-187868158.37) 58.1849187 CGRO->SSB( 67.5633, 21.8443) Sun( 67.4929, 21.8285) 8406:690697024: (-178865946.52,-433177618.85,-187868563.42) 58.1849187 CGRO->SSB( 67.5635, 21.8443) Sun( 67.4931, 21.8286) 8406:690828096: (-178864810.97,-433178025.51,-187868965.97) 58.1849187 CGRO->SSB( 67.5636, 21.8444) Sun( 67.4933, 21.8286) 8406:690959168: (-178863678.76,-433178438.84,-187869366.84) 58.1849186 CGRO->SSB( 67.5638, 21.8444) Sun( 67.4935, 21.8286) 8406:691090240: (-178862549.88,-433178859.67,-187869766.05) 58.1849186 CGRO->SSB( 67.5639, 21.8445) Sun( 67.4937, 21.8287) 8406:691188544: (-178861704.68,-433179179.04,-187870063.79) 58.1849186 CGRO->SSB( 67.5640, 21.8445) Sun( 67.4938, 21.8287)
Since the event binning is based on OAD super packet records it would probably be most efficient to implement the same structure also for BVC files, hence a GCOMBvc class for a single record and a GCOMBvcs container class to hold all records. A method should then be added to GCOMBvcs that returns a GCOMBvc record for a given GCOMOad record (using the record time). If no record could be found the method should return a NULL pointer, and the client can then skip the superpacket. In that way, only superpackets with valid BVC information will be used.
const GCOMBvc* GCOMBvcs::operator[](const GCOMOad& oad) const;
The following methods should then be implemented:
GCOMBvc::tdelta(void) const; // Simply return TDELTA member
GCOMBvc::troemer(const GSkyDir& dir) const; // Return Roemer delay as function of sky direction
GCOMBvc::tdelta(const GSkyDir& dir) const; // Return total time delay as function of sky direction
The same logic would then be implemented for the GCOMDri::compute_dre, GCOMDri::compute_drg and GCOMDri::compute_drx methods. Using BVC information would be optional. Here an example of how the code could look like. Note that also some methods need to be added to GCOMObservation to deal with pulsar information. The pulsar information, including the pulsar ephemerides, could be encapsulated in a dedicated GPulsar class. This needs probably first a better understanding of how pulsar ephemerides information is structured.
// Get reference to Orbit Aspect Data of superpacket
const GCOMOad &oad = obs.oads()[i_oad];
// Check superpacket usage
if (!use_superpacket(oad, obs.tim(), select)) {
continue;
}
// Optionally get time difference for pulsar
double tdelta = 0.0;
GCOMBvc* bvc = NULL;
if (obs.has_pulsar()) {
bvc = obs.bvcs().find(oad);
if (bcv == NULL) {
continue;
}
tdelta = bvc->tdelta(obs.puldir());
}
#6
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
Here an interesting note on pulsar ephemerides in the CGRO epoch: https://www.jb.man.ac.uk/~pulsar/crab/CGRO_format.html.
After much discussion of the issues, Dick Manchester and I have settled on a specific format for data files containing the information you'll need. Most of the essential information will be in a file called "psrtime.dat", available by anonymous ftp from puppsr.princeton.edu (or Internet address 128.112.128.165). After you login with username "anonymous" and using anything for a password, type "cd gro" to change to the GRO directory. Then you can "get psrtime.dat" to download the main data file. A copy of this message (or suitably updated instructions) will be available as the file "read.me", and the file containing binary pulsar data is "psrbin.dat".
A short dummy version of the main file looks like this (you'll have
to list it on a wide or "landscape mode" (120 column) printer to
see the full width):
PSR B RA(J2000) DEC(J2000) MJD1 MJD2 t0geo(MJD)
f0(s^-1) f1(s^-2) f2(s^-3) RMS O B
-------------------------------------------------------------------------
----------------------------------------
0531+21 05 34 31.974 22 00 52.05 48282 48316 48299.000000134
29.9516010684378 -3.77726D-10 0.00D+00 5.5 P
0655+64 07 00 37.811 64 18 11.26 44546 47829 46187.000002101
5.1106207921632 -1.76088D-17 0.00D+00 0.7 P *
0833-45 08 35 20.680 -45 10 35.70 48256 48320 48288.000000968
11.1989616062225 -1.55846D-11 1.08D-21 0.5 P
1855+09 18 57 36.394 09 43 17.33 46437 48239 47338.000000045
186.4940816803072 -6.20316D-16 0.00D+00 0.2 P *
The column headings should be reasonably self-explanatory:
PSR Pulsar name in 1950 coordinates (for consistency with prior usage)
RA Right Ascension in J2000 coordinates (hh mm ss.sss)
DEC Declination in J2000 coordinates (sdd mm ss.ss)
MJD1,2 First and last dates for valid parameters (MJD)
t0geo Infinite-frequency geocentric UTC arrival time of a pulse (MJD)
Note: the integer part of t0geo is the barycentric (TDB) epoch
of RA, DEC, f0, f1,and f2
f0 Pulsar rotation frequency (s**(-1))
f1 First derivative of pulsar frequency (s**(-2))
f2 Second derivative of pulsar frequency (s**(-3))
RMS Root-mean-square radio timing residual, in milliperiods
O Observer code
B Blank for single pulsars, "*" for binaries.
The "Observer codes" have the following meanings and contact persons:
A Australia Telescope National Facility (Dick Manchester)
B Bologna (Nichi D'Amico)
C Cornell/Carleton (Jim Cordes, Joel Weisberg)
J Jodrell Bank (Andrew Lyne)
P Princeton (Joe Taylor)
For binary pulsars, the orbital parameters will be put in a file
called "psrbin.dat". A short dummy version of the file looks like this:
PSR B pb a1*sin(i) e t0 omega
omdot gamma pbdot O
-------------------------------------------------------------------------
-------------------------------
0655+64 88877.061781 4.1255679 0.00000000 46386.41030392
180.000000 0.00000 0.000000 0.00D+00 P
1855+09 1065067.590793 9.2307810 0.00002157 47529.90001480
276.493717 0.00000 0.000000 0.00D+00 P
where the parameter definitions are (for details, see Taylor and
Weisberg,=20
Astrophys. J. 345, 434, 1989):
PSR Pulsar name
pb Orbital period (s)
a1sini Projected semi-major axis (light seconds)
e orbital eccentricity
t0 Barycentric time (TDB scale) of periastron (MJD)
omega Longitude of periastron (degrees)
omdot First derivative of omdot (degrees per Julian year)
gamma Time-dilation and gravitational redshift parameter (s)
pbdot First derivative of pb
O Observer code
Many binary pulsars will not require the last three (relativistic)
parameters.
Finally, a word for programmers. The Fortran statements used to
write out the file entries are listed below:
Main file:
write(33,1120) psrname,irh,irm,rsec,decsgn,idd,idm,dsec,
+ mjd1,mjd2,t0geo,f0,f1,f2,rmsmp,obsflag,binflag
1120 format(a8,2i3.2,f7.3,1x,a1,i2.2,i3.2,f6.2,2i6,f16.9,
+ f18.13,1p,d13.5,d11.2,0p,f5.1,2(1x,a1))
Binary pulsar file:
write(34,1100) psrname,pb,a1,e,t0mjd,omz,omdot,gamma,pbdot,
+ obsflag
1100 format(a8,f17.6,f12.7,f11.8,f15.8,f11.6,f8.5,f9.6,
+ 1p,d11.2,0p,1x,a1)
#7
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
- File all.gro.txt
 added
added
The Crab ephemerides in the format described above for the CGRO period could be found at http://www.jb.man.ac.uk/~pulsar/crab.html. The file is here all.gro.txt.
The website says: If you make use of these data in a publication, we request that you acknowledge the source of the information by referencing the paper: Lyne, A. G., Pritchard, R. S. & Graham-Smith, F. 1993. MNRAS, 265, 1003, which describes the origin of the data, and by quoting the web address http://www.jb.man.ac.uk/~pulsar/crab.html.
This should be all we need to dance!
#8
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
- % Done changed from 10 to 30
Initial versions of the classes GCOMBvc and GCOMBvcs were added that support reading of COMPASS BVC files. The GCOMBvc::tdelta() method is also already implemented, and some unit tests are added.
#9
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
Note that it appears that the BVC times are the mid-point of the corresponding superpacket. For that reason I modified the GCOMBvc class so that it simply returns the time instead of the start and stop times.
#10
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
See also this good reference for the computations to do: https://asd.gsfc.nasa.gov/Craig.Markwardt/bary/.
#11
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
- File tdelta_10000steps.png added
- File tdelta_100000steps.png added
- File tdelta_zoom_start.png added
- % Done changed from 30 to 40
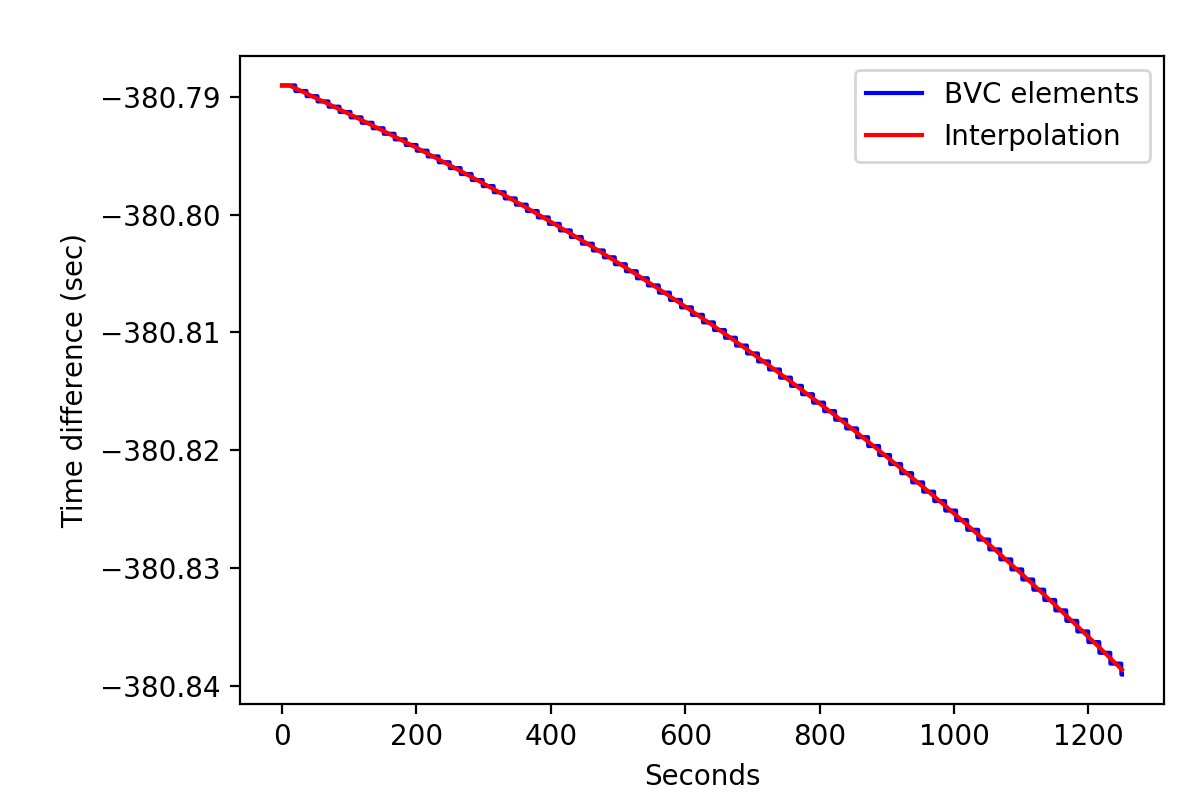
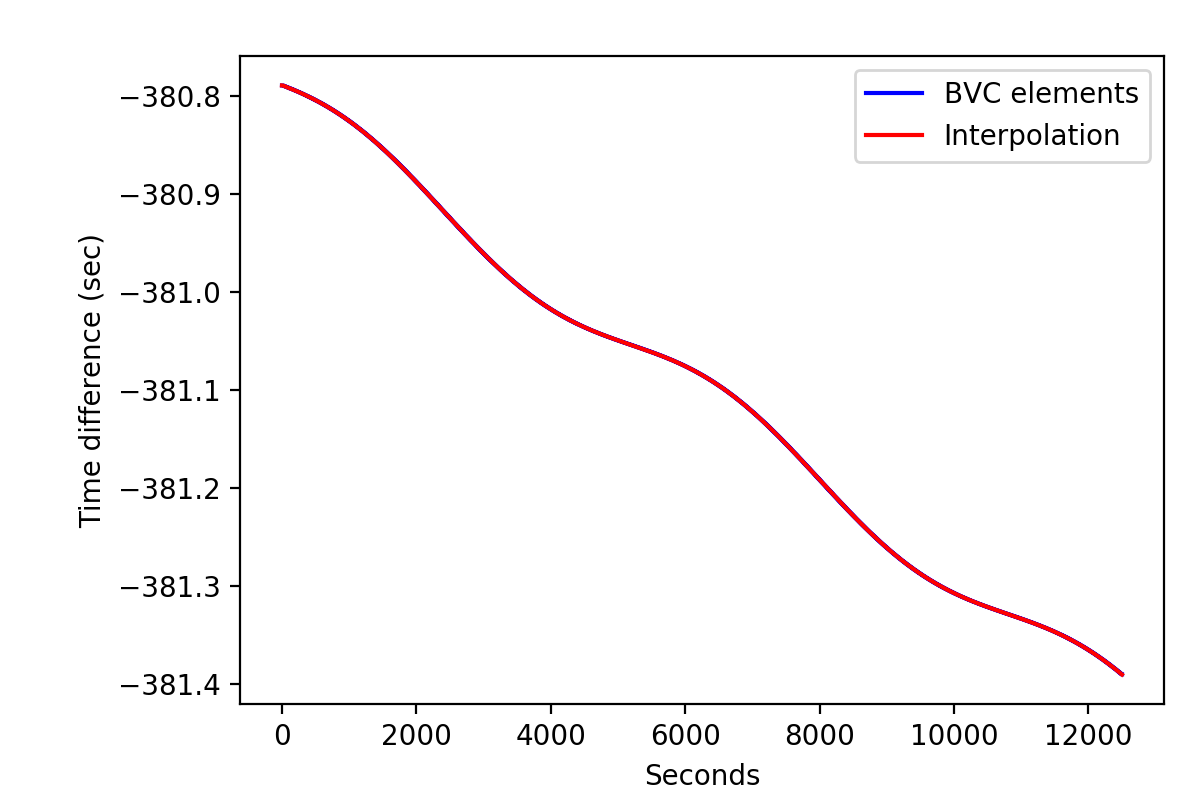
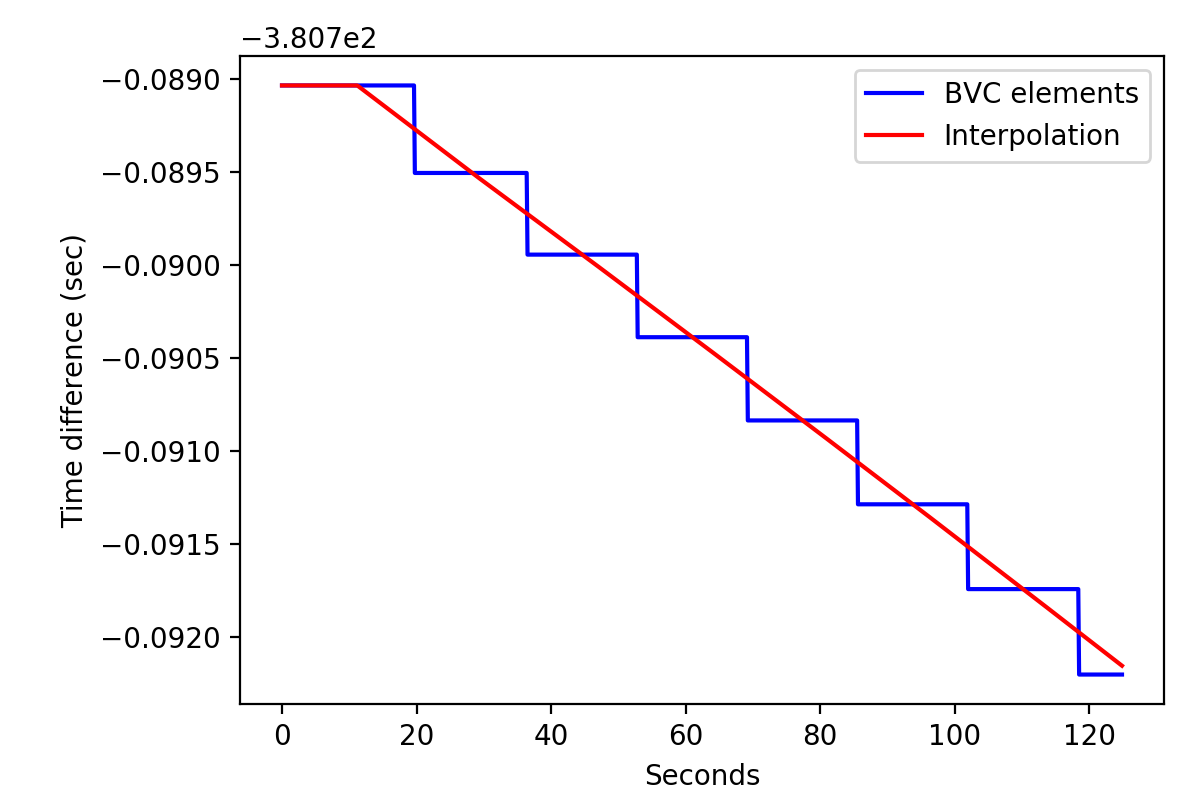
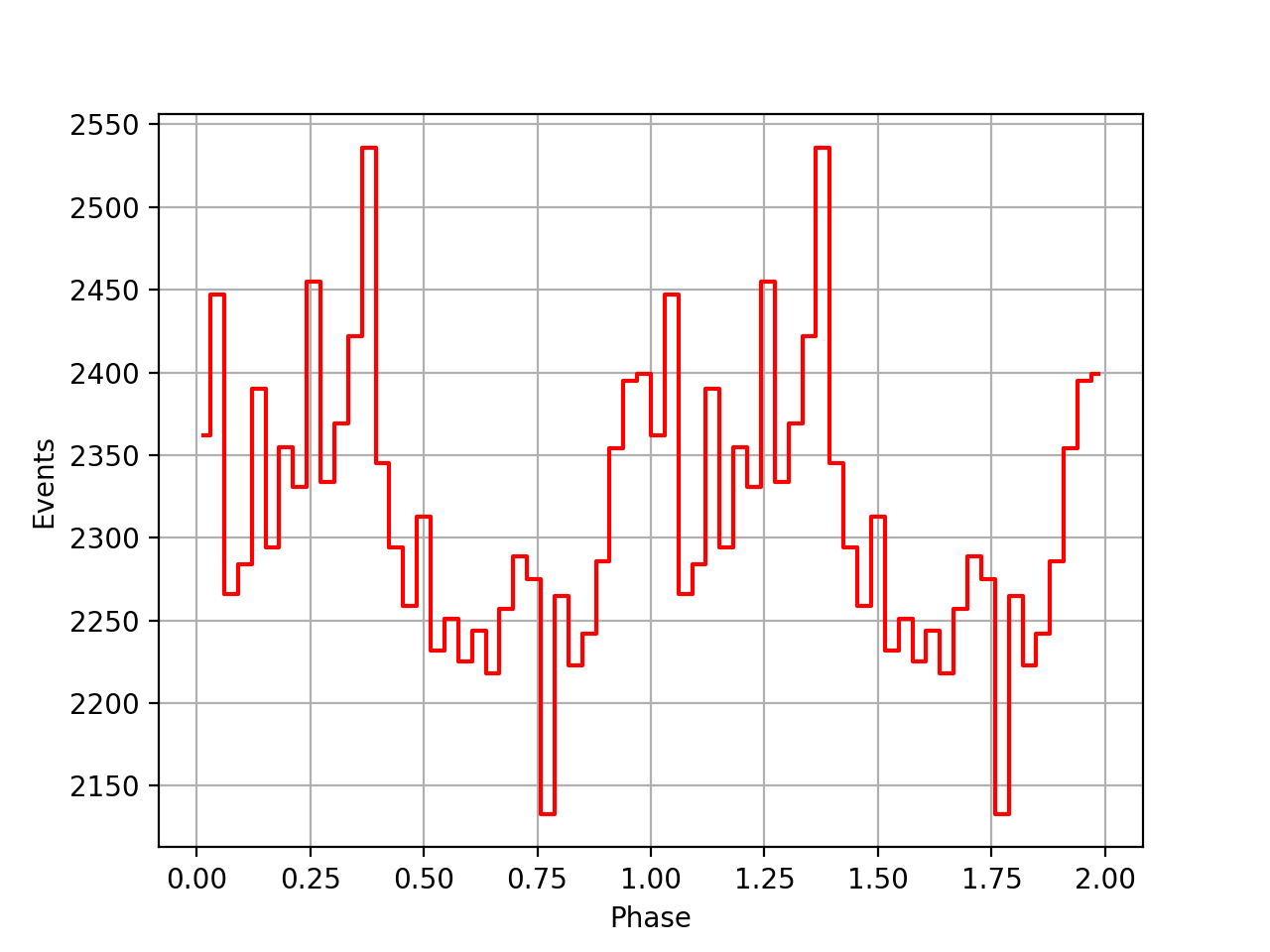
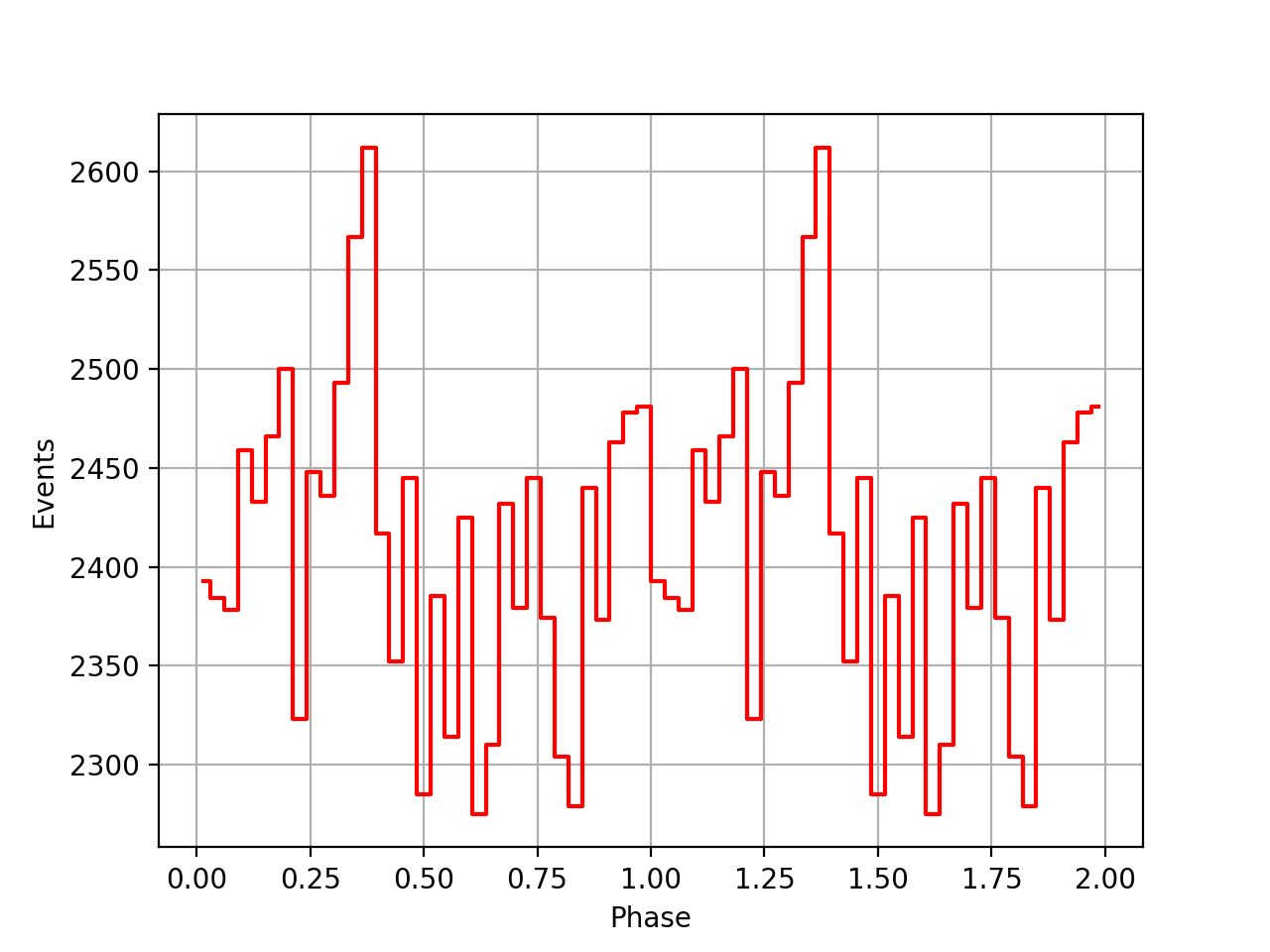
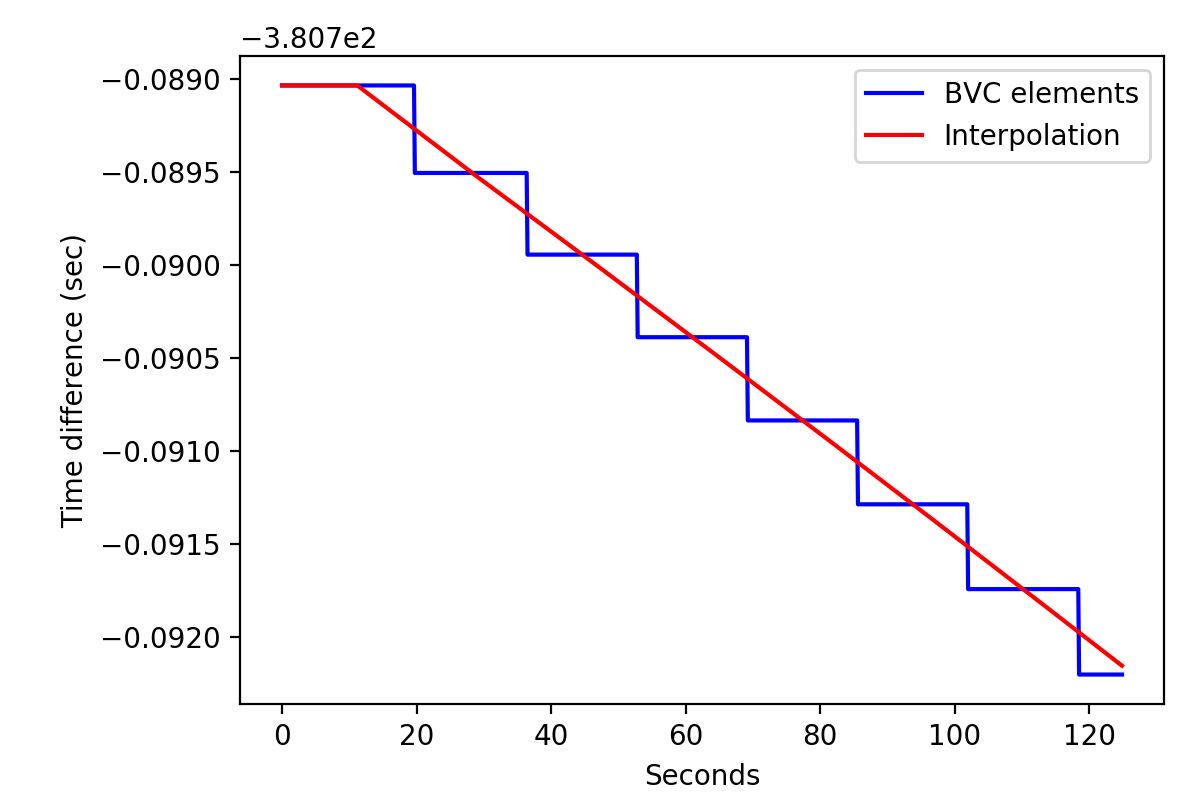
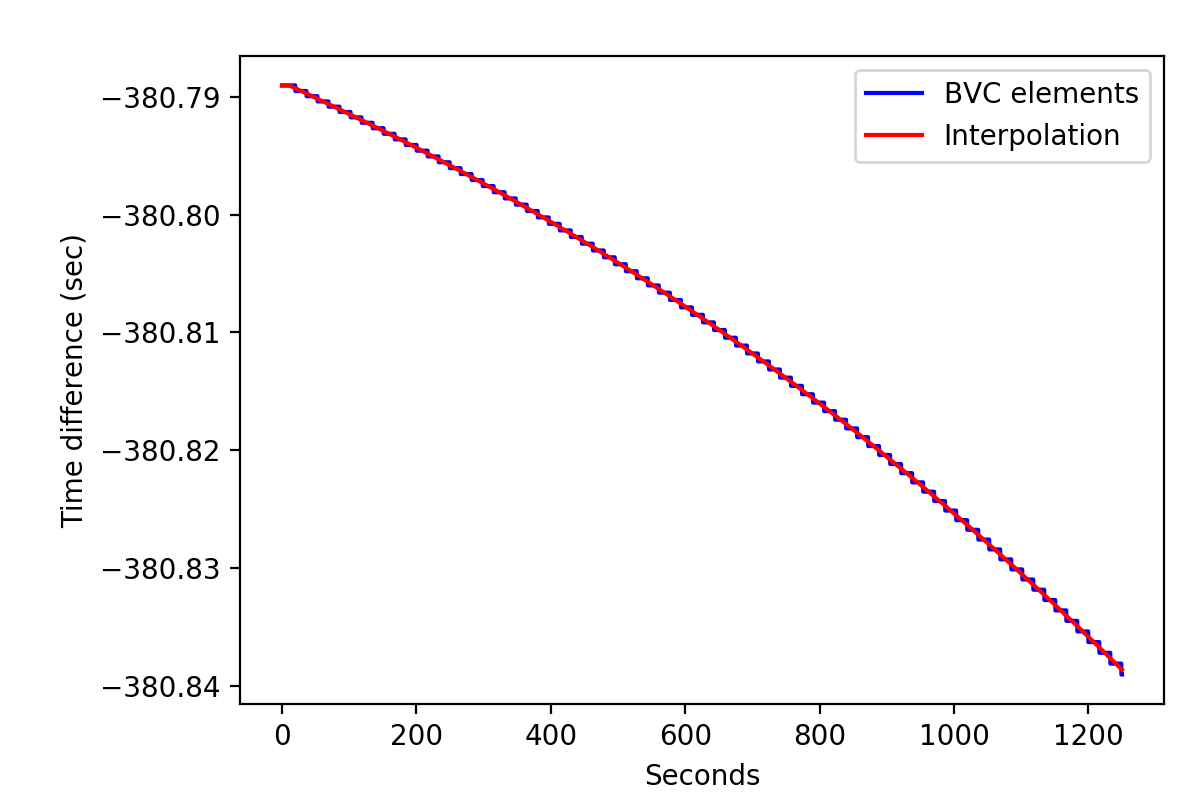
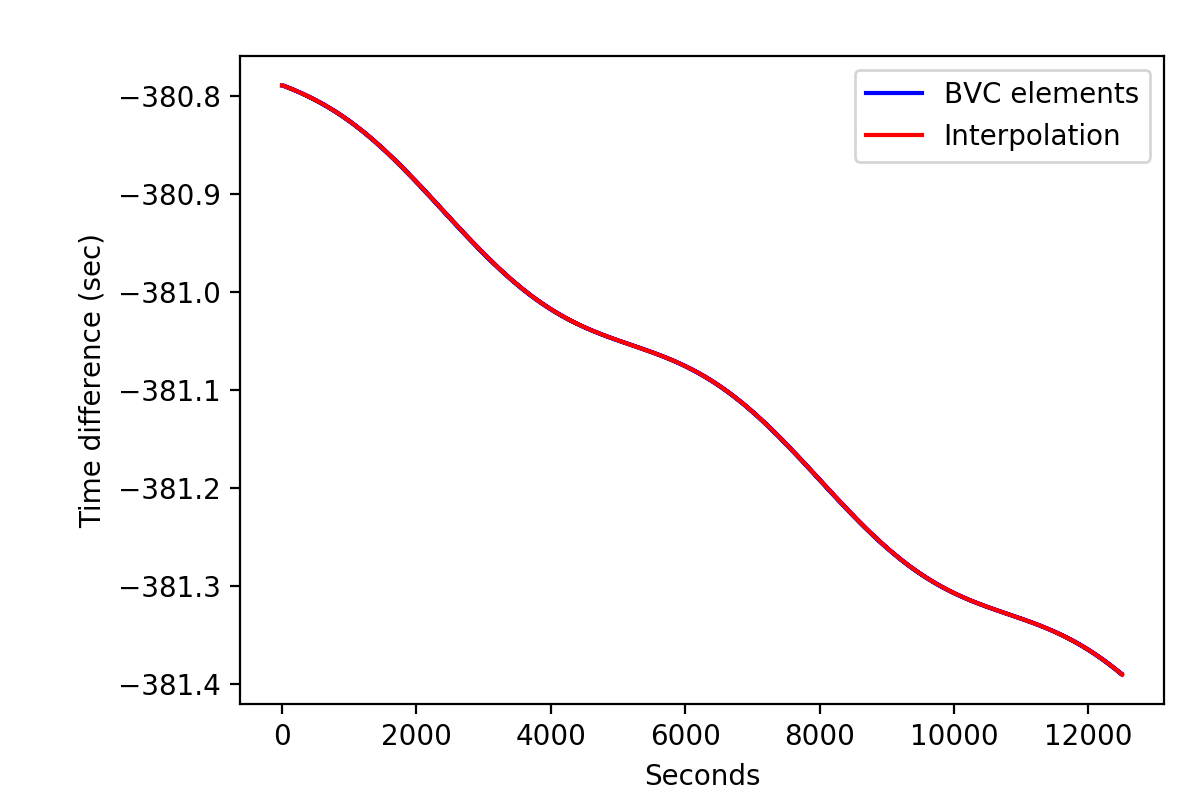
I further implemented the GCOMBvcs::tdelta(GSkyDir, GTime) method that performs a linear interpolation of the SSB vector and the time difference provided in the BVC file. The figures below show the use of a single BVC element for a given superpacket (blue) and a linear interpolation of the BVC information using the new method for the Crab pulsar. The typical step in the time difference for the blue curve is 0.5 ms, which can be problematic for fast spinning pulsars. Hence the linear interpolation scheme is to be preferred.
Note in the first image the flattening of the red curve which comes from the times that are earlier than the first time in the BVC file. Eventually, an extrapolation could be put in place. Note also the wiggling in the right image which comes from CGRO orbiting the Earth.
 |
 |
 |
#12
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
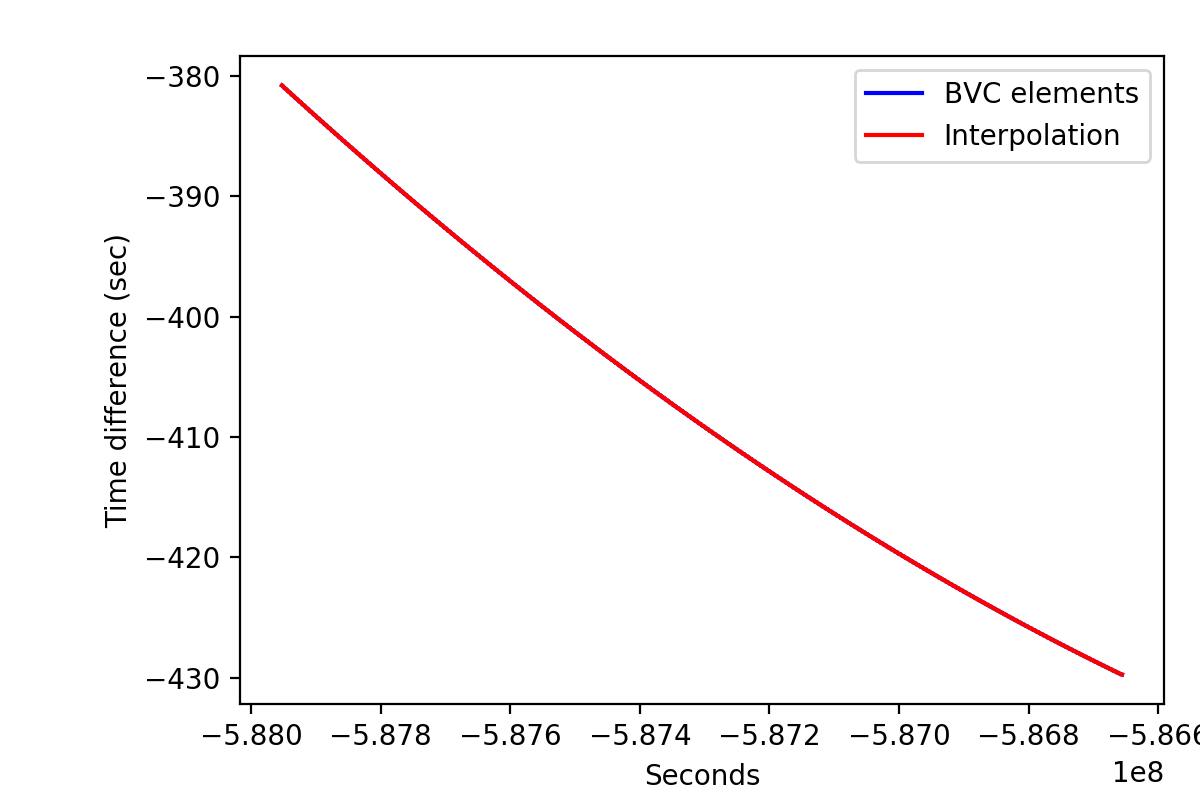
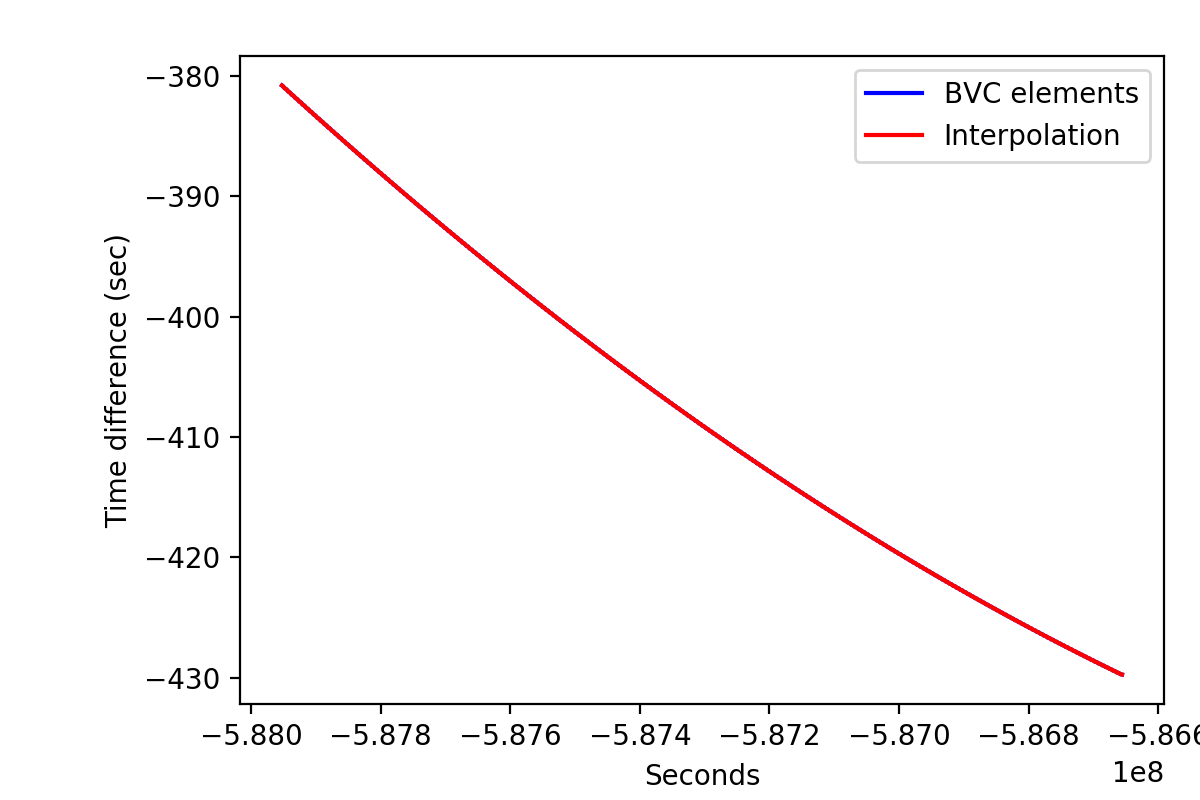
- File tdelta_vp0001.png added
Here the result for the full interval of VP 0001 and the Crab.
#13
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
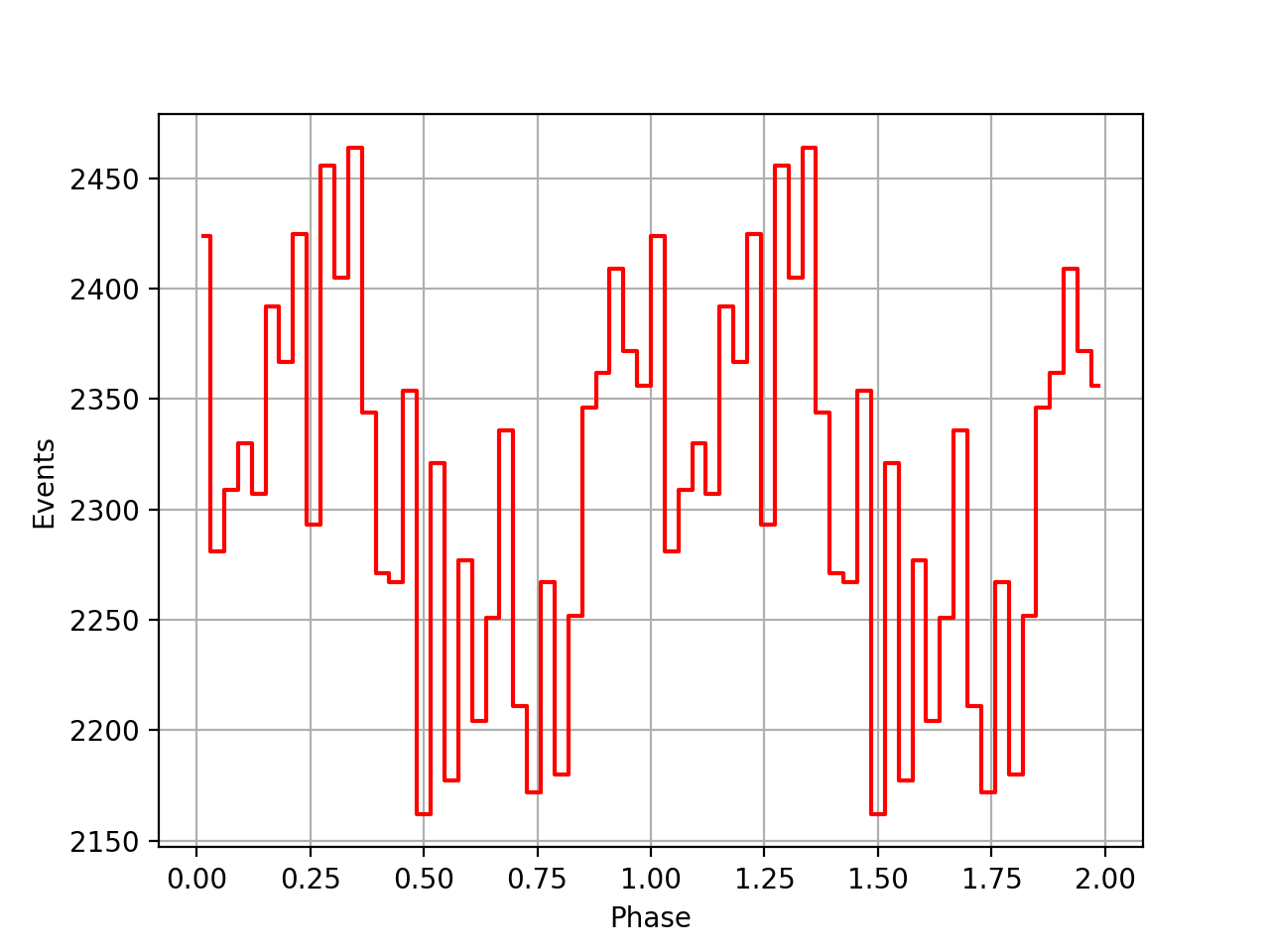
- File pulsar.png added
- % Done changed from 40 to 50
I finalised with the full implementation of the pulsar phase computation and selection in CGOMDri::compute_dre().
I added a GPulsar class that collects ephemerides for a given pulsar. The ephemerides are implemented by the GPulsarEphemeris class. The GPulsar class supports reading ephemerides in various formats, including the psrtime format, the INTEGRAL and Fermi format and tempo2 par files.
The GCOMSelection class now has a GPulsar member and also holds a GPhases member for pulsar phase.
At the beginning of CGOMDri::compute_dre() I added some code that limits the Good Time Interval to the ephemerides validity periods, assuring thus that only events will be handled that have times with ephemerides information. The same code was added to CGOMDri::compute_drg() and CGOMDri::compute_drx(), assuring that the resulting DRIs are consistent.
// Get Good Time Intervals and if a pulsar is specified then reduce
// them according to the validity of the pulsar emphemerides. Throw
// an exception if a pulsar is specified but no BVC data is present.
GCOMTim tim = obs.tim();
bool has_pulsar = false;
if (m_selection.has_pulsar()) {
if (!obs.bvcs().is_empty()) {
tim.reduce(m_selection.pulsar().validity());
m_gti.reduce(m_selection.pulsar().validity());
has_pulsar = true;
m_phasecor = m_selection.pulsar_phases().length();
}
else {
std::string msg = "Phase selection for pulsar \""+
m_selection.pulsar().name()+"\" specified but no "
"BVC data found for observation. Please specify an "
"observation that contains BVC data.";
throw GException::invalid_value(G_COMPUTE_DRE, msg);
}
}
Here the pulse phase selection code in CGOMDri::compute_dre():
// Optionally apply pulsar phase selection
if (has_pulsar) {
// Get pulsar ephemeris
const GPulsarEphemeris& ephemeris =
m_selection.pulsar().ephemeris(event->time());
// Convert time to Solar System Barycentre
GTime time = event->time() +
obs.bvcs().tdelta(ephemeris.dir(), event->time());
// Compute pulsar phase
double phase = ephemeris.phase(time);
// If phase is not contained in phase interval then skip event
if (!m_selection.pulsar_phases().contains(phase)) {
continue;
}
} // endif: applied pulsar selection
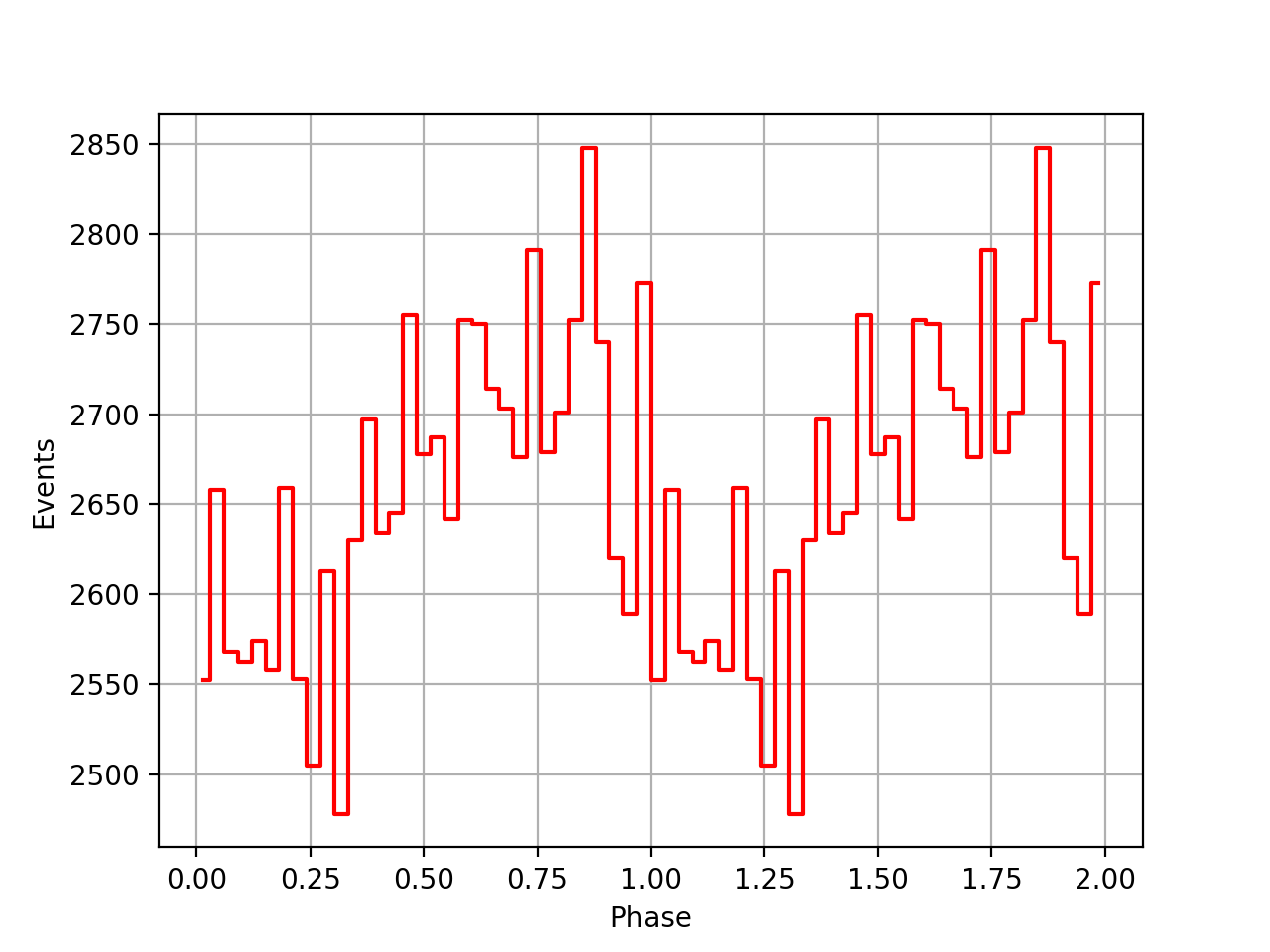
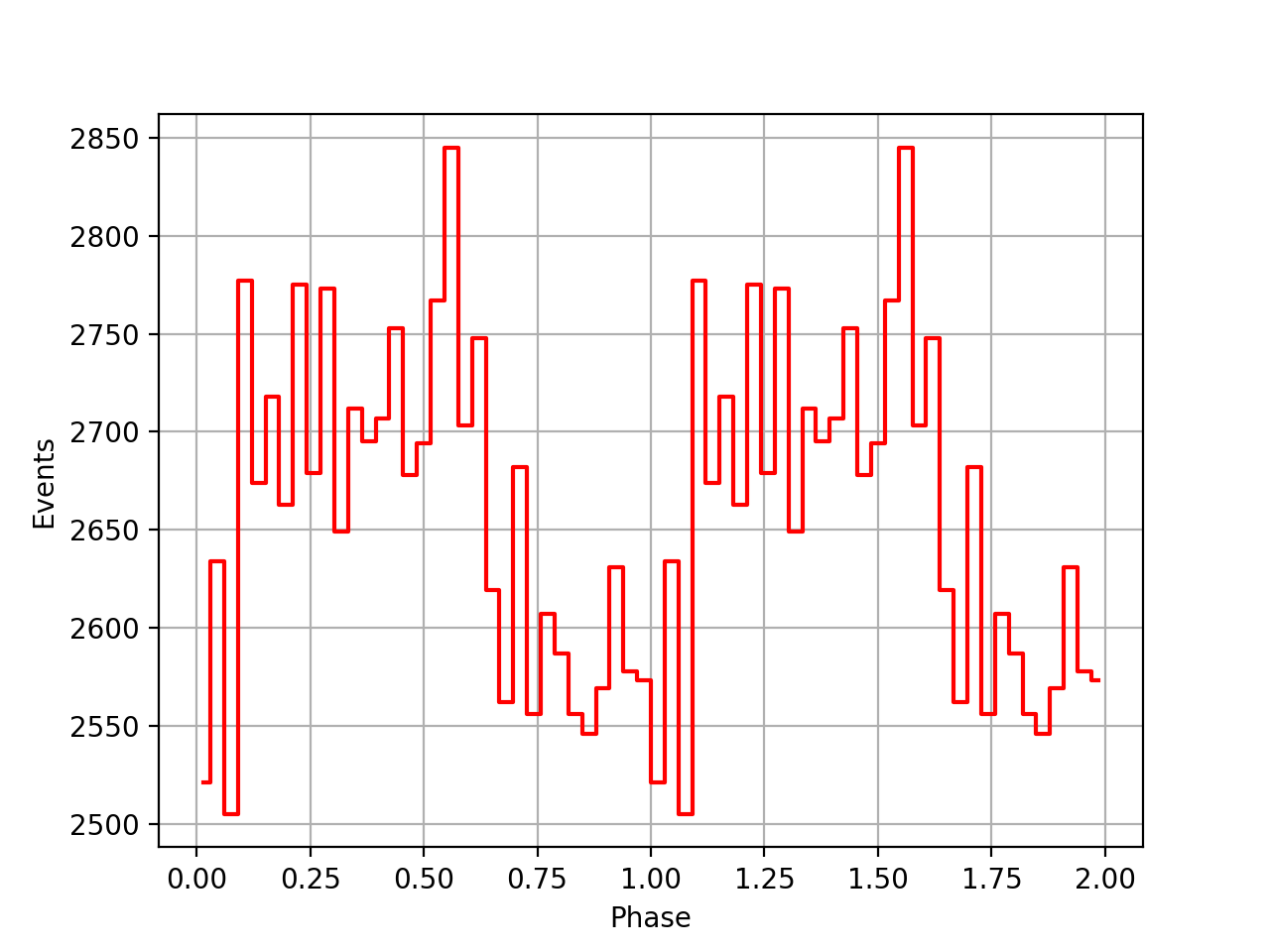
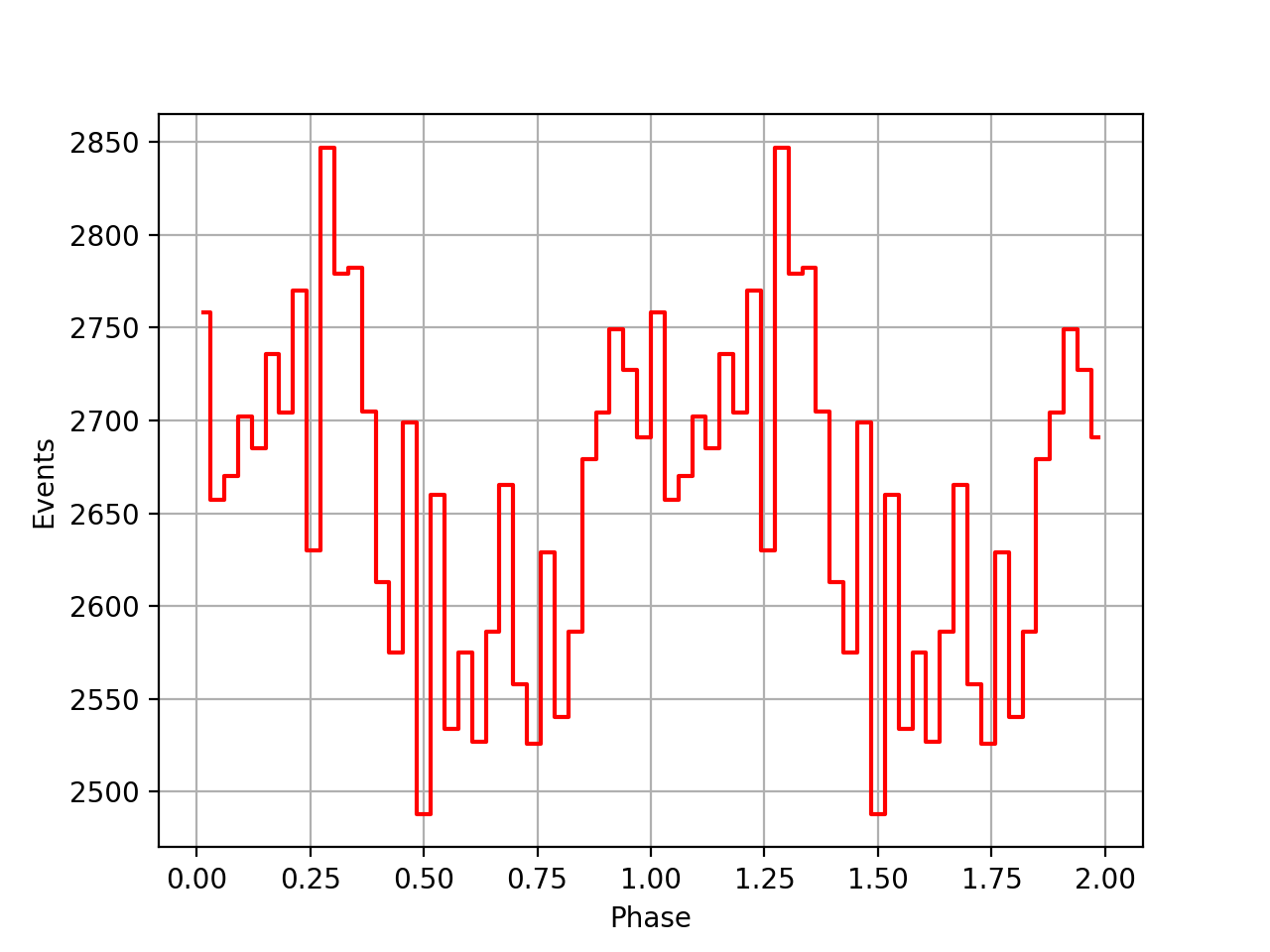
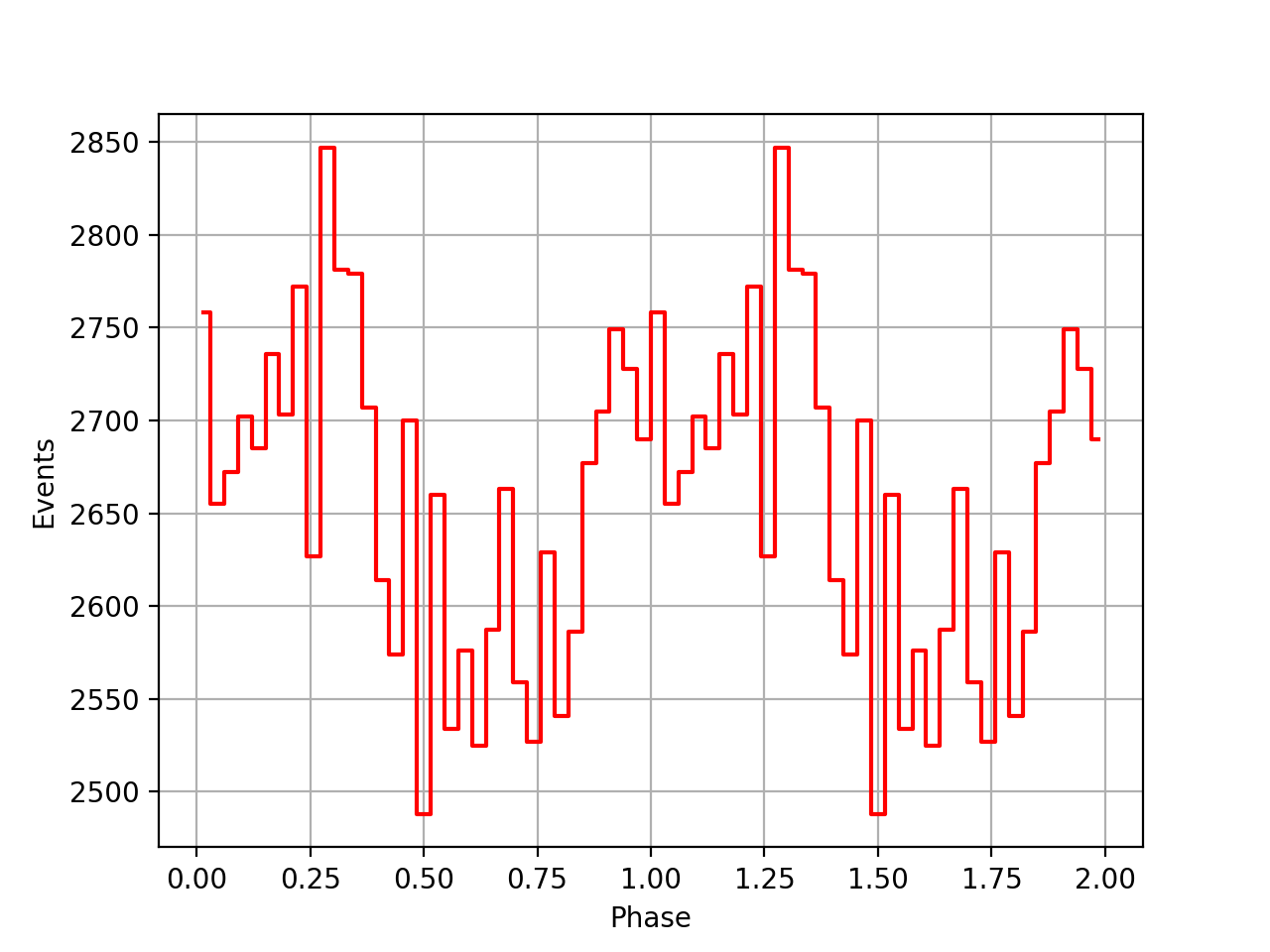
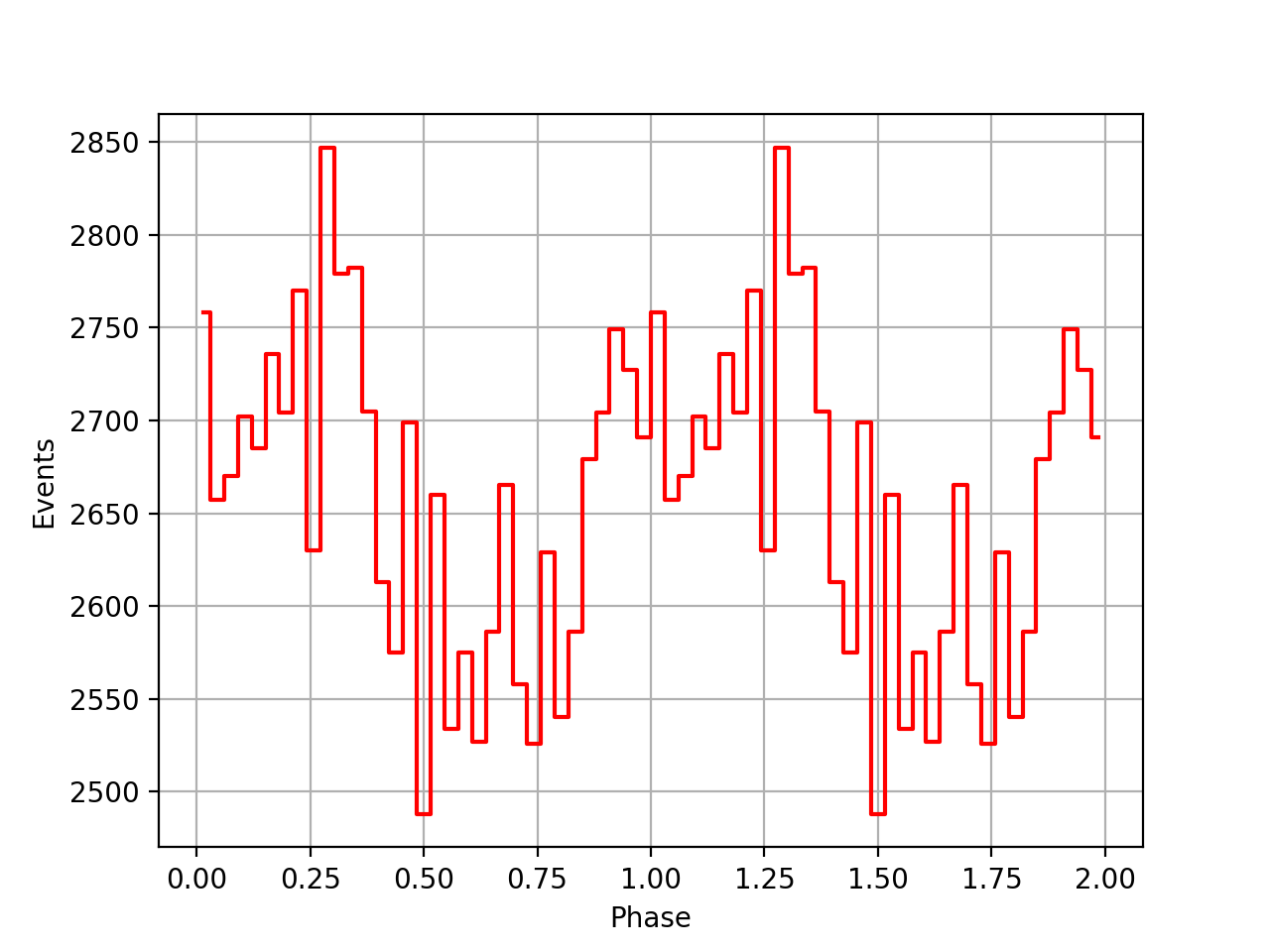
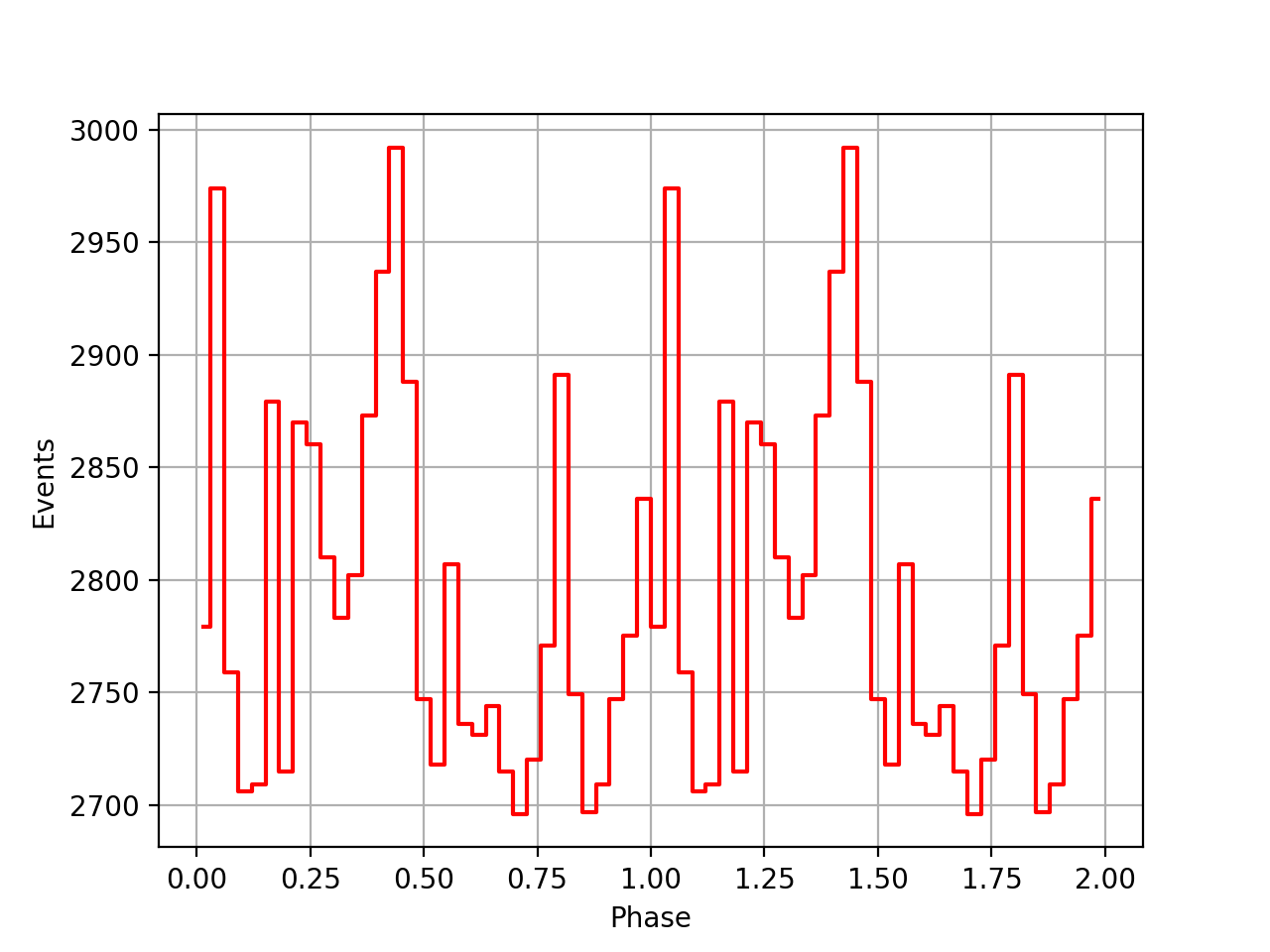
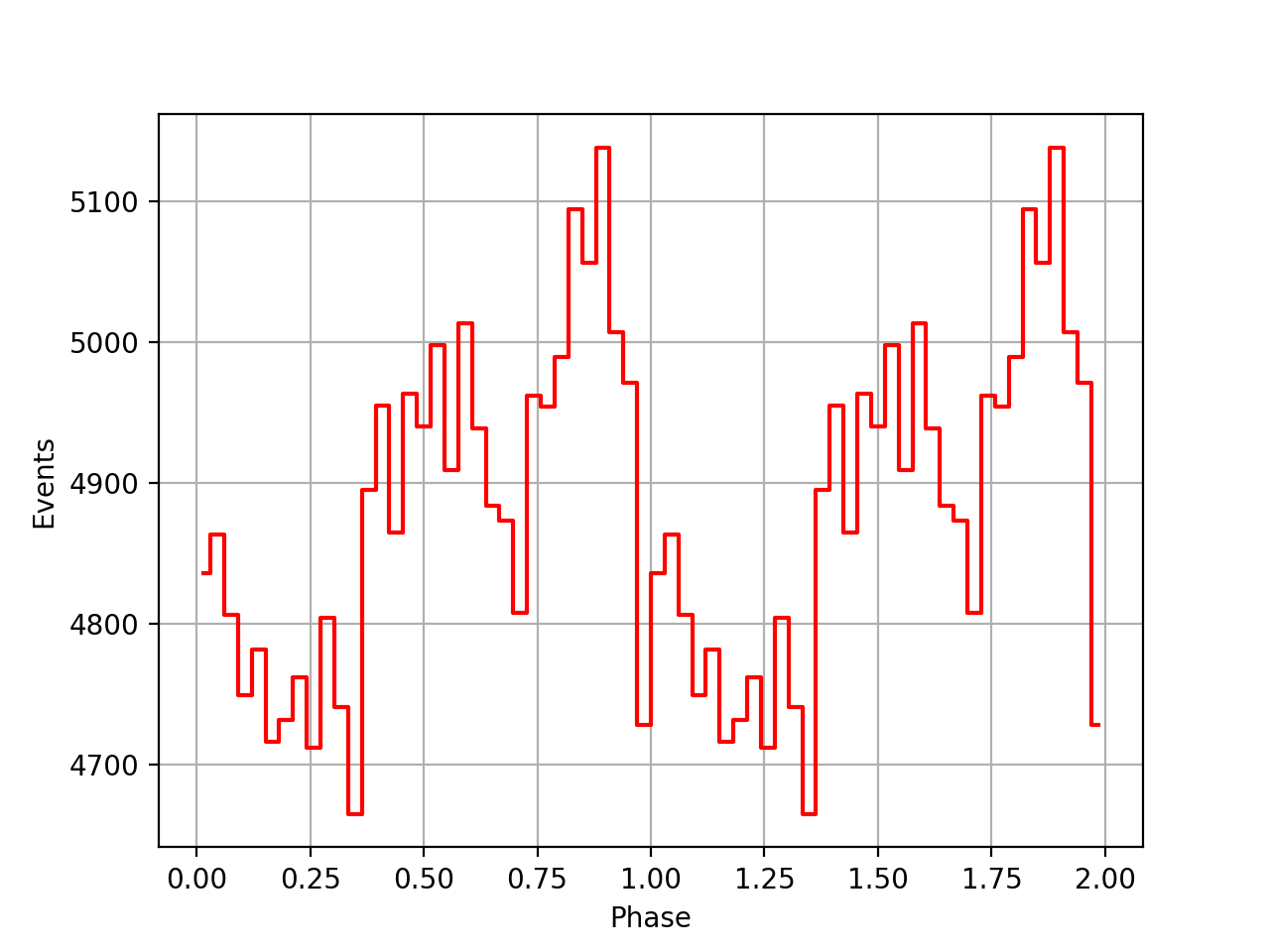
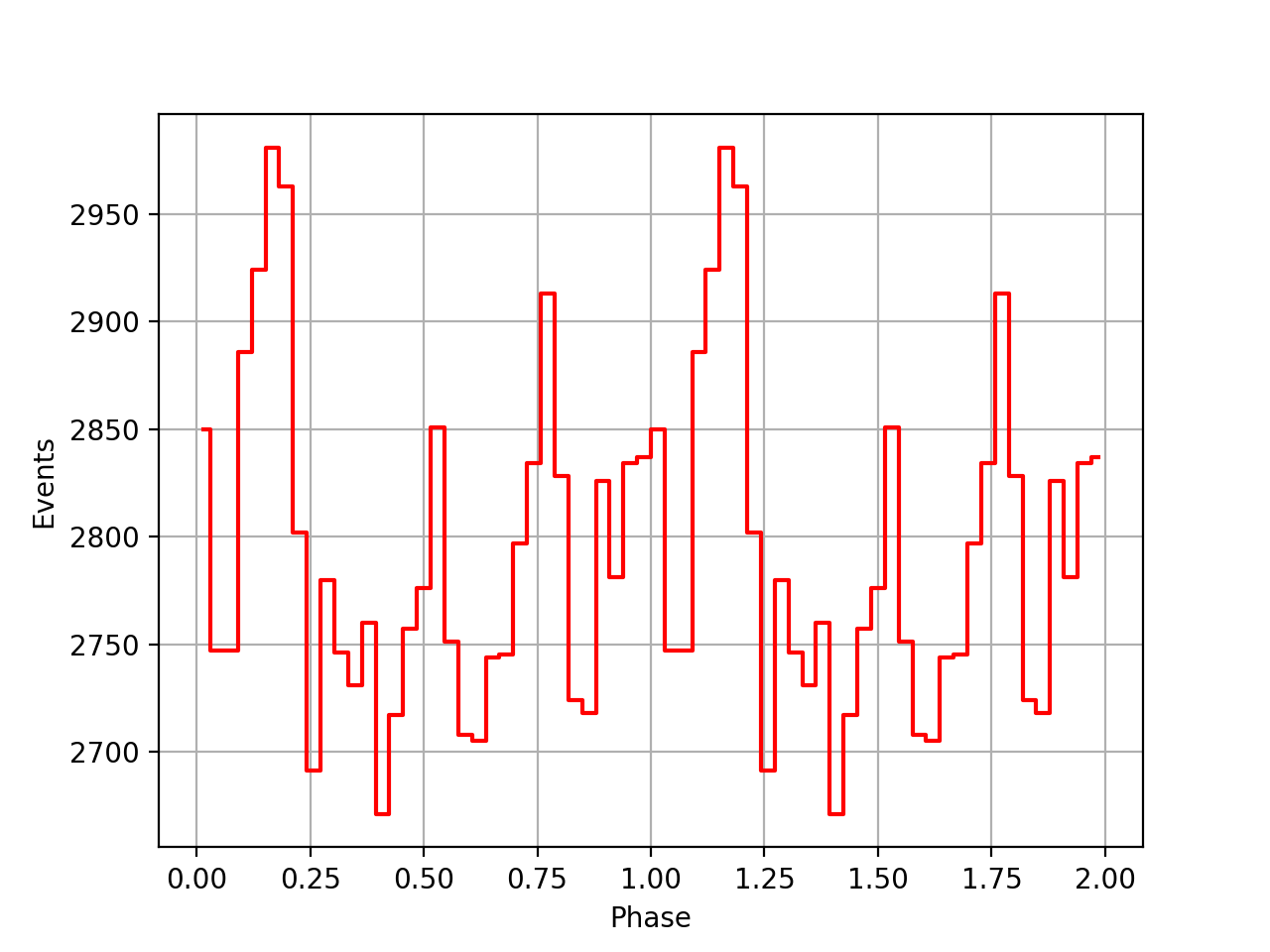
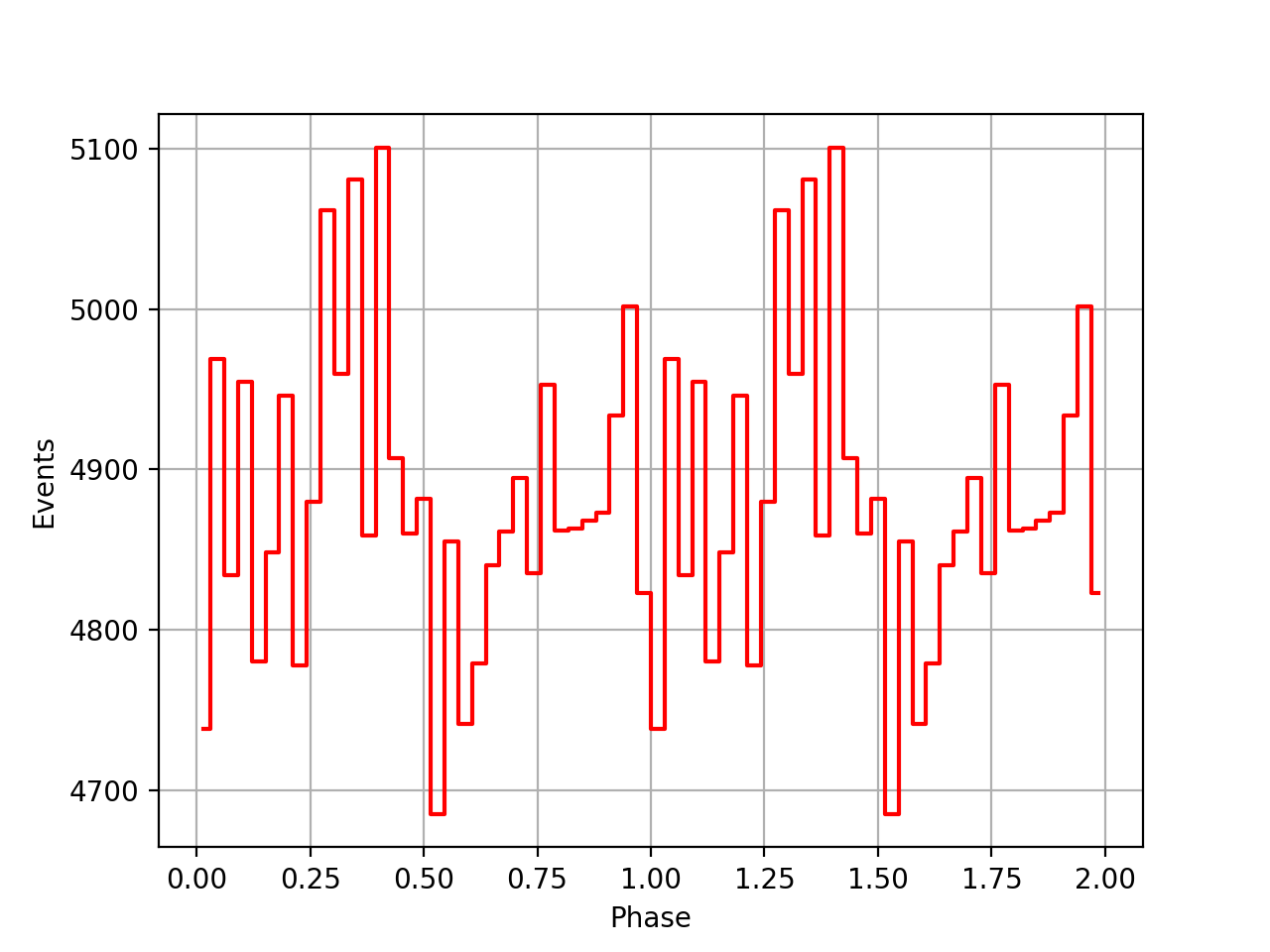
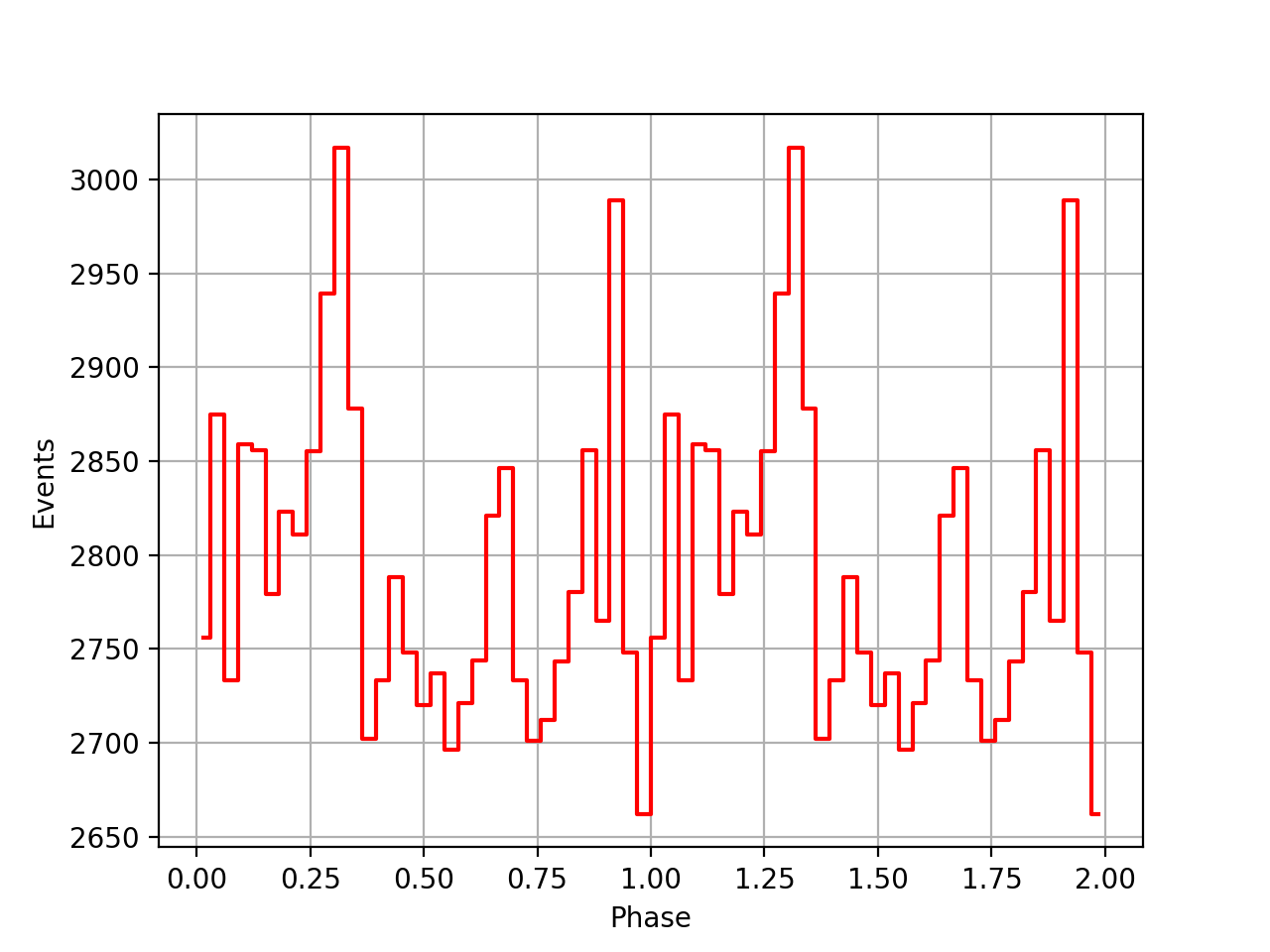
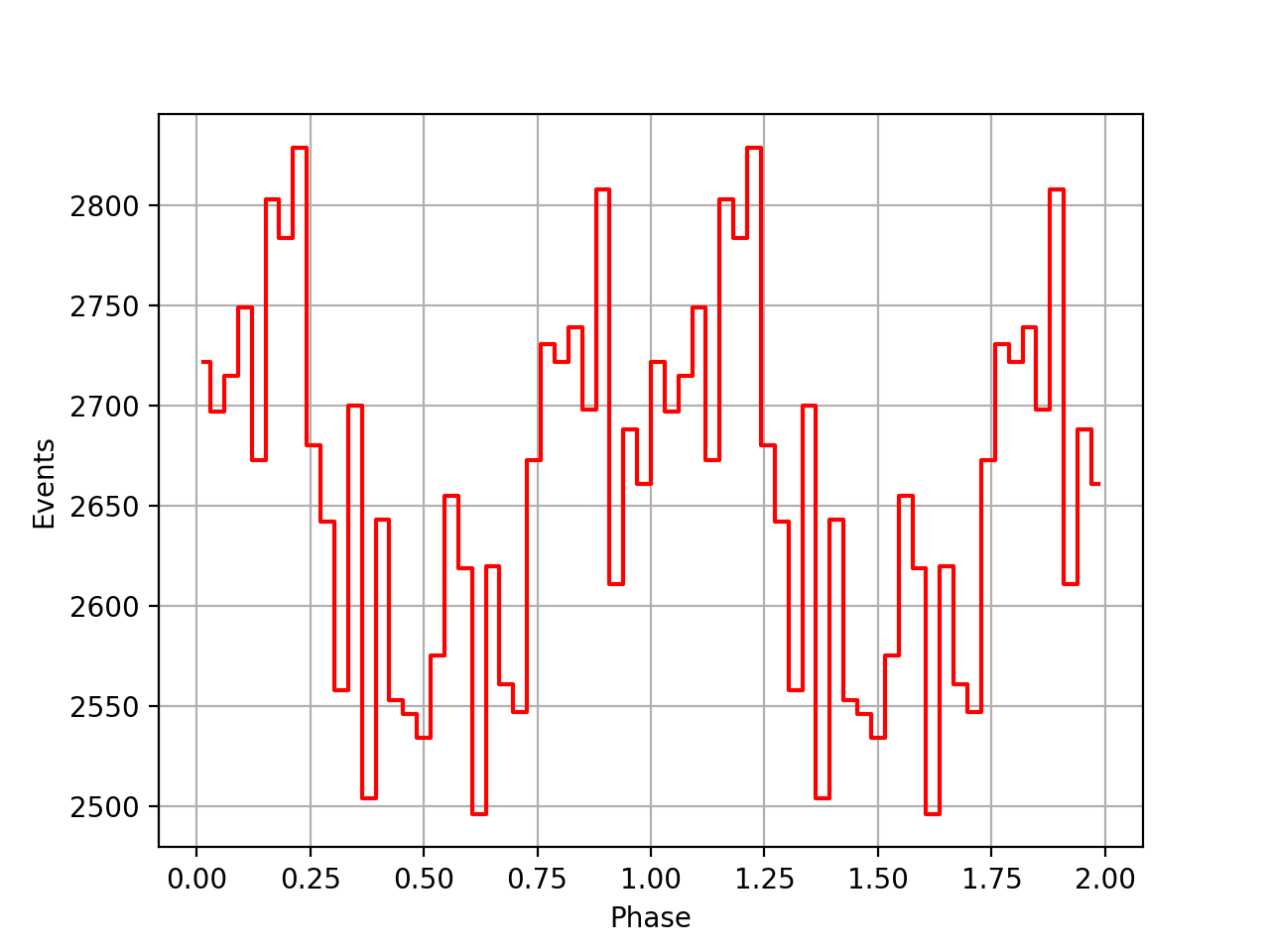
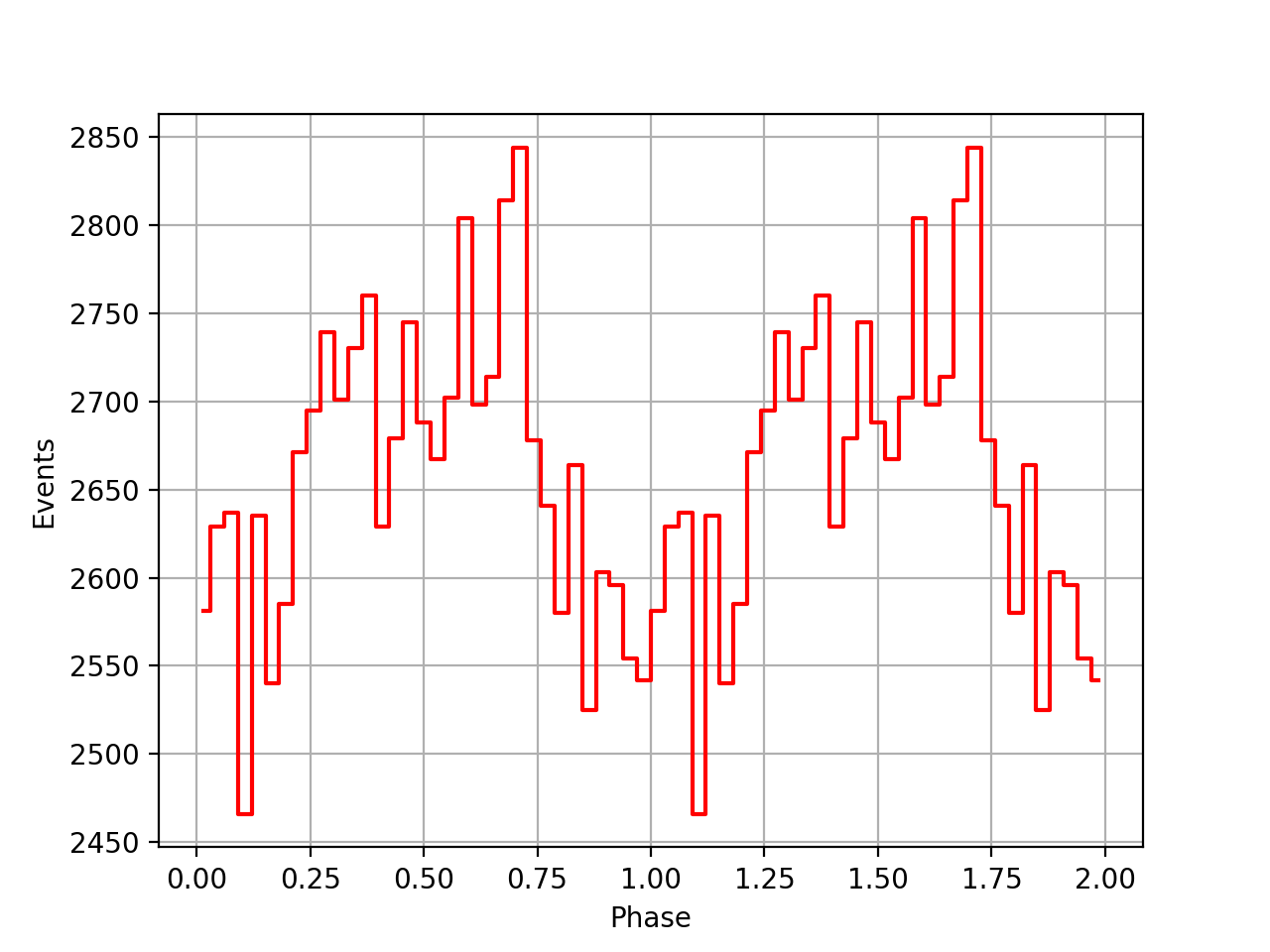
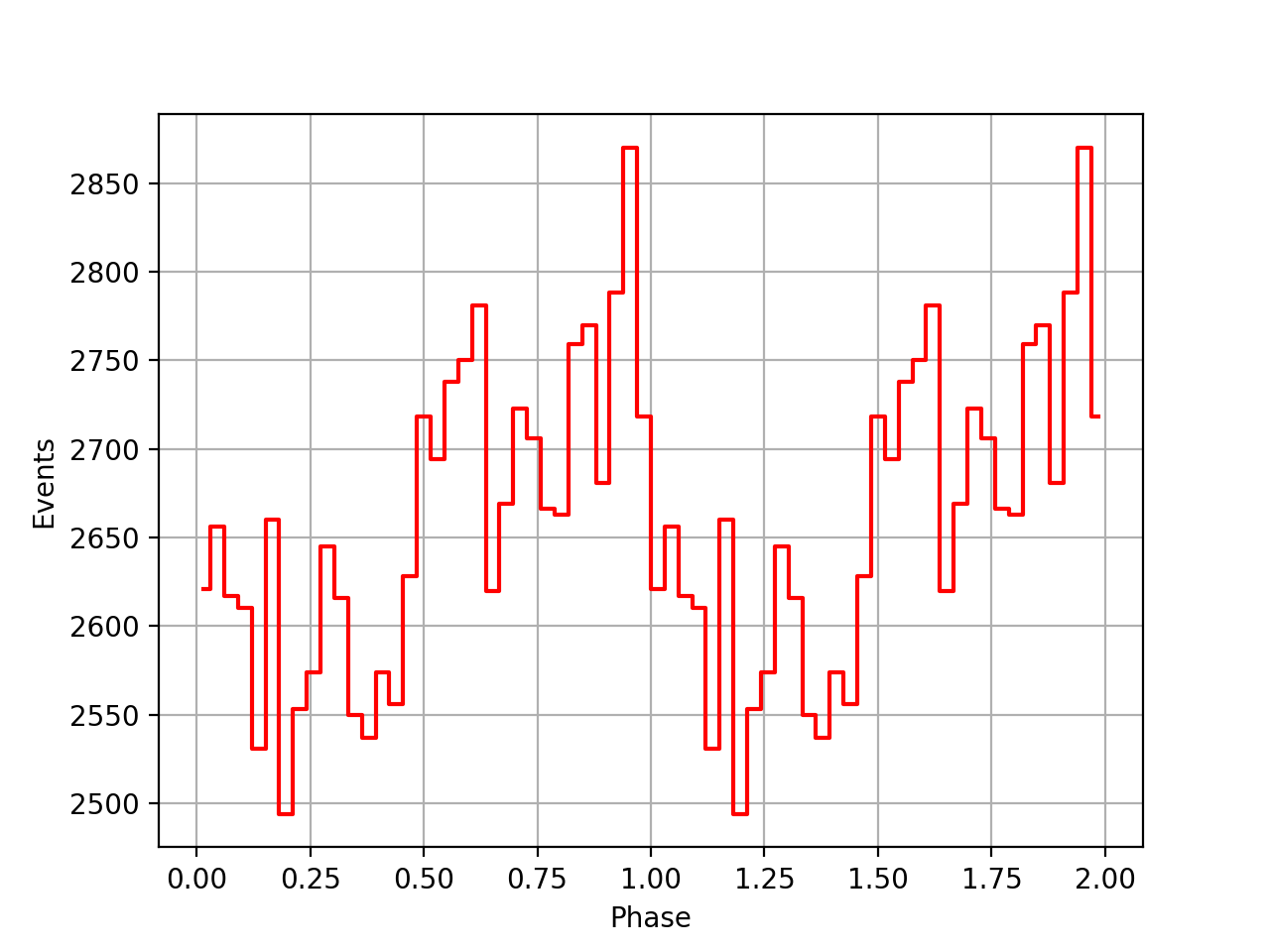
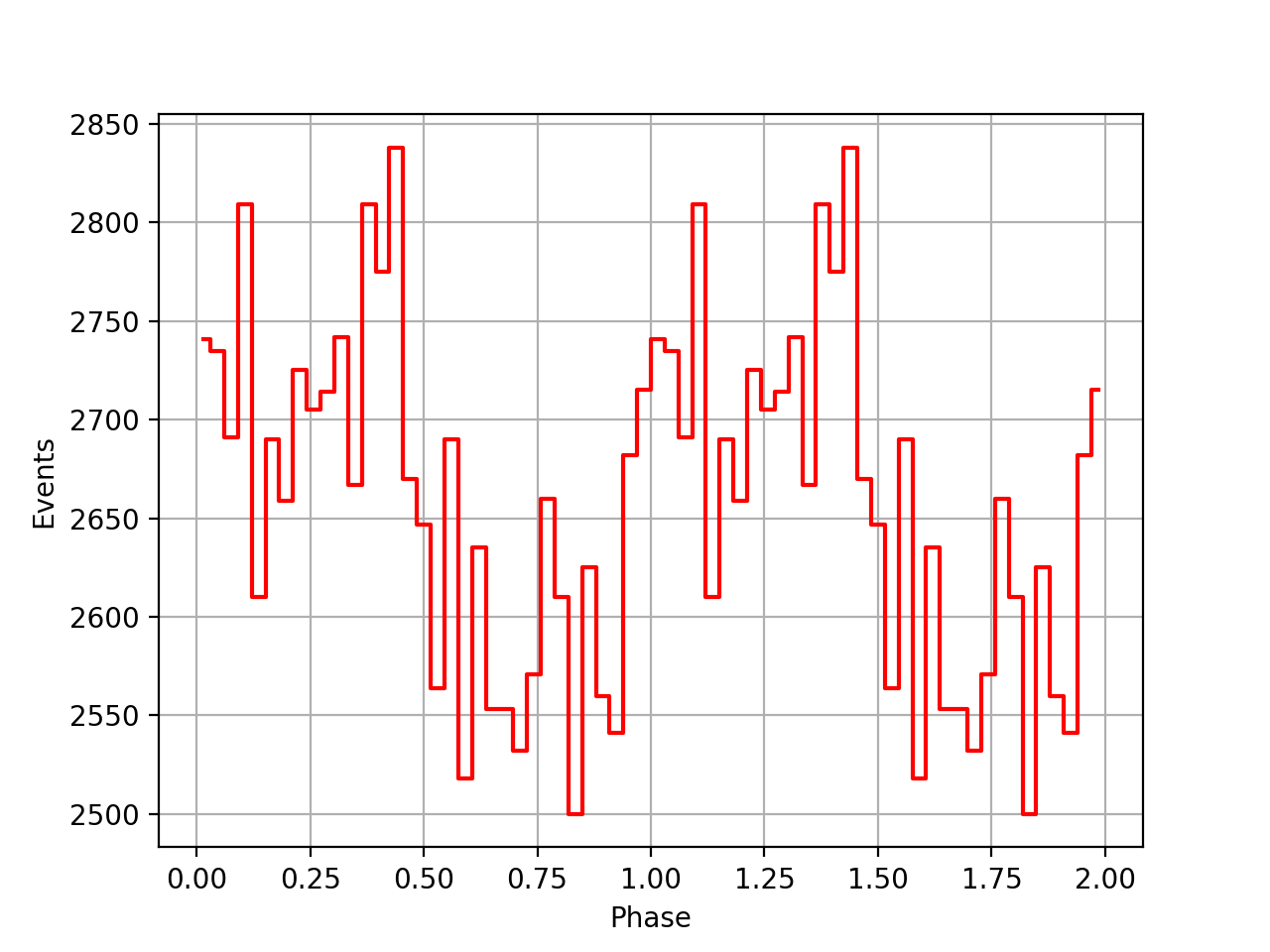
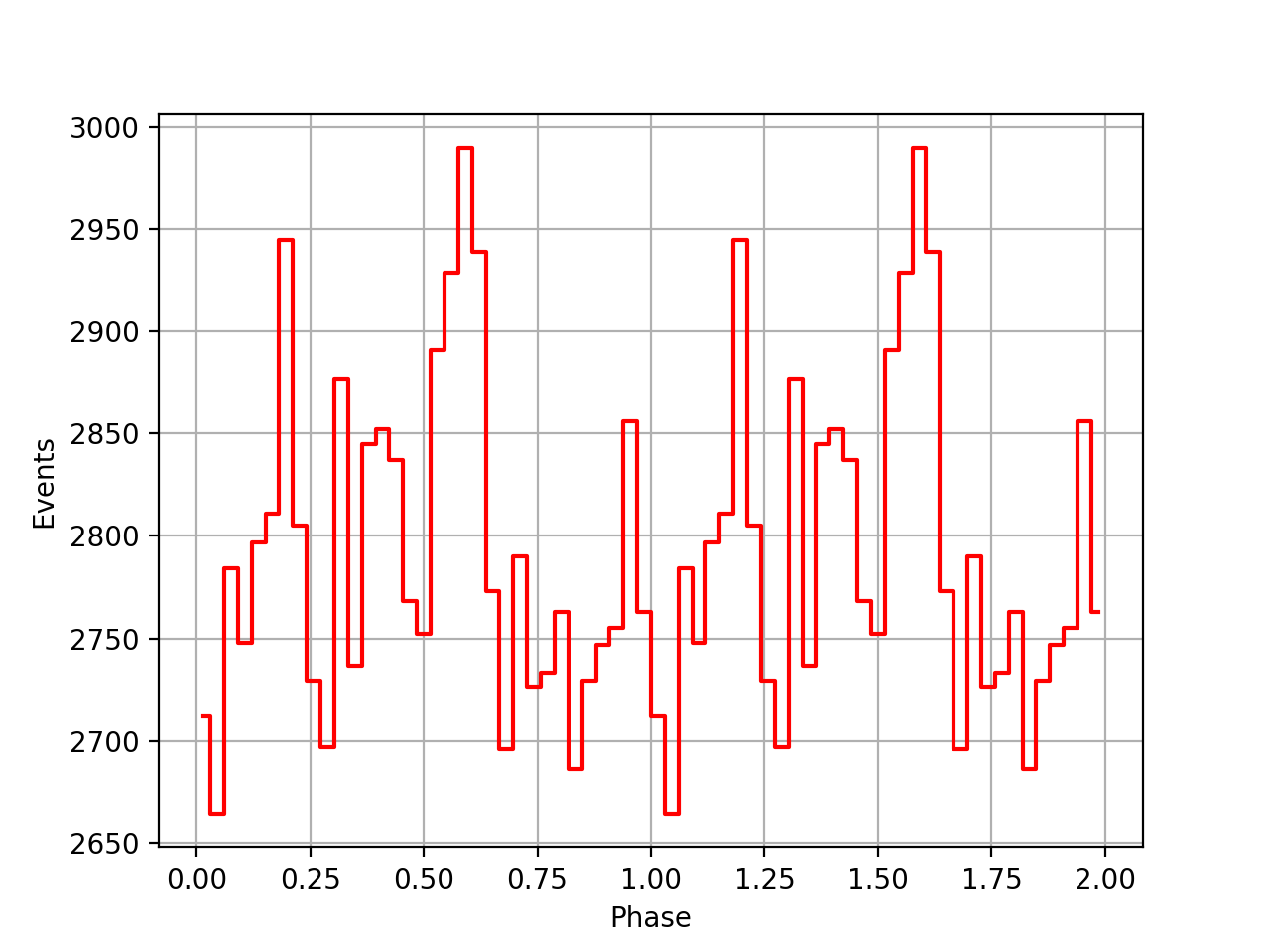
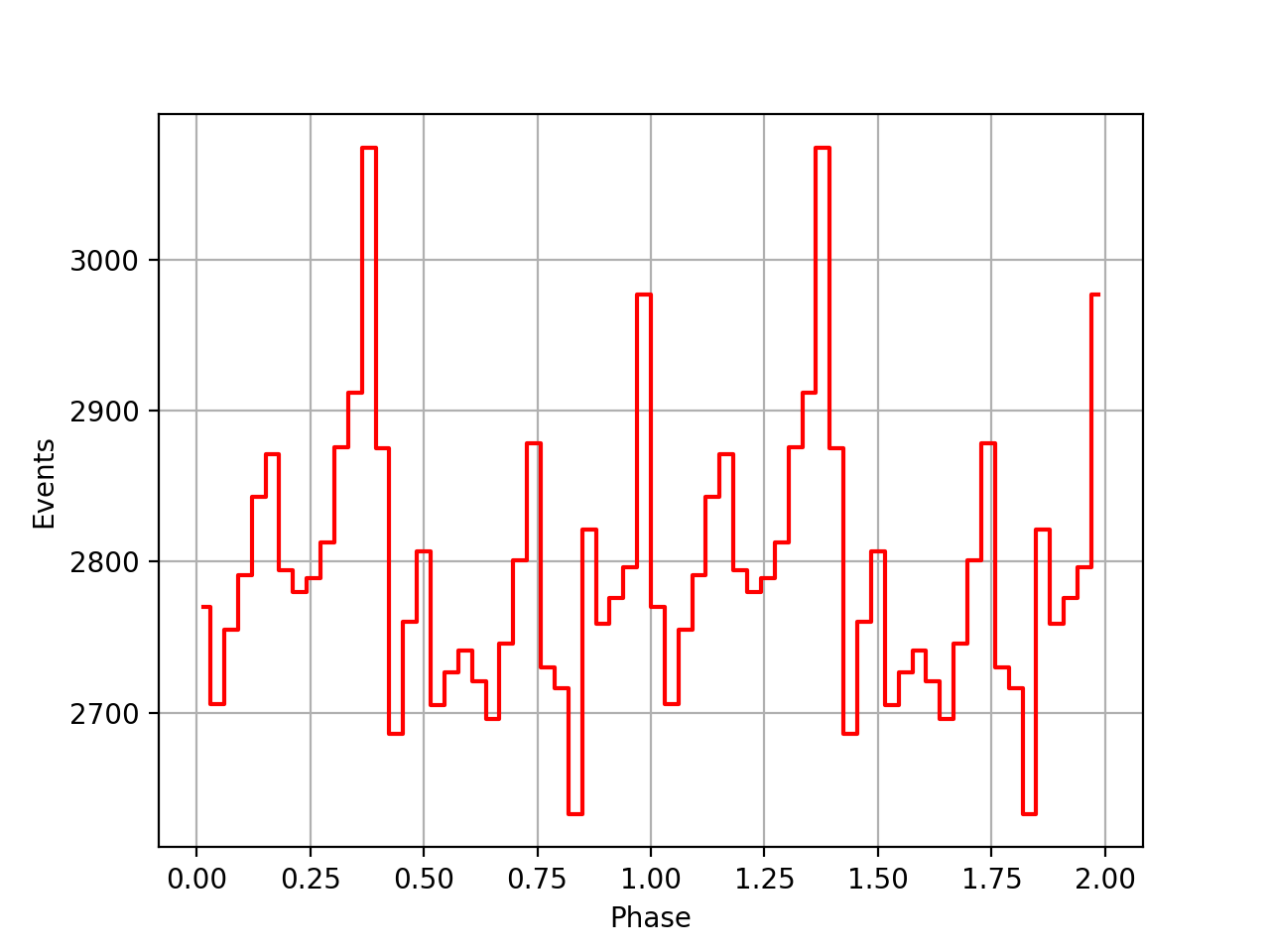
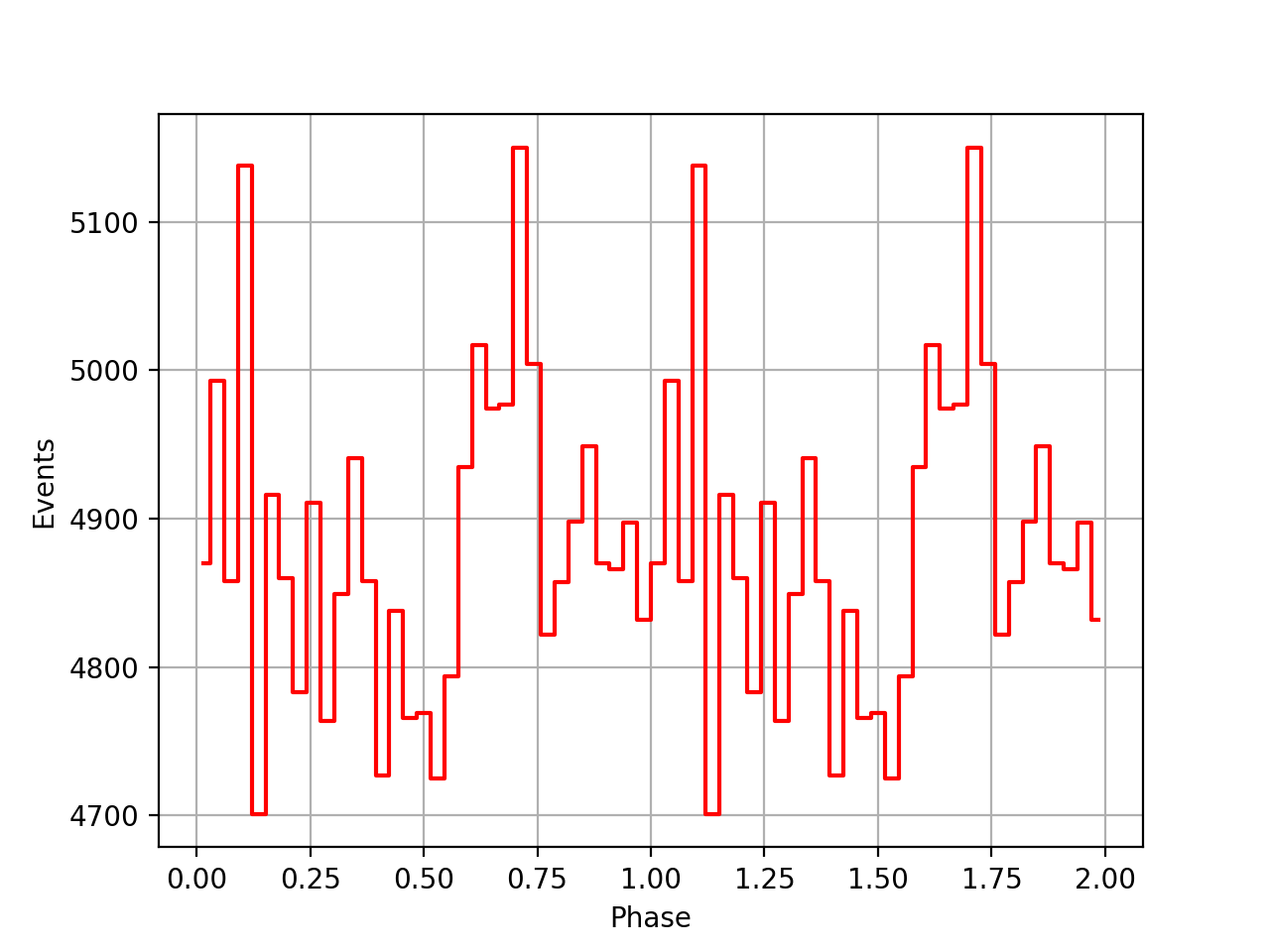
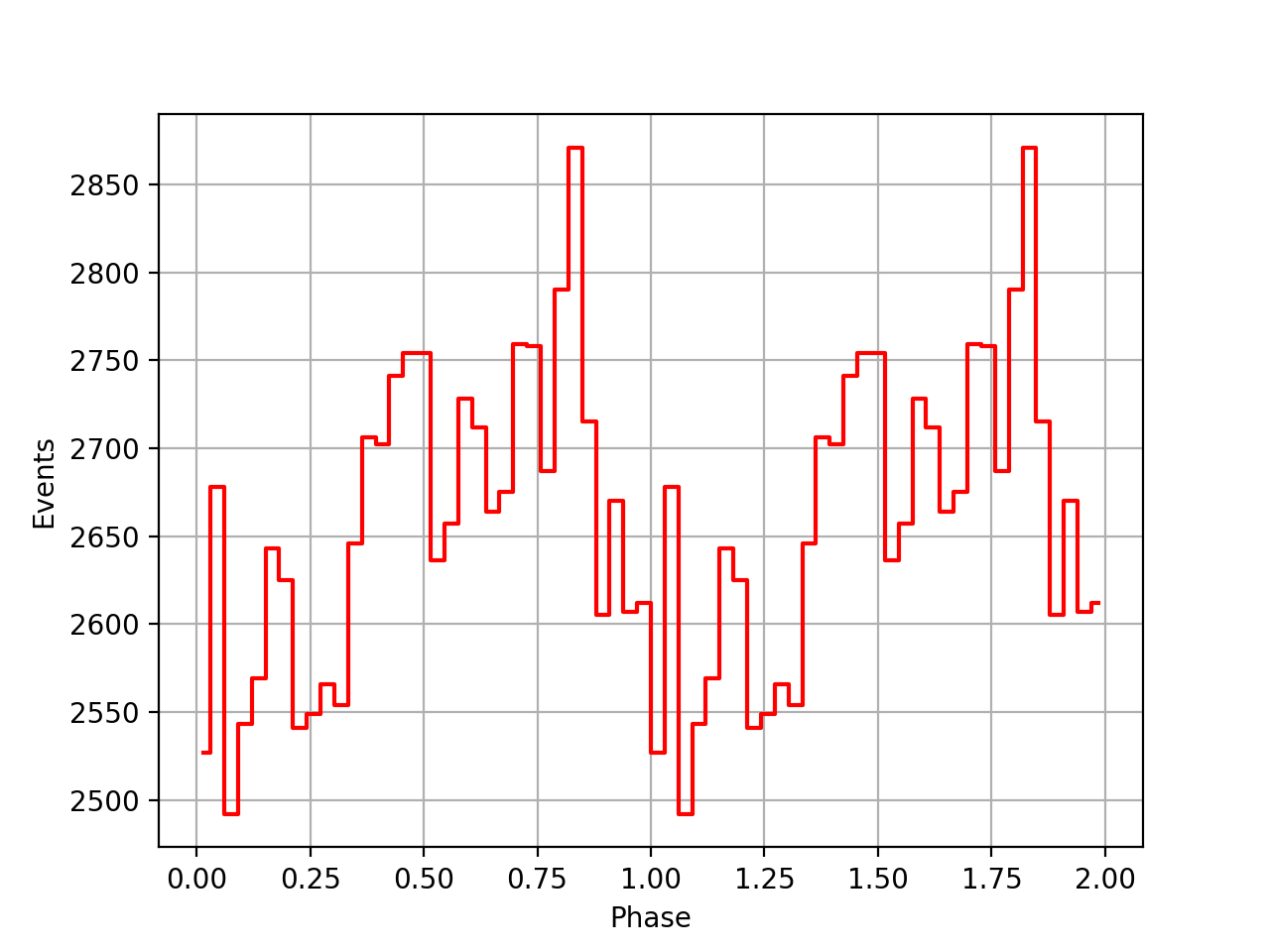
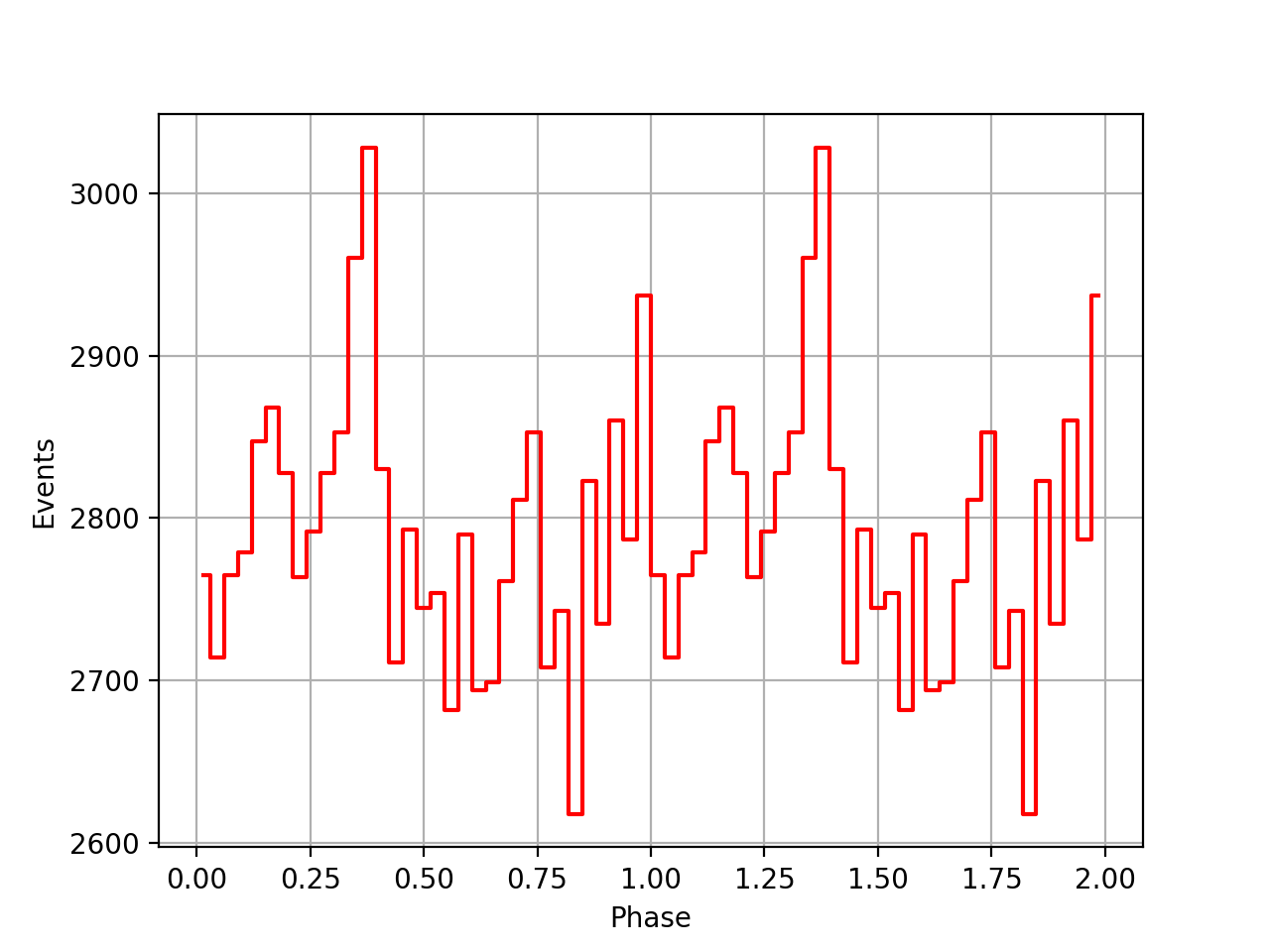
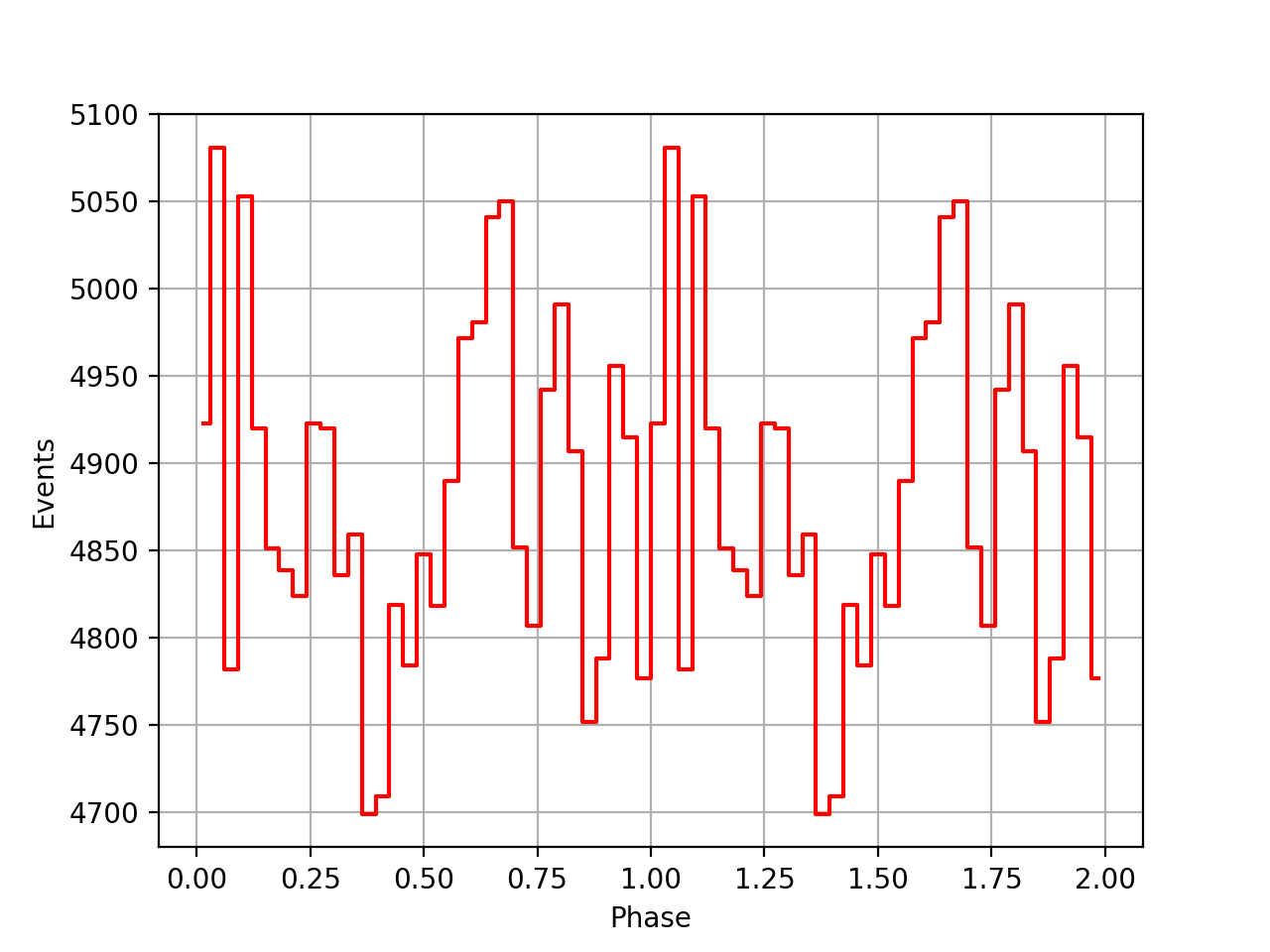
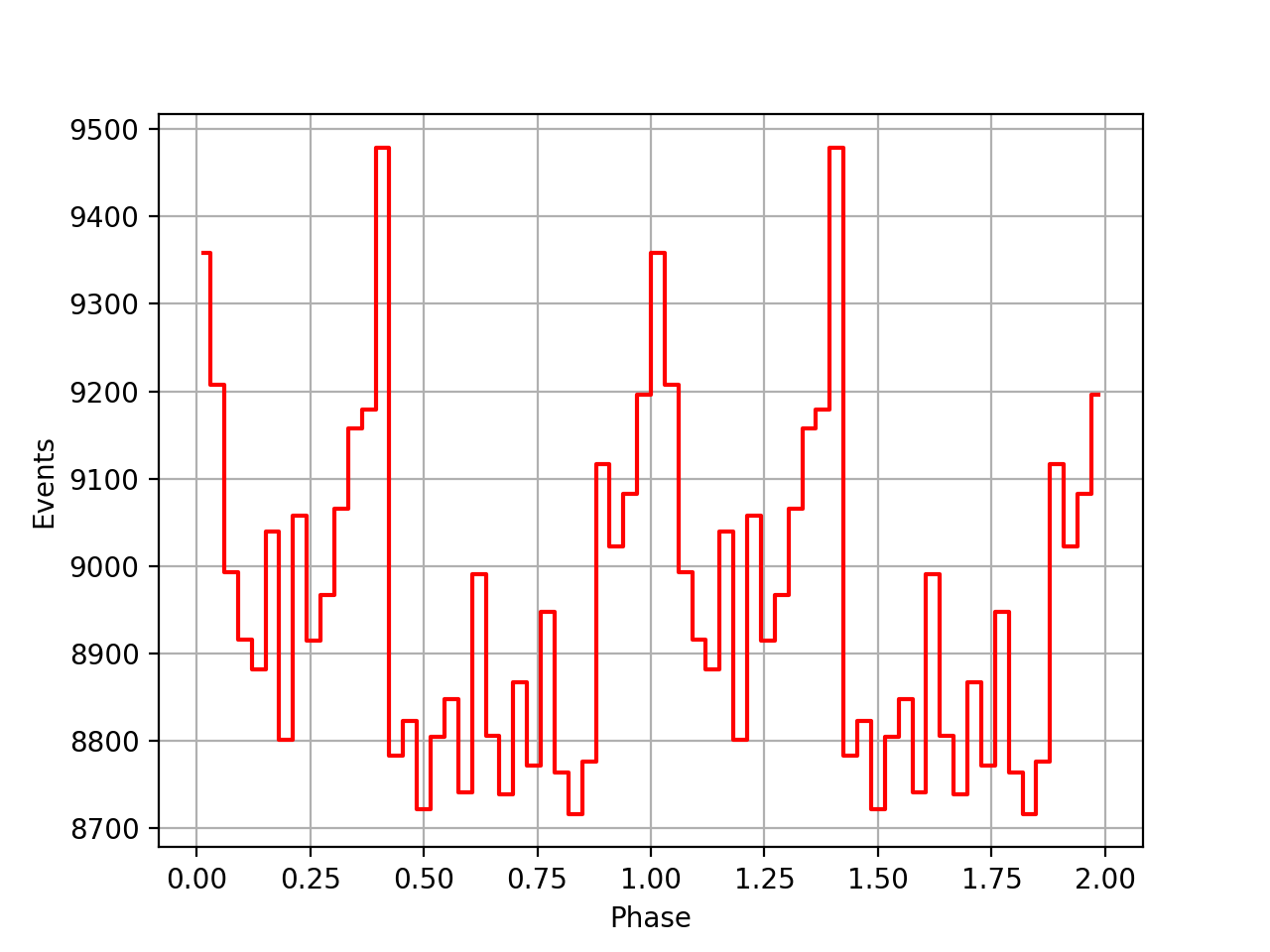
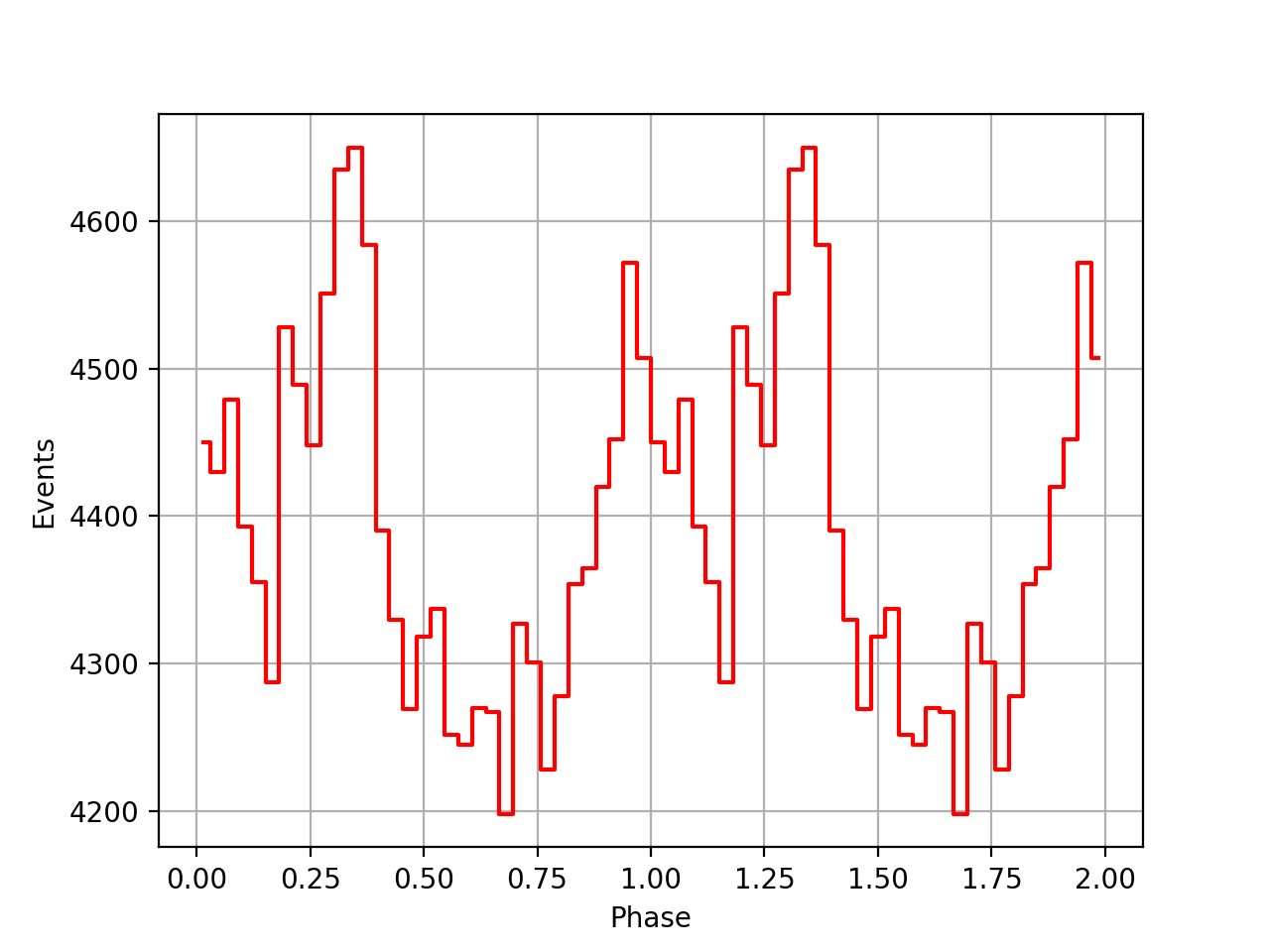
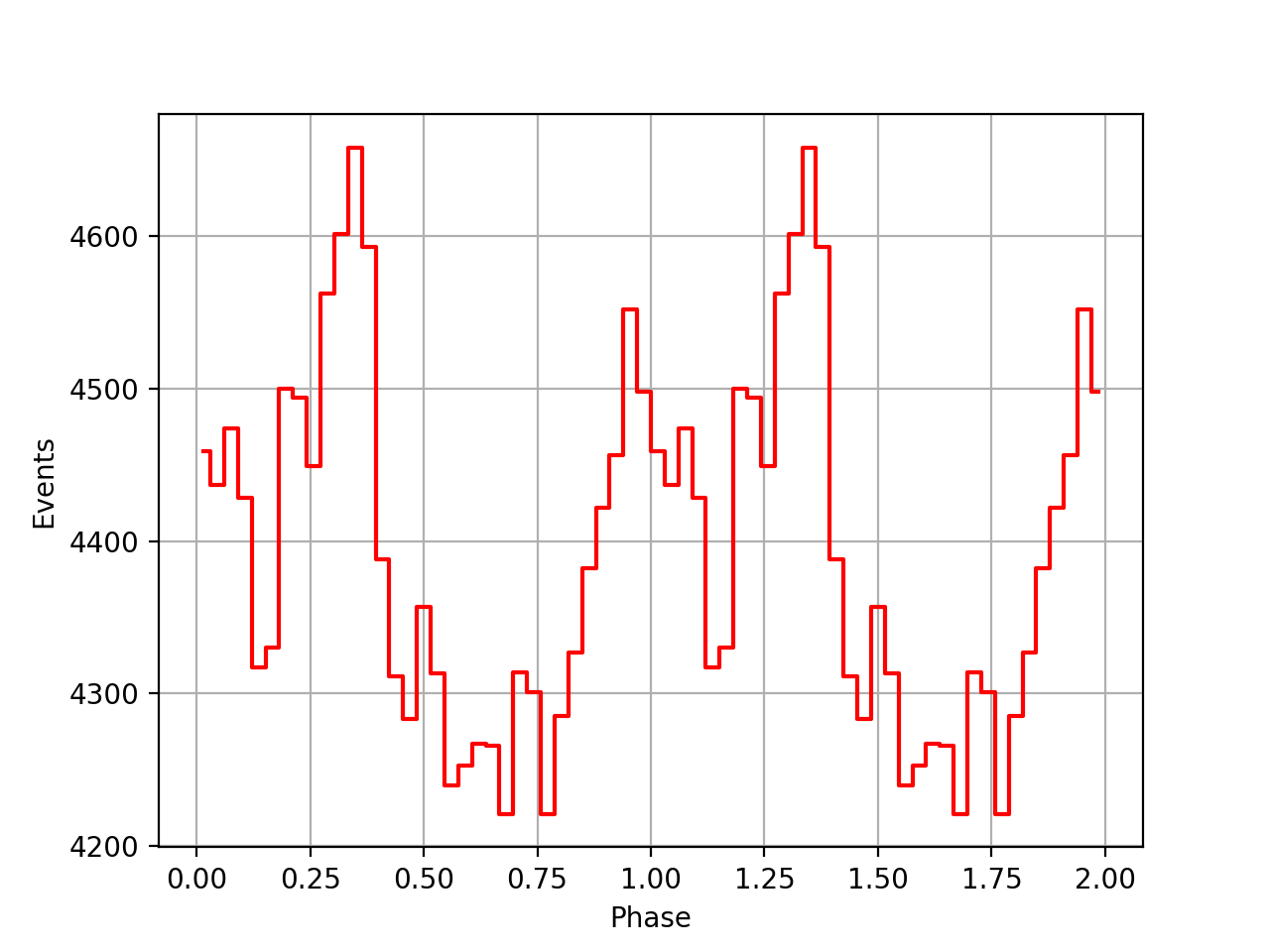
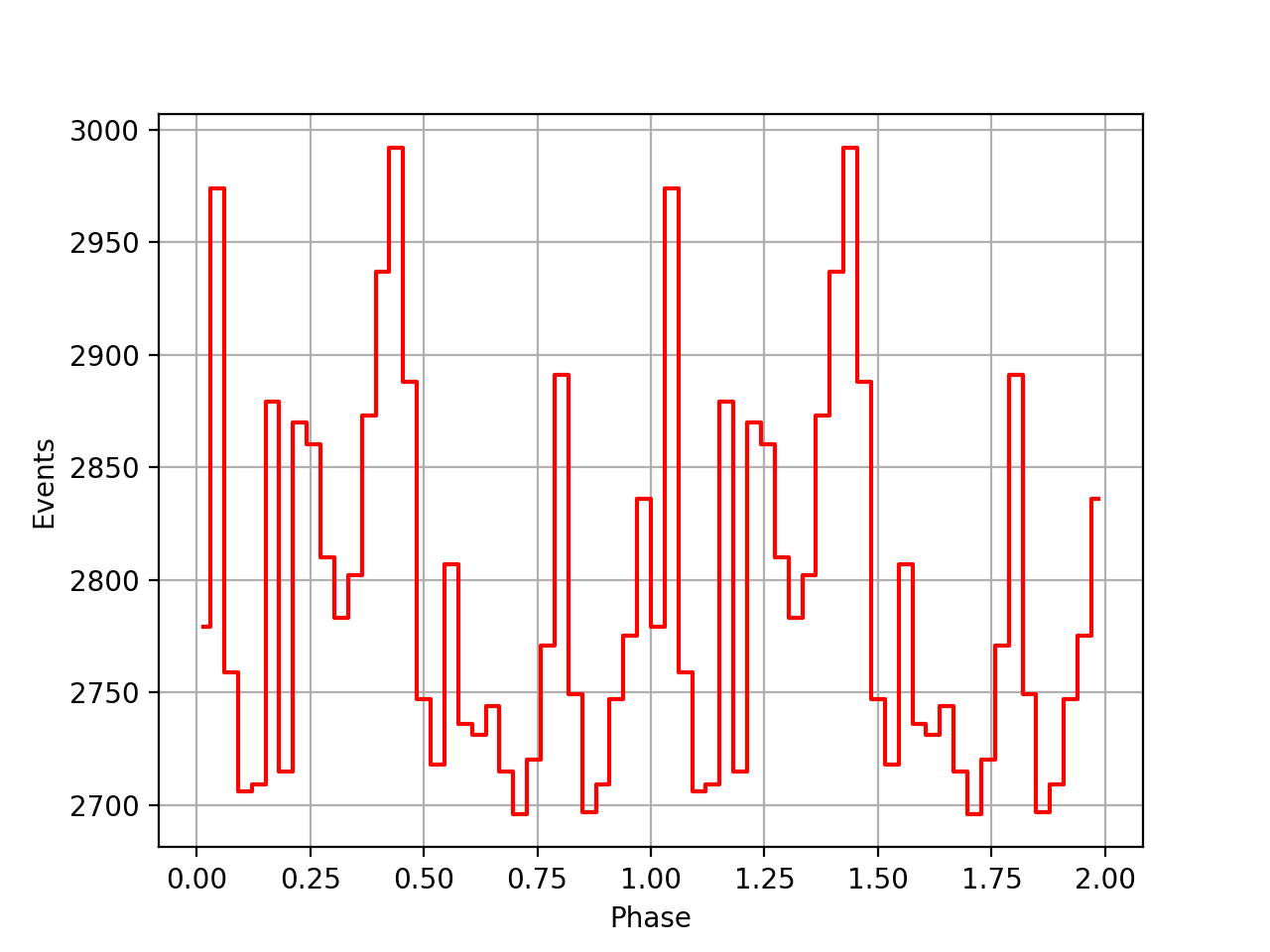
I also added a new comscript compulbin to generate a pulsar phase curve using an event ARM selection. Unfortunately I was not able to clearly detected the Crab pulsations with that script. The images below show two phasecurves (1-10 MeV, arm=±3), the left obtained for VP0001 and the right obtained for the combination of five VPs (0001, 0031, 0039, 0213, 0221). While in the left plot a possible pulsation is visible, nothing can be seen in the right curve.
 |
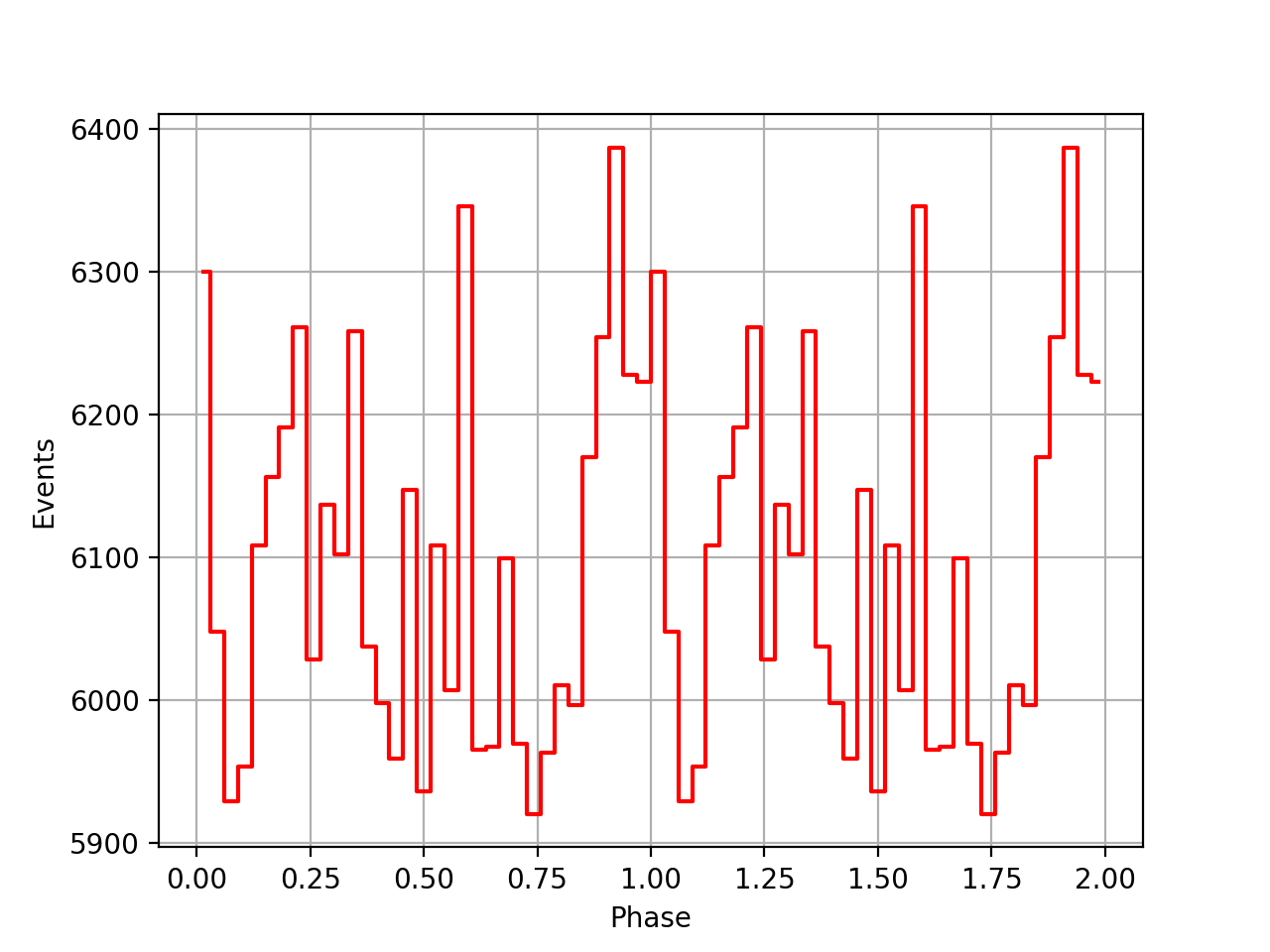 |
The question is now: why does the pulsar code not yet work? Maybe the code works but the ephemerides data are not interpreted correctly. Specifically, I use t0geo as the reference time for phase zero, yet this time refers to the geocentre and not the Solar System Barycentre. Werner sent me some COMPASS code, and from the code and some documents (see below) it appears that a conversion to the Solar System Barycentre is needed to correctly exploit the data. It’s a pitty that this correction is not added to the file which would avoid that things need to be computed.
#14
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
PULRGL- New task in which radio-phase zero is calculated at nominal epoch of pulsar ephemeris from Princeton catalogue. See COM-RP-ROL-DRG-65 for a description of the applied algorithm (from SCN No: ROL-55, Date: 1994-11-22)
#15
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
- File com-rp-rol-drg-065.pdf added
I found the report that is mentioned: com-rp-rol-drg-065.pdf.
There is a note that t0geo in the psrtime files should not be trusted. This quantity gives the infinite frequency geocentric UTC arrival time of a pulse, with the integer part of @t0
#16
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
- File com-rp-rol-drg-066.pdf added
Here is another document where the PULA20 code is described com-rp-rol-drg-066.pdf.
#17
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
- File ADA464615.pdf added
Here is an OSSE paper about pulsar timing, mentioning also the handling to t0geo: ADA464615.pdf.
#18
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
- File pulsar_vp0001.png added
#19
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
- File pulsar_vp0001_arm2.0.png added
- File pulsar_vp0001_arm2.5.png added
- File pulsar_vp0001_arm3.5.png added
- File pulsar_vp0001_arm4.0.png added
- File pulsar_vp0001_arm4.5.png added
- File pulsar_vp0001_arm5.0.png added
- File pulsar_vp0001_arm5.5.png added
- File pulsar_vp0001_arm6.0.png added
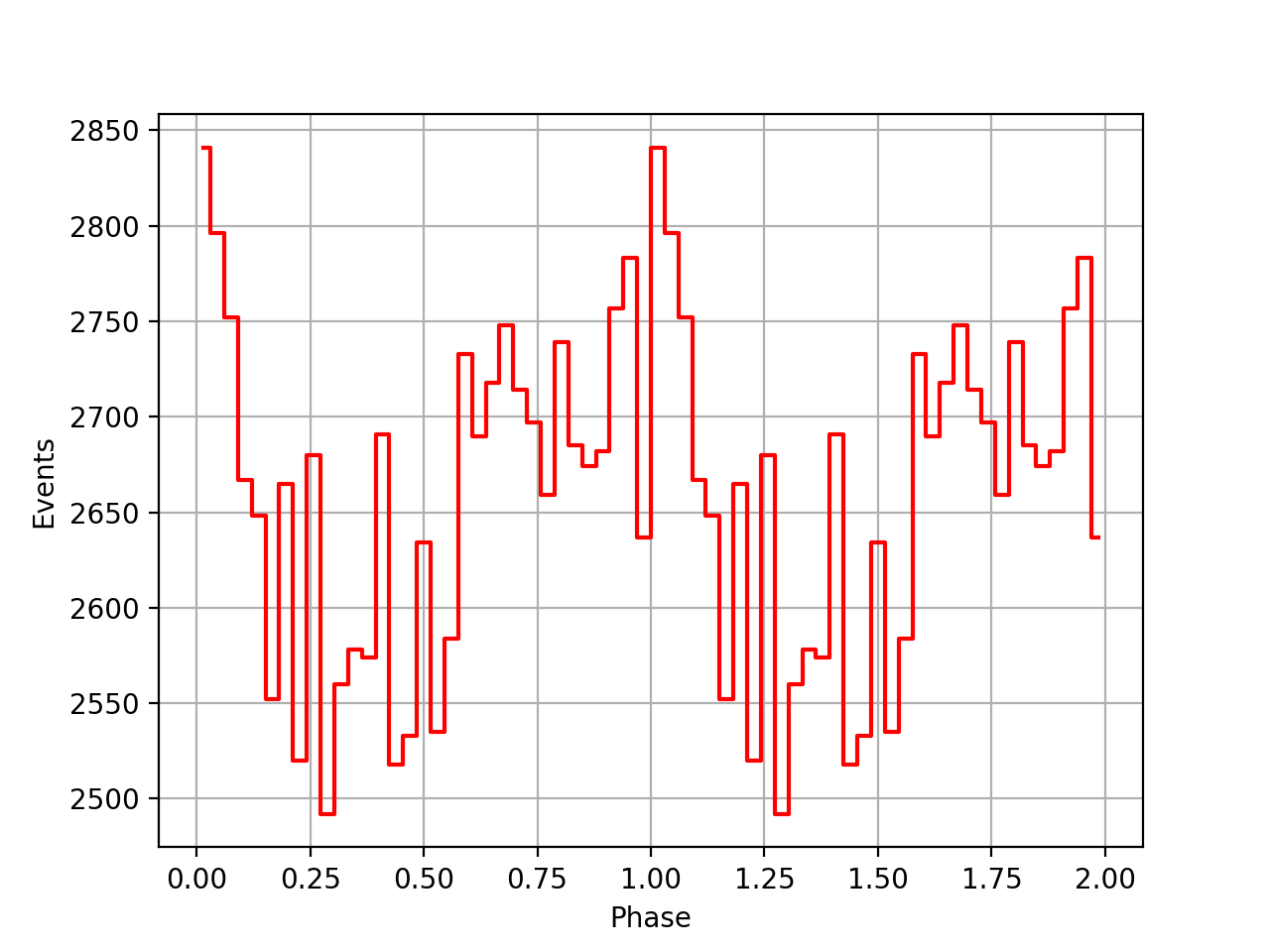
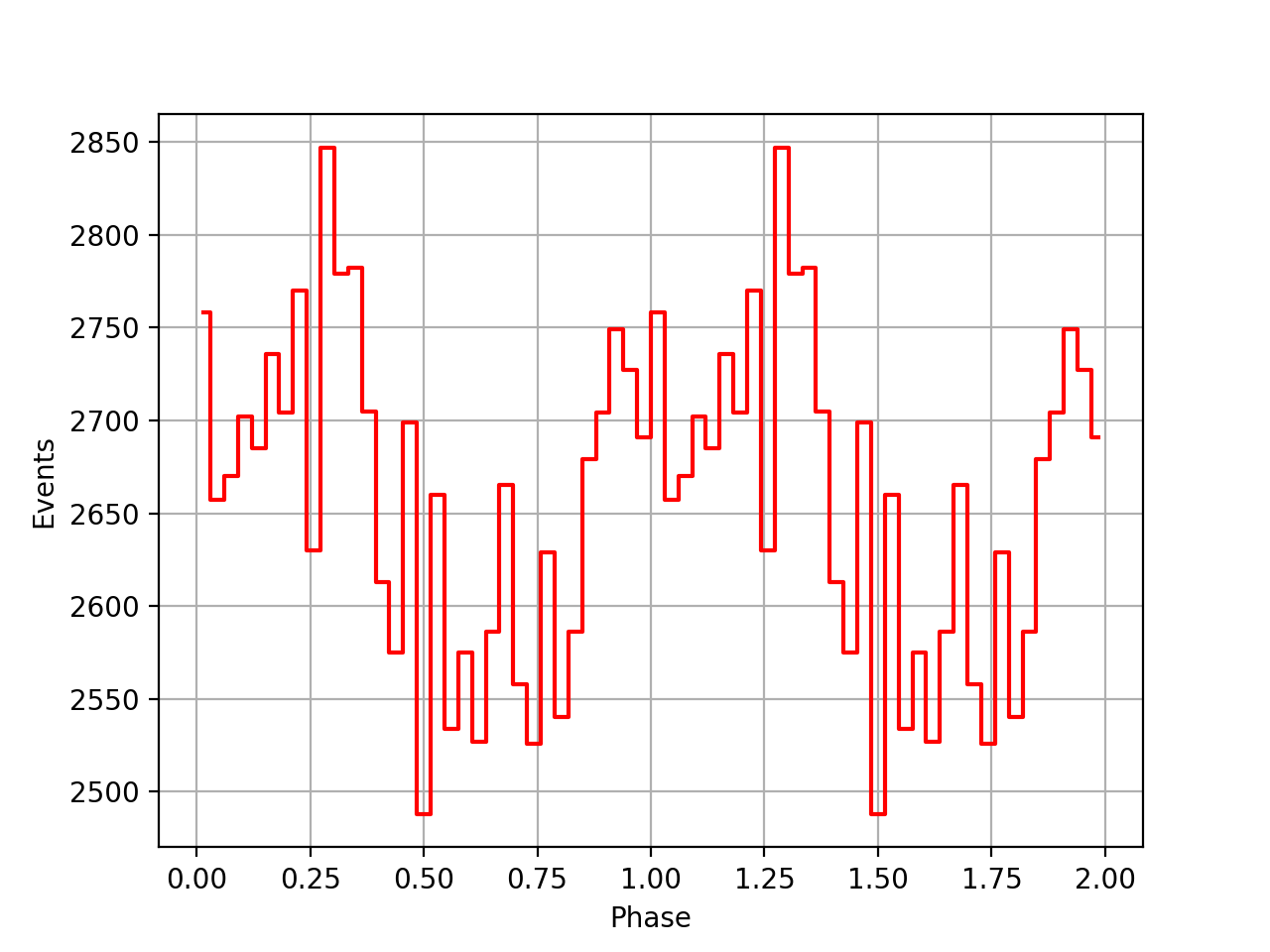
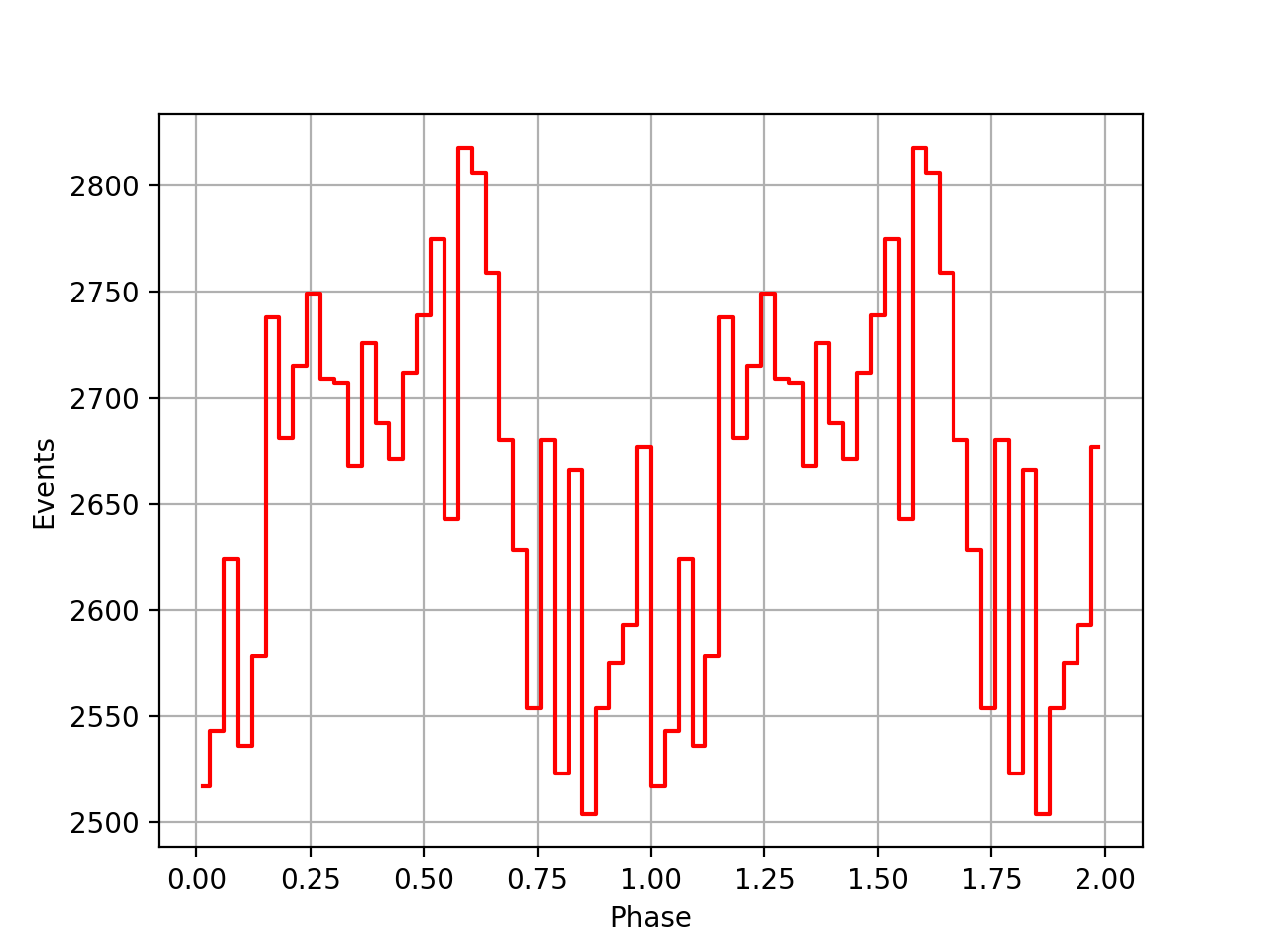
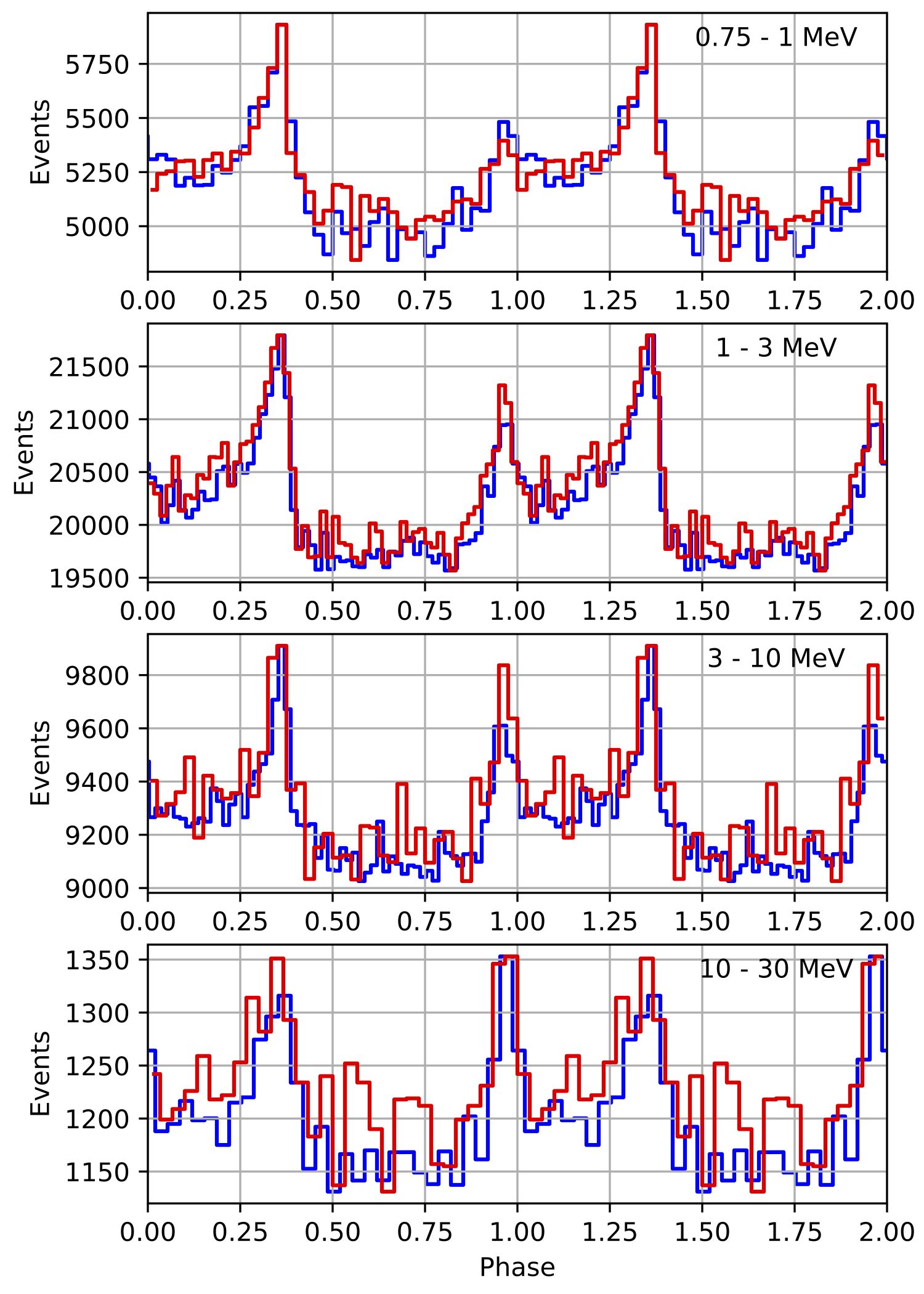
Going back to VP0001 probably shows that the timing code actually works, yet the issue is the interpretation of the t0geo which mixes things up once ephemerides are combined over a longer period.
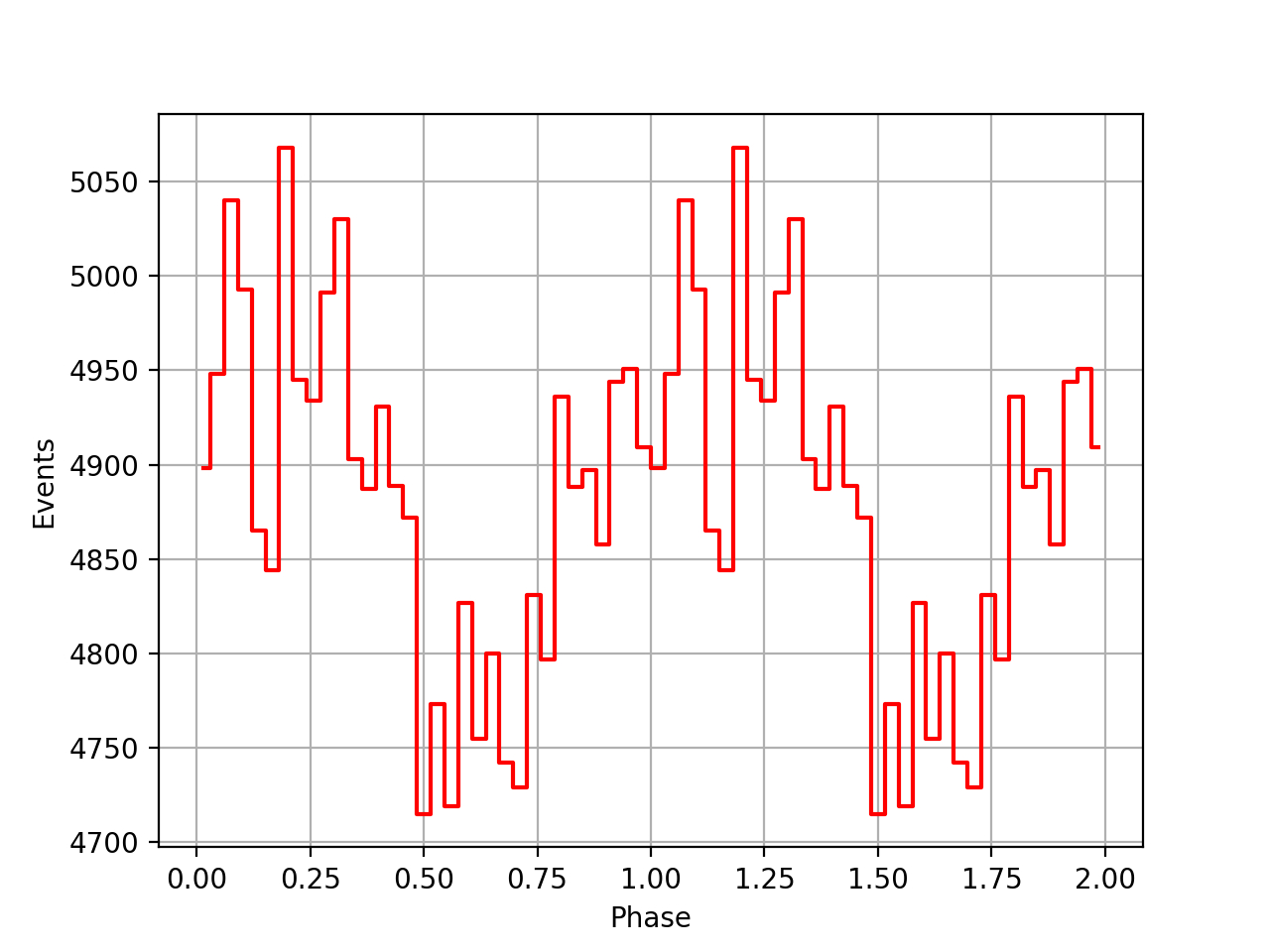
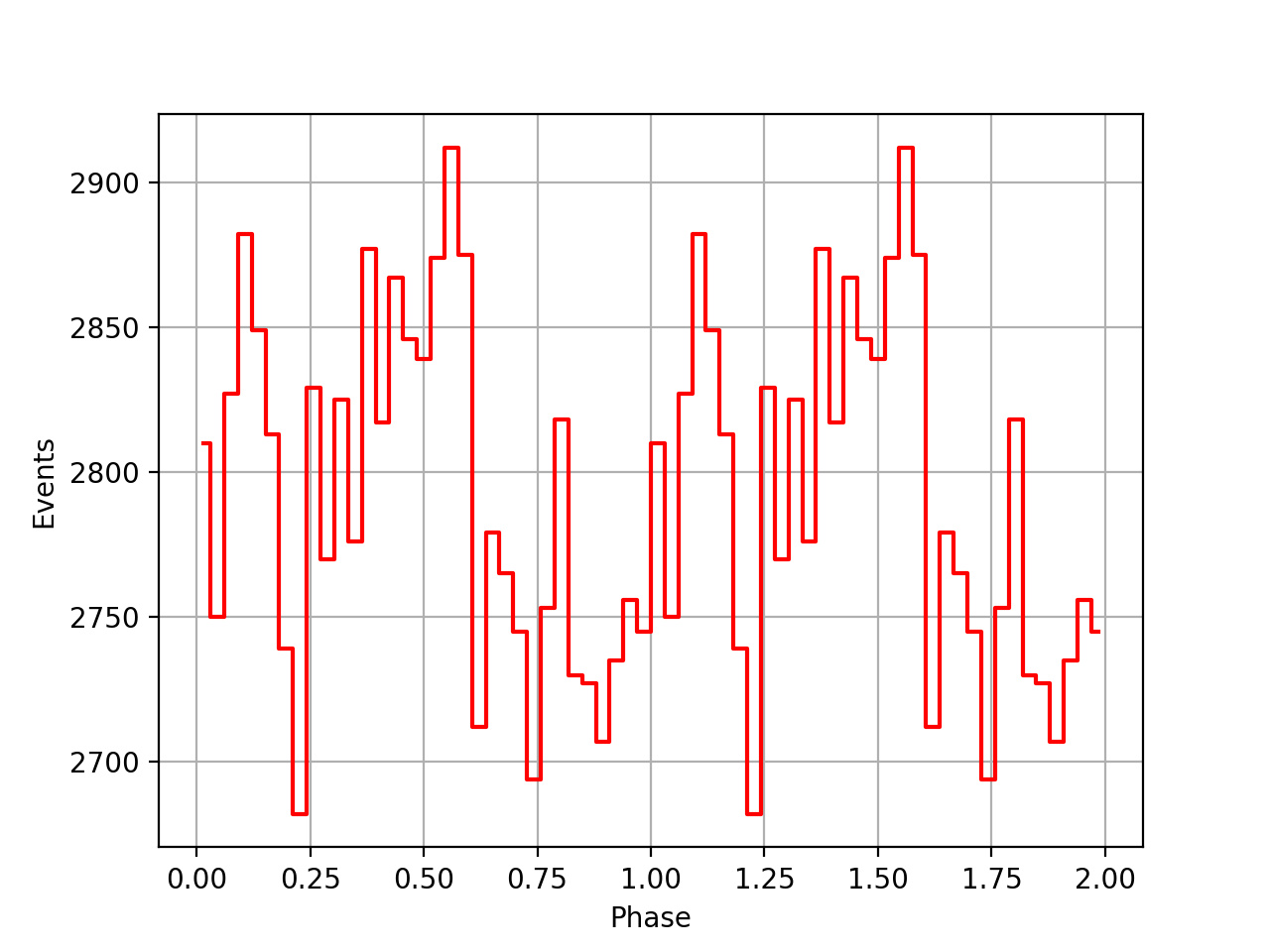
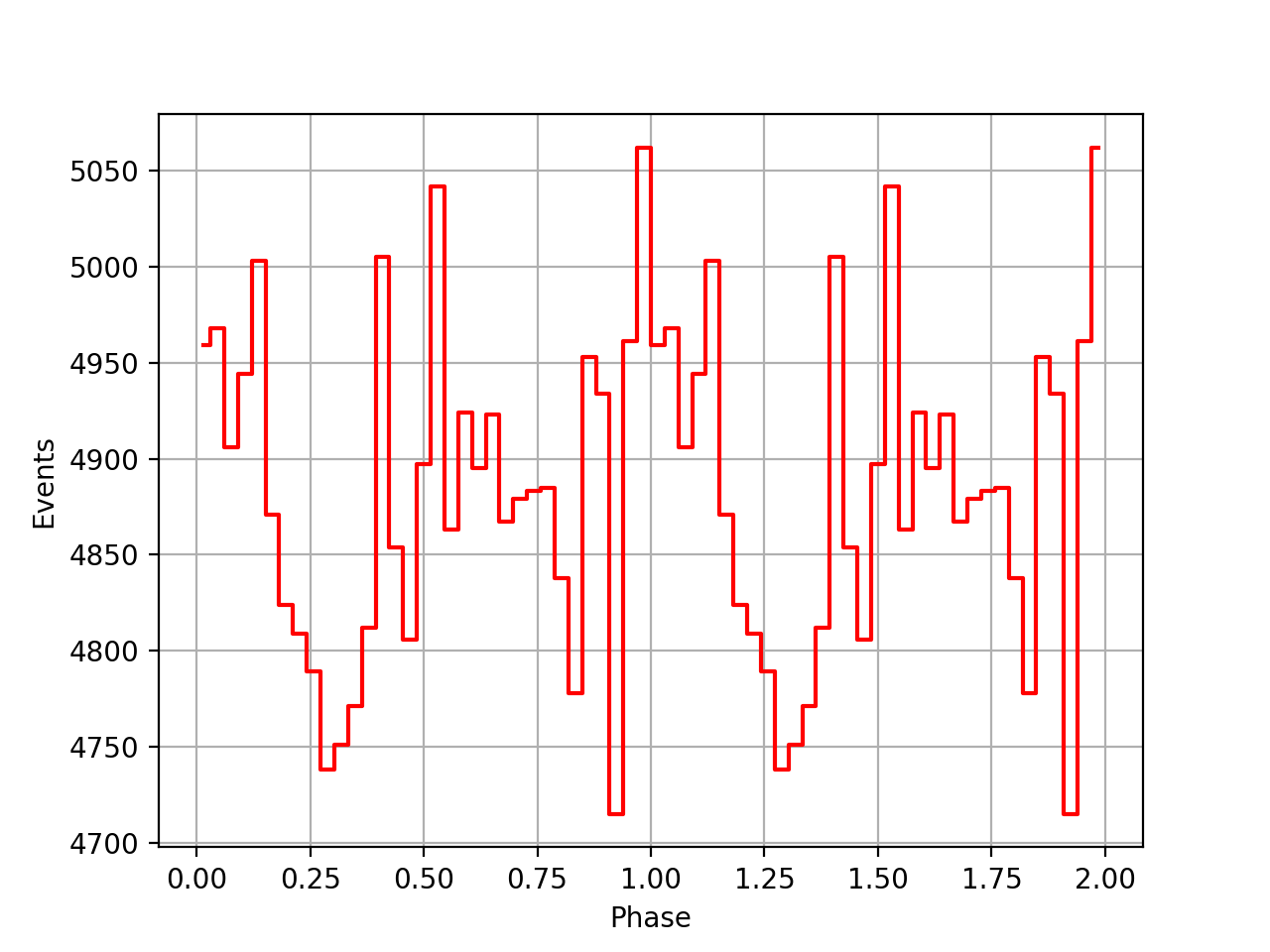
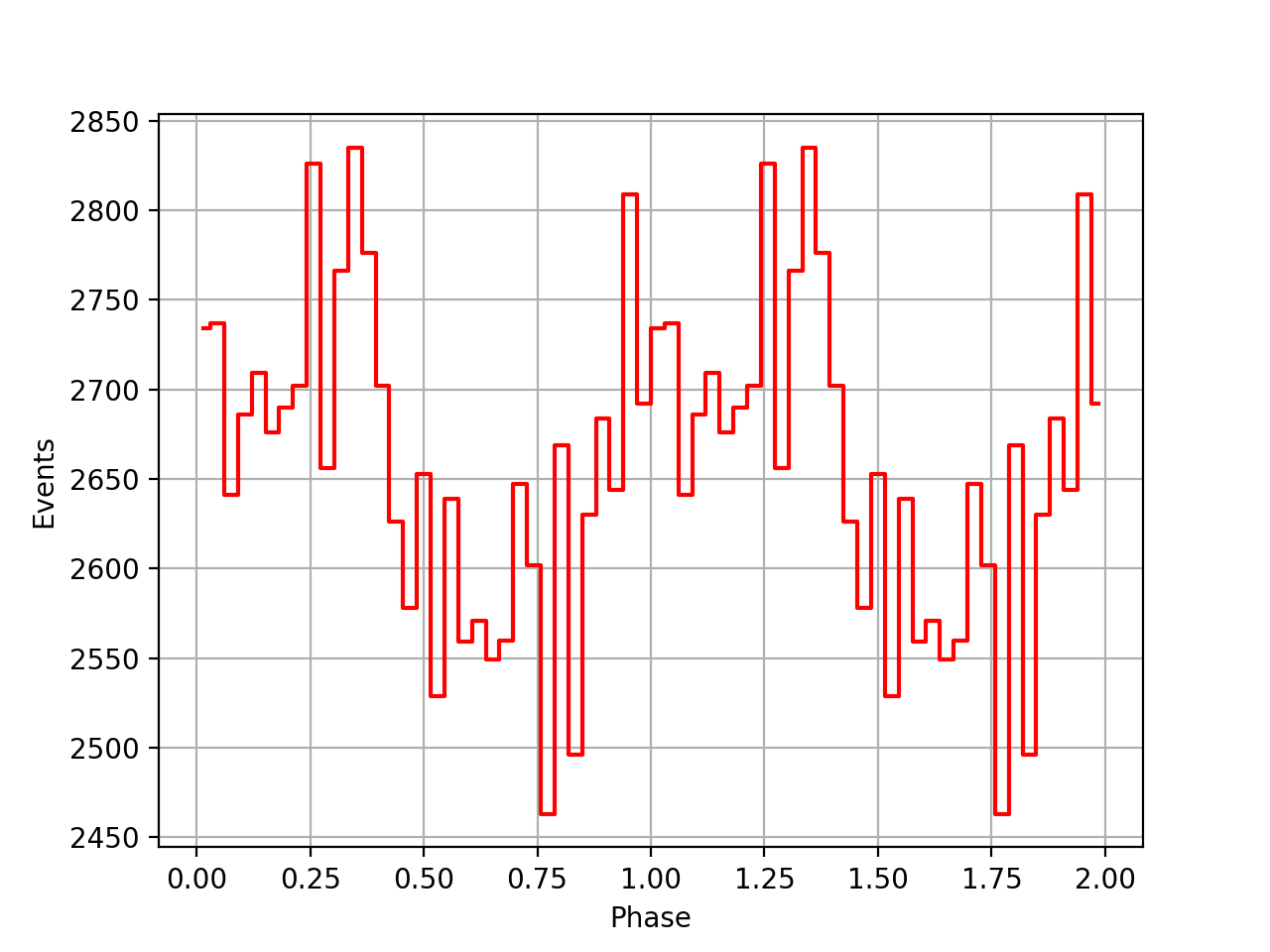
Below the VP0001 phasecurves for different ARM window sizes. An ARM window of ±3.5 seems to give a maximum modulation, and this value was actually used in at least some COMPTEL studies. For a smaller or larger ARM window the modulation becomes weaker, as expected.
±2  |
±2.5 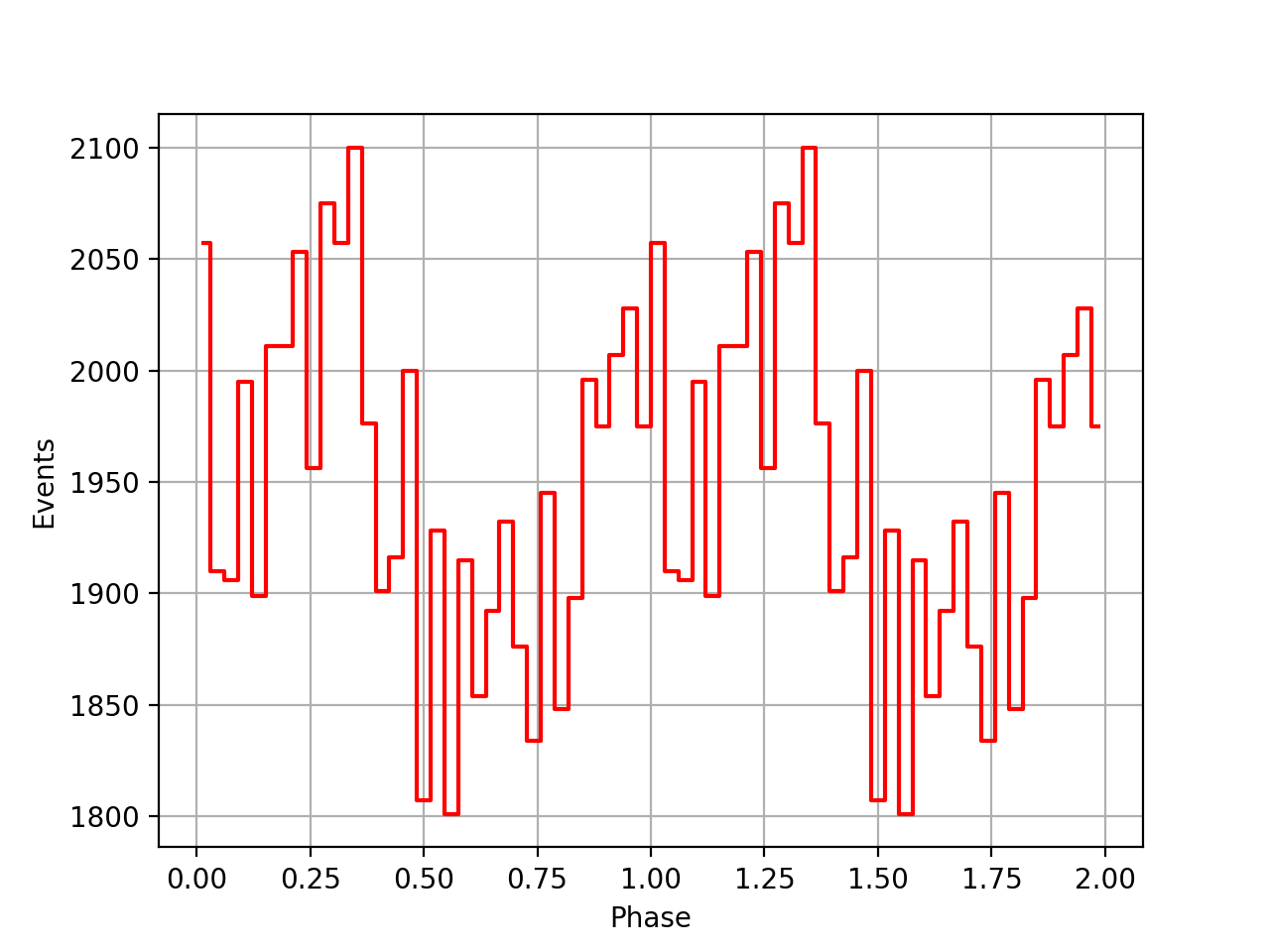 |
±3  |
±3.5 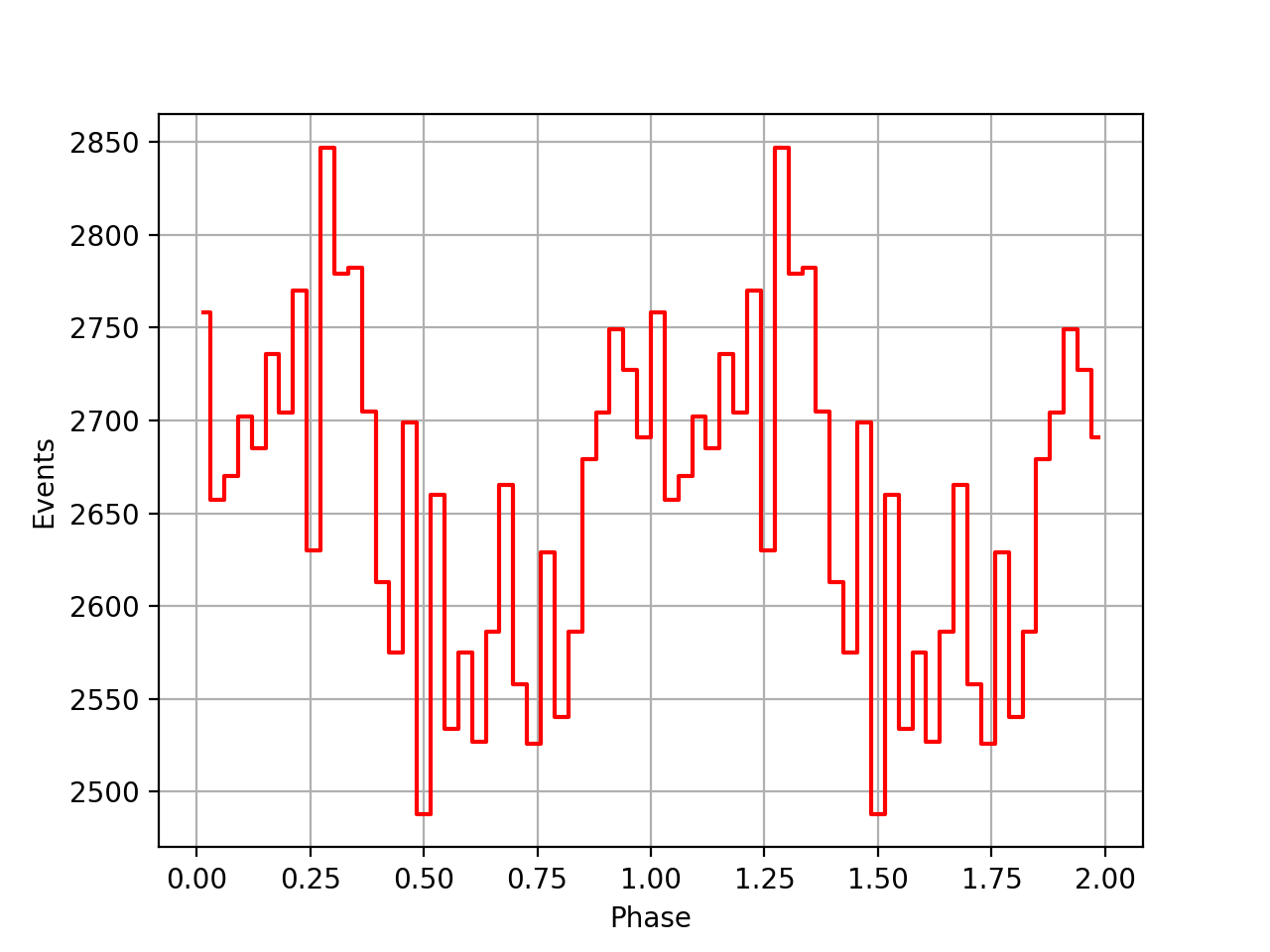 |
±4 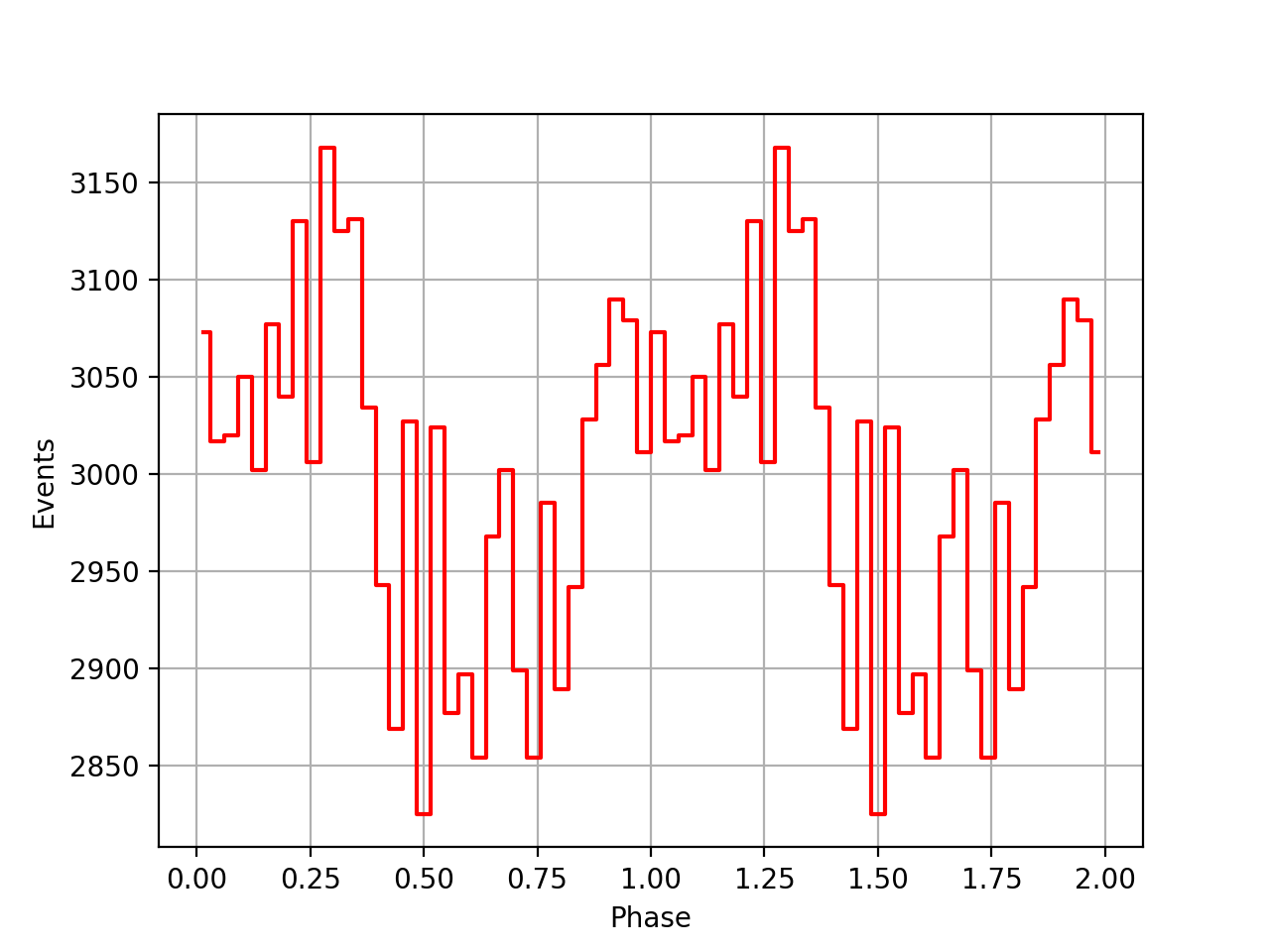 |
±4.5 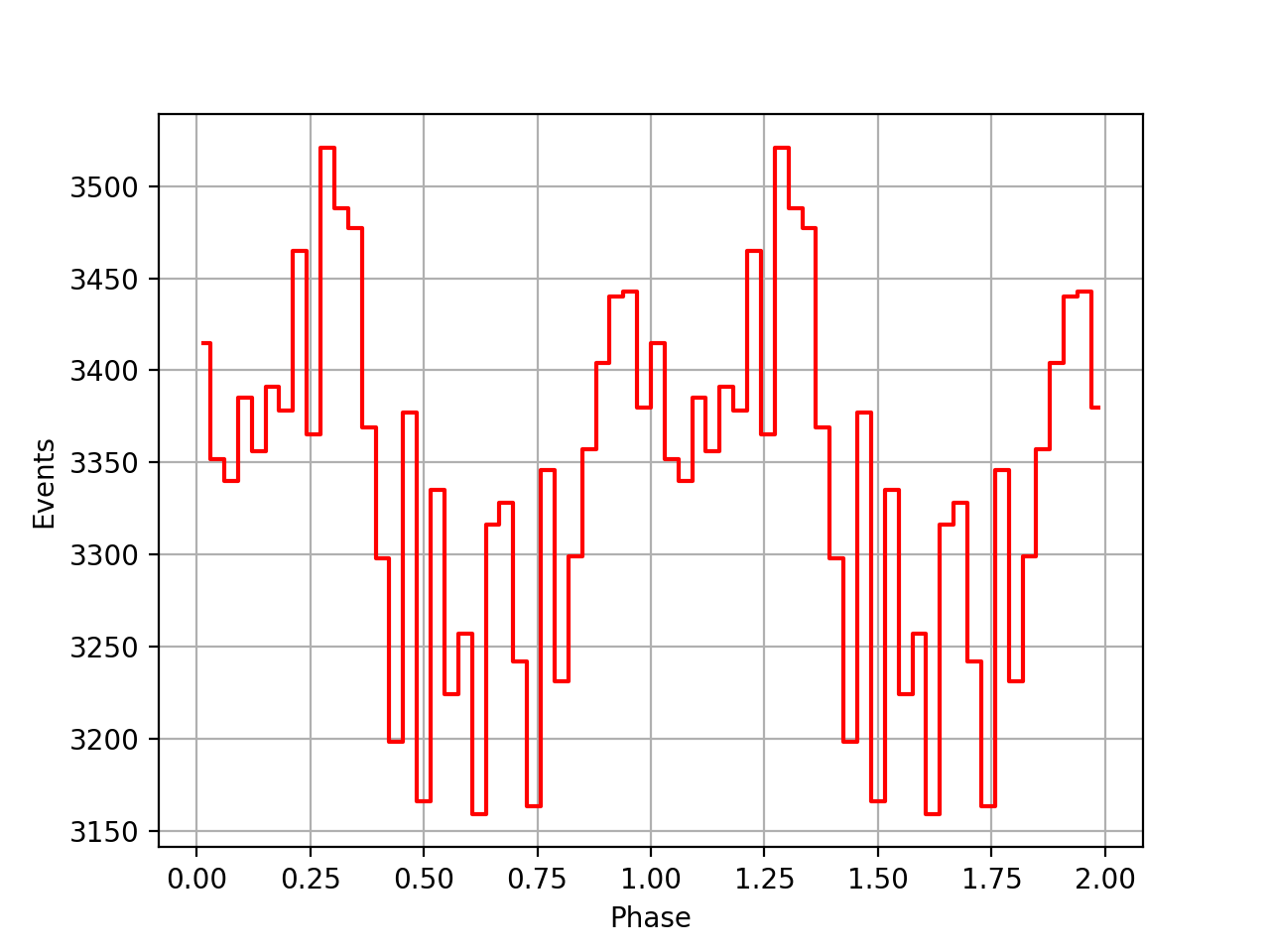 |
±5 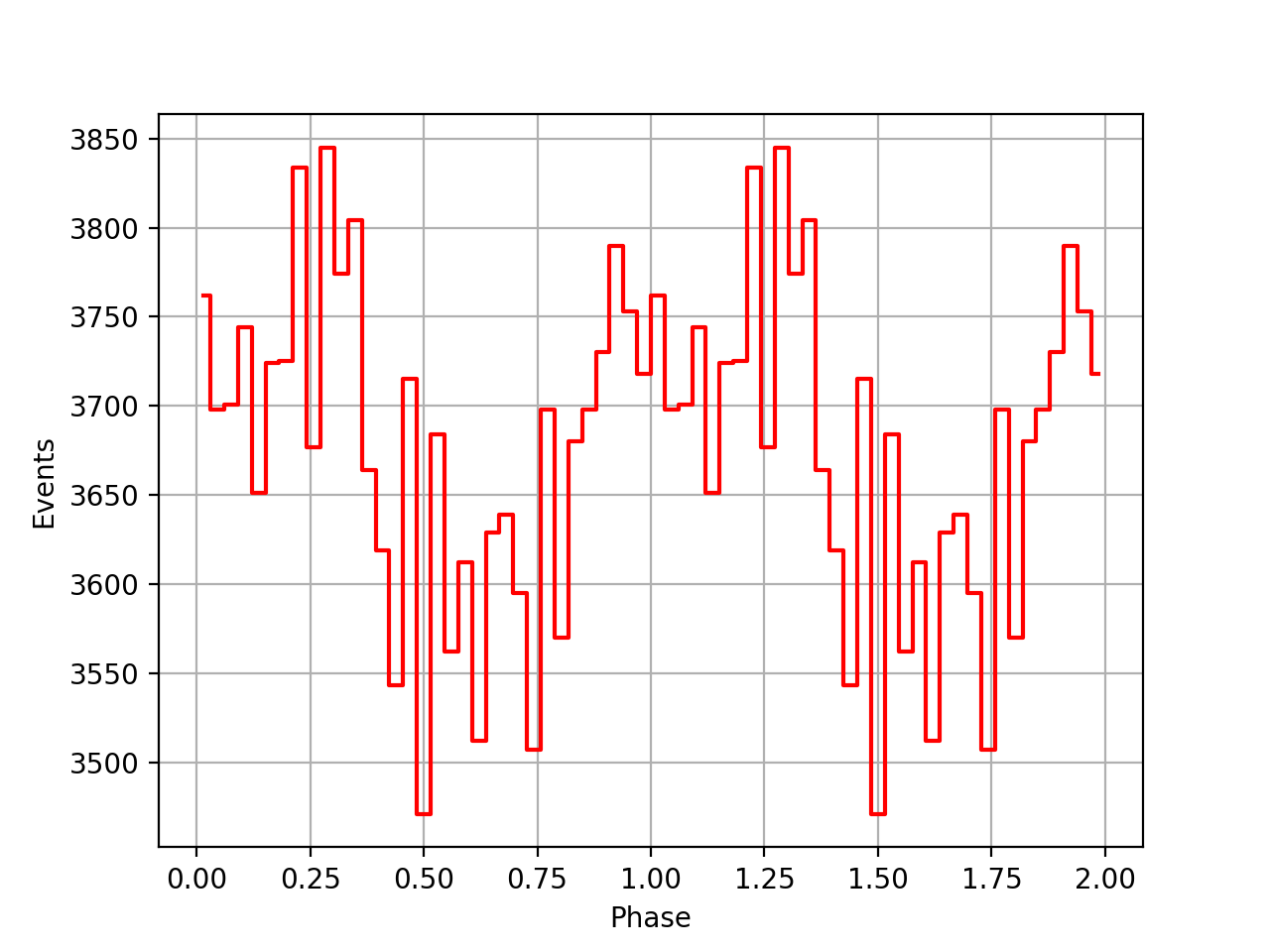 |
±5.5 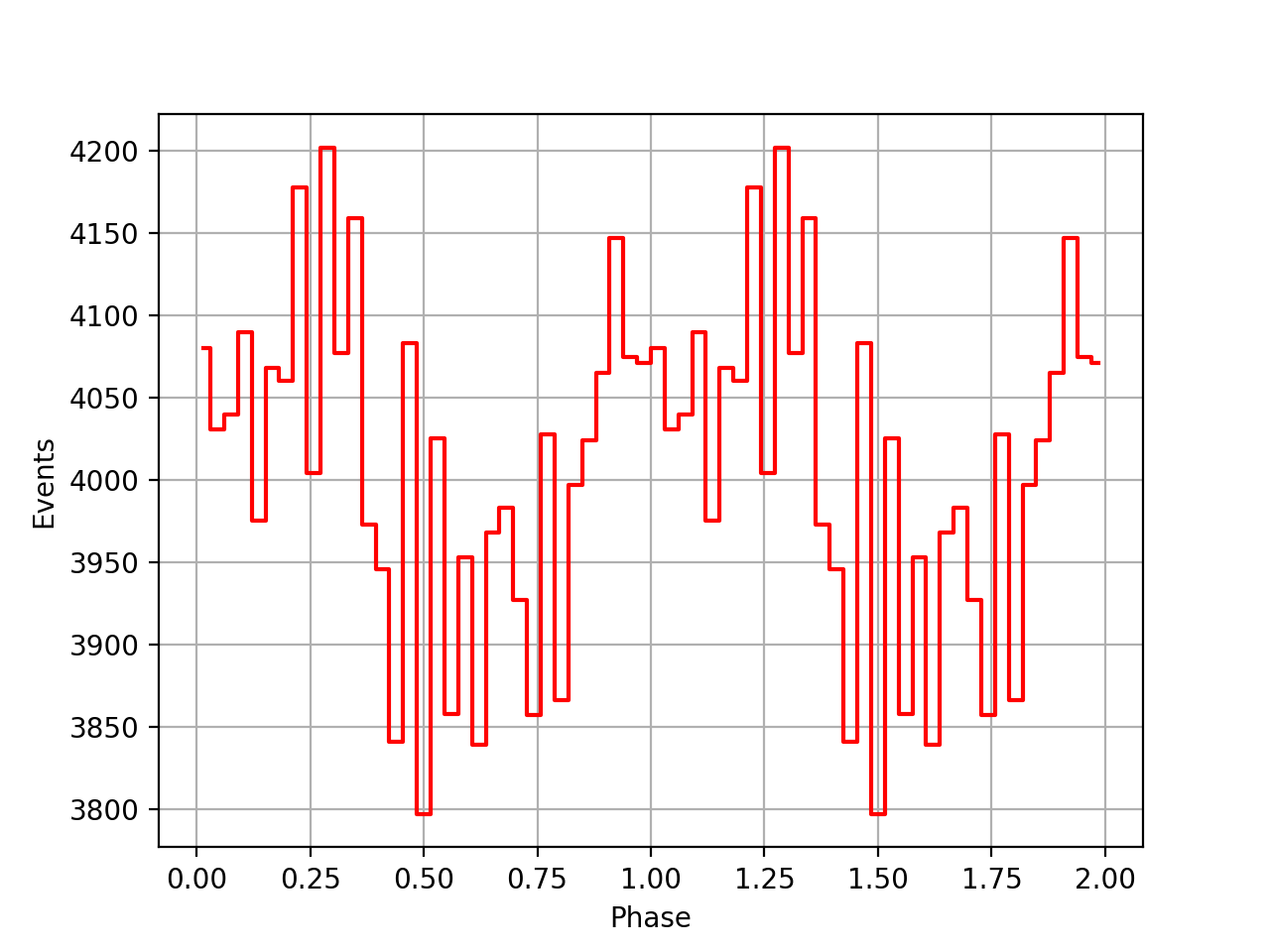 |
±6 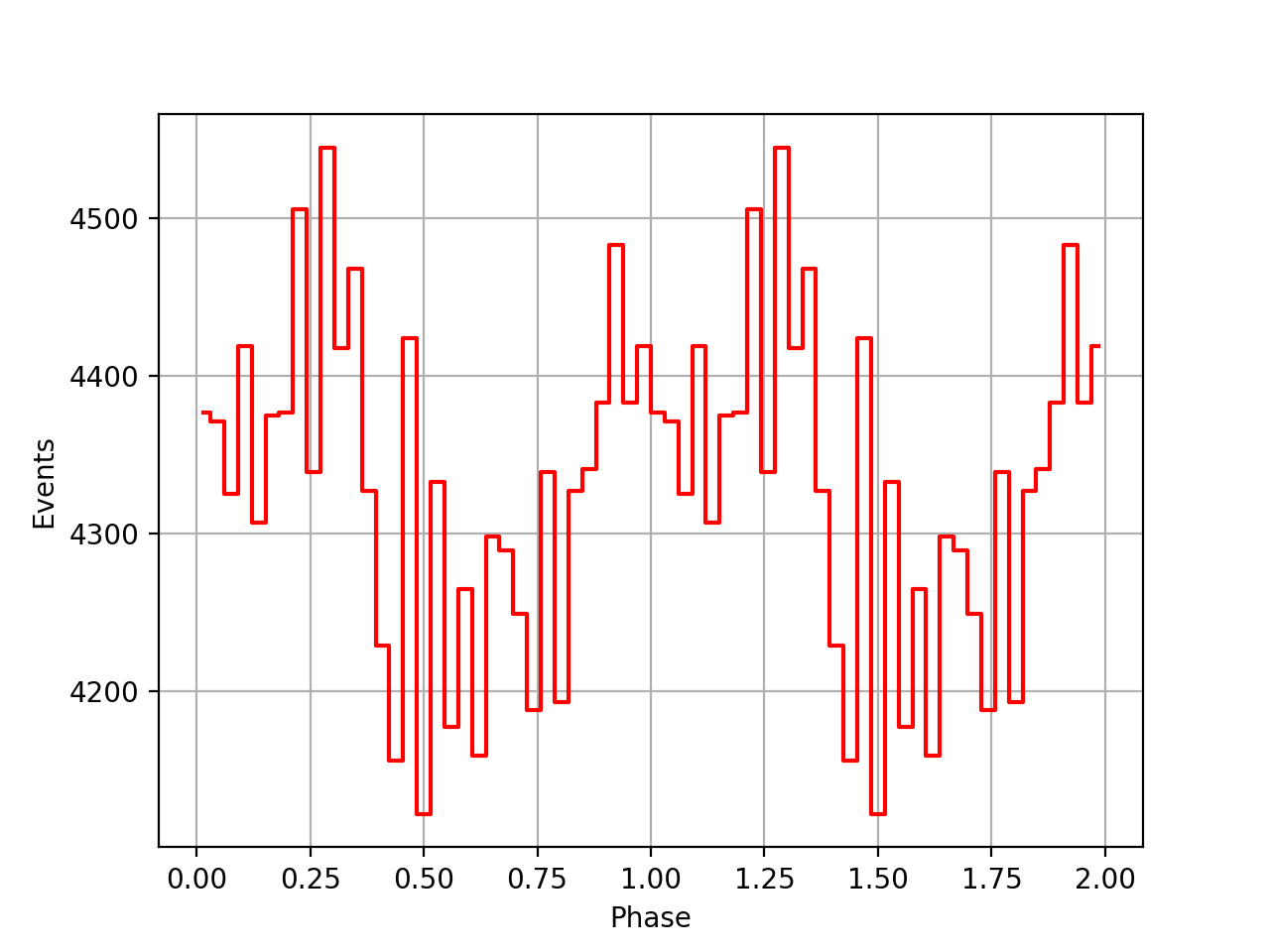 |
#20
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
- File xtereadeph.f added
- File xtebarycen.f added
I found some file and code in the fools that could do the job.
ftools comes with a file de200_new.fits in the reference data that contains the Earth and Sun position based on the JPL DE200 ephmerides for the interval 1972-01-01 to 2049-12-31 (or JD 2436913 to JD 2469807). Each row in the file corresponds to one Julian day. For the Earth, the file contains the position and the first and second position derivatives.
The file xtereadeph.f is some Fortran code to read the file and to interpolate the information to an arbitrary time. The file xtebarycen.f is some Fortran code that applies a Barycentre correction based on the results of xtereadeph.f. Implementing the respective code in GammaLib would enable a on-the-fly Barycentre correction. Alternatively, a Python code could be developed that performs the corrections on some input file to produce a new output file that is used for GammaLib. We should at least implement the second for testing, and if successful, decide whether some code should be implemented in GammaLib.
#21
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
- File pulsar_vp0001_arm3.5.png added
- File pulsar_vp0001_psrtime.ssb.png added
- File pulsar_vp0001_xte_psrtime.png added
- File pulsar_vp0001_xte.psrtime.ssb.png added
- File pulsar_vp0001_jodrell.png added
brycorr.py to apply the JPL DE200 ephemerides for Barycentre correction of the t0geo time. I generated a pulsecurves for VP0001 using different ephemerides:
- The Jodrell Bank CGRO ephemerides for the Crab in the psrtime format. The
t0geois in UTC. - The XTE reference data ephemerides for the Crab in the psrtime format. The time system of
t0geois unknown. - An alternative ephemerides file from Jodrell Bank in a specific format with
t0geoin SSB. The scriptconvert_jodrell.pywas used to convert the input format into an INTEGRAL ephemerides file.
I then used the brycorr.py script to convert the t0 information from the input files, writing the data into an INTEGRAL ephemerides file.
Below the phase curves for the various ephemerides.
Jodrell Bank, CGRO psrtime  |
XTE reference data (psrtime)  |
Jodrell bank SSB 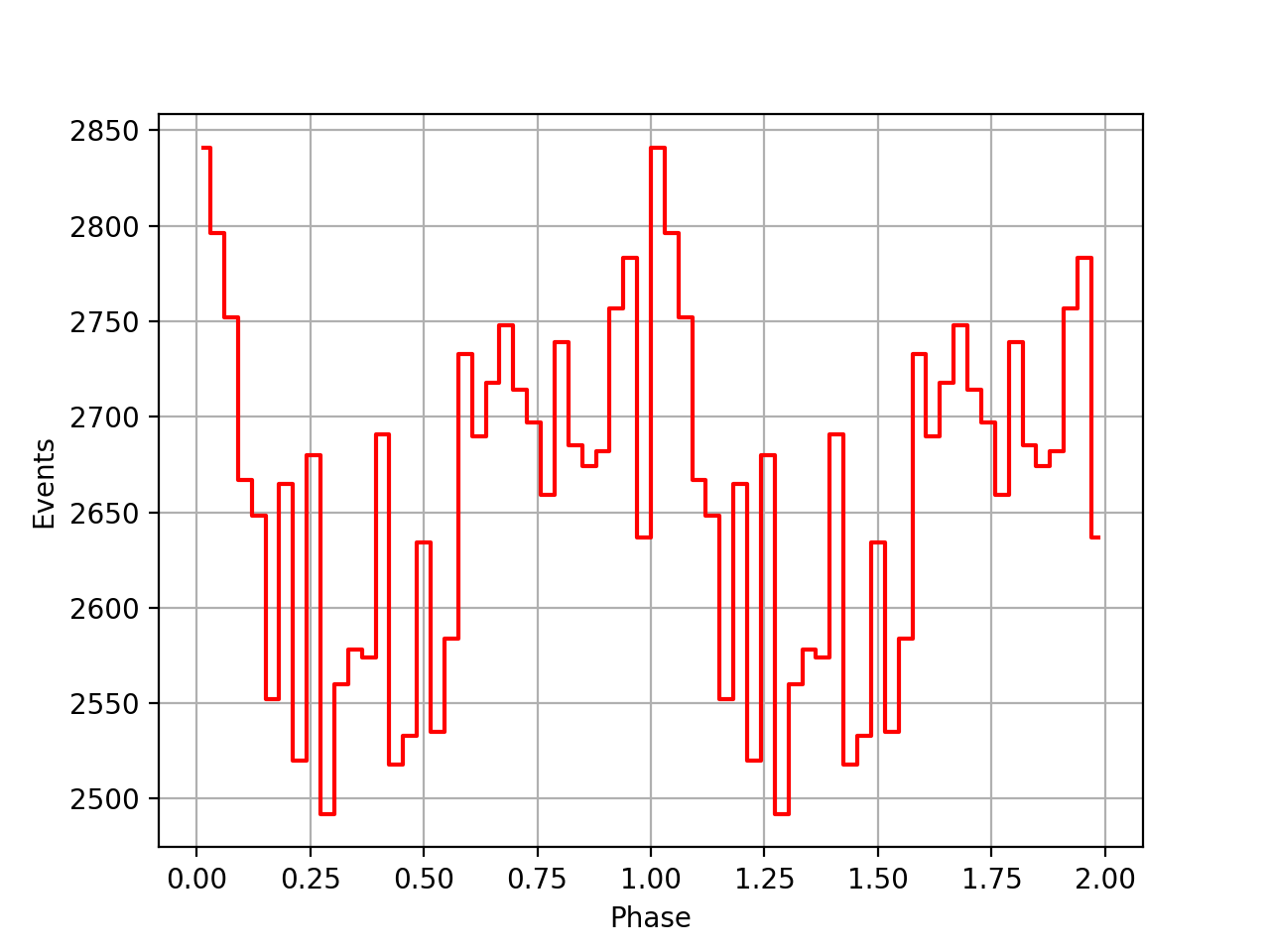 |
Jodrell Bank, SSB corrected CGRO psrtime  |
XTE SSB corrected reference data (psrtime) 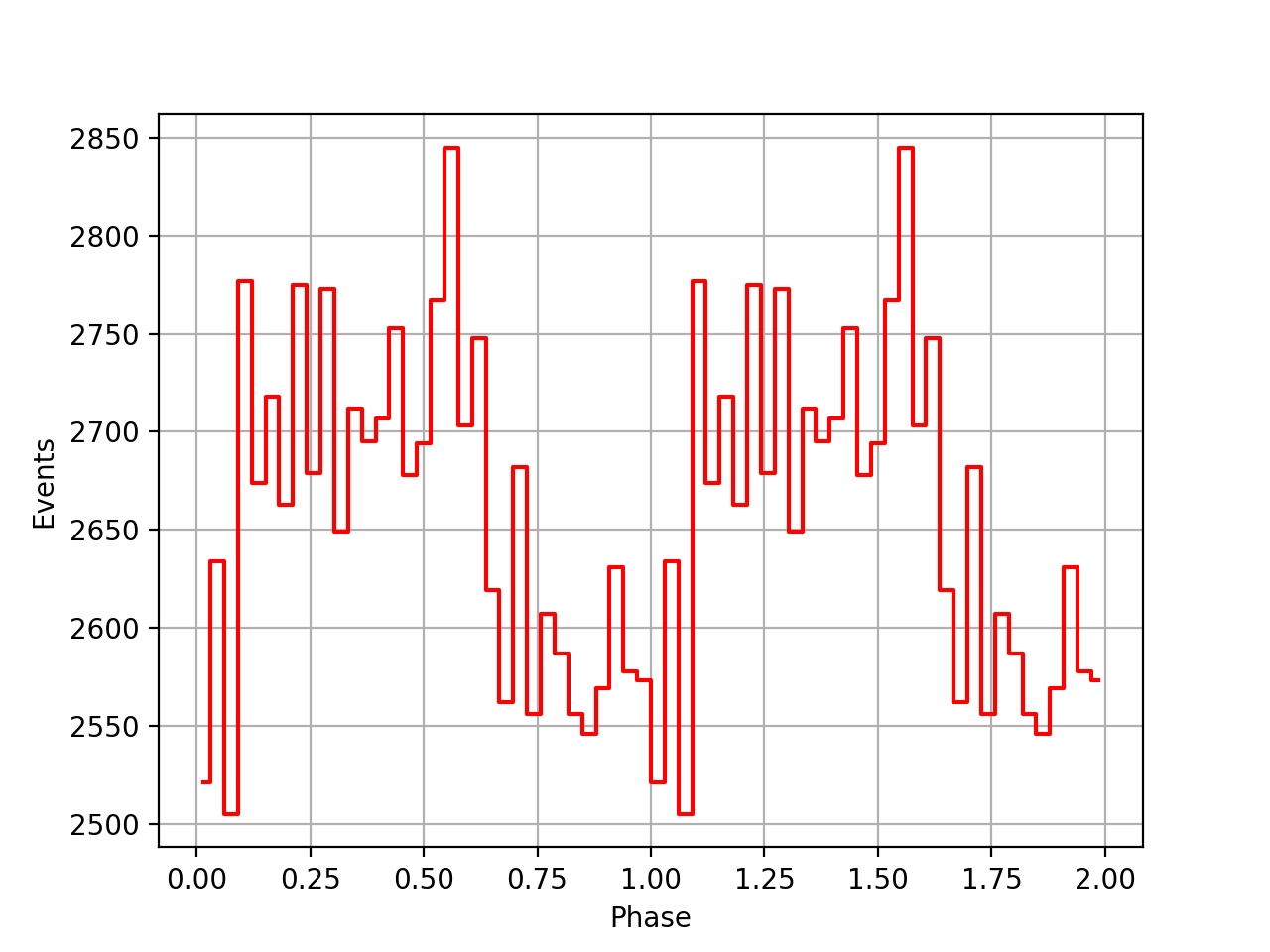 |
#22
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
To make progress I investigated how the INTEGRAL OSA is handling pulsars.
Here some notes from the SPI User Manual:- Ephemeris is provided to the program through a FITS file. In the case of the Crab, one set of ephemeris parameters per month is required to follow the Crab phase over periods much longer than one month. The FITS table includes one ephemeris parameter set in each row with a validity time interval (specified through
MJDSTARTandMJDSTOP). The program can then automatically select a valid ephemeris parameter set (in a given row) for each processed science window. You just have to make sure that the validity intervals encompass the time span of all data included in the analyzed observation group. - We are aware that using a FITS file may be inconvenient for most X-ray pulsars for which only one set of ephemeris parameters is needed.
- The meaning of the ephemeris parameters are standard, and the required information can easily be found trough the WWW.
- Starting with OSA 6.0, the
spi_science_analysisscript offers phased-resolved analysis capabilities.
In the spi_science_analysis.cpp there is the following code:
if (run_phase_analysis == 1) {
status = execute_spiros_phase(spi_science_analysis,
Group,
IRFDOL,
spiros_catalog,
coordinates,
nPhaseBins,
clobber,
chatter);
if (run_phase_analysis == 1) {
status = execute_phase_histogram(spi_science_analysis,
Group,
clobber,
chatter);
These functions are implemented in
ssa_optional_tasks.cpp:ISDCTask spi_phase_hist("spi_phase_hist");
spi_phase_hist["inOG"]=Group;
spi_phase_hist["chatter"]=20;
spi_phase_hist["clobber"]=clobber;
spi_phase_hist["ephemDOL"]="bla";
spi_phase_hist["phaseBinNum"]=20;
spi_phase_hist["phaseSameWidthBin"]="yes";
spi_phase_hist["phaseBounds"]="bla";
spi_phase_hist["phaseSubtractOff"]="no";
spi_phase_hist["phaseOffNum"]=0;
spi_phase_hist["orbit"]="no";
spi_phase_hist["asini"]=0.0;
spi_phase_hist["porb"]=0.0;
spi_phase_hist["T90epoch"]=0.0;
spi_phase_hist["ecc"]=0.0;
spi_phase_hist["omega_d"]=0.0;
spi_phase_hist["pporb"]=0.0;
In this code one can find:
// load ephemeris data valid for the SWG tstart time
Ephem * ephem = new Ephem();
status = ephem->load(tpt->ephemDOL, tstart);
if (status != ISDC_OK) {
RILlogMessage(gRILFileRef, Error_2,
"Error %d in loading ephemeris file %s", status, tpt->ephemDOL );
continue;
} else {
RILlogMessage(gRILFileRef, Log_2,
" Ephemeris loaded: ScW TSTART: %16.11f - ref time: %6.1f = %3.1f days",
tstart, ephem->tref0, (tstart - ephem->tref0));
if( tpt->chatter > 50 ) { ephem->dump(); }
}
// compute barycentric times for all events
status = events->baryCalc(swg, *ephem, evtType_max);
if (status != ISDC_OK) {
RILlogMessage(gRILFileRef, Error_2,
"%d : Error converting evt IJD to barycentric time",
status);
continue;
}
// compute orbital correction if applicable
if ( tpt->orbit ) {
anEvtPtr->orbiTime(*tpt);
} else {
anEvtPtr->setOrbi(anEvtPtr->bary());
}
// compute the event phase
phase = anEvtPtr->phase(swg, *ephem);
and the called methods are reading as follows:
/*----------------------------------------------------------------------------*/
/* Evt::baryTime((dal_element * swg, Ephem const & ephem) */
/* -------------------------------------------------------------------------- */
/* Return the barycentric time of the event */
/*----------------------------------------------------------------------------*/
double Evt::baryTime(dal_element * swg, Ephem const & ephem)
{
int status = ISDC_OK;
_bary = _time;
status = DAL3AUXconvertBarycentIJD(swg, 1, ephem.srcRA, ephem.srcDEC,
DAL3AUX_TDB, DAL3AUX_ANY, TCOR_ANY,
&_bary, status);
if (status != ISDC_OK) {
RILlogMessage(gRILFileRef, Error_2,
"%d : Error converting evt IJD to barycentric time",
status);
return -1.0;
}
return _bary;
}
/*----------------------------------------------------------------------------*/
/* Evt::orbiTime(Parameters const & tpt) */
/* -------------------------------------------------------------------------- */
/* Return the time of the event corrected for orbital motion */
/*----------------------------------------------------------------------------*/
double Evt::orbiTime(Parameters const & tpt)
{
int status = ISDC_OK;
double time = _bary;
double asini = tpt.asini;
double porb = tpt.porb;
double T90epoch = tpt.T90epoch;
double ecc = tpt.ecc;
double omega_d = tpt.omega_d;
double pporb = tpt.pporb;
if (porb==0){
porb=1e-10;
}
if (ecc>=1){
ecc=0.999999;
}
if (ecc<0){
ecc=0;
}
double asini_d = asini/86400.0;
double twopi = 2.0*3.1415927;
double t = time;
double omega=omega_d*3.1415927/180.0;
double sinw=sin(omega);
double cosw=cos(omega);
for (int i=0;i<6;i++){
double t1=t-T90epoch;
double m=twopi*(
t1/porb-0.5 *pporb*t1*t1/porb/porb)
+3.1415927/2.0-omega;
double eanom=m;
for(int j=0;j<5;j++){
eanom=eanom-(eanom-ecc*sin(eanom)-m)/(1.0-ecc*cos(eanom));
}
double sin_e=sin(eanom);
double cos_e=cos(eanom);
double z=asini_d*(sinw*(cos_e-ecc)+sqrt(1.0-ecc*ecc)*cosw*sin_e);
double dz=twopi*asini_d/porb/(1.0-ecc*cos_e)*
(sqrt(1.0-ecc*ecc)*cosw*cos_e-sinw*sin_e);
double f=t+z-time;
double df=1.0+dz;
if (df==0){
df=1e-10;
}
t=t-f/df;
}
_orbi = t;
return _orbi;
}
/*----------------------------------------------------------------------------*/
/* Evt::phase(Ephem const ephem) */
/* -------------------------------------------------------------------------- */
/* Return the event detector number (pseudo det number if multiple) */
/*----------------------------------------------------------------------------*/
double Evt::phase(dal_element * swg, Ephem const & ephem)
{
// deltaT = time (in seconds) betwwen phase zero next to reference time and
// event time corrected for barycentric and for orbital motions if any
double deltaT = 86400.0 * ( _orbi - ephem.tref0 ) - ephem.t2peak0;
// Number of turns during delatT
double Turns = ephem.freq0 * deltaT + ephem.fdot0 * deltaT * deltaT/2.0 +
ephem.fdotdot0 * deltaT * deltaT * deltaT/6.0;
_phase = (Turns - floor(Turns));
return _phase;
}
This indicates that
double deltaT = 86400.0 * ( _orbi - ephem.tref0 ) - ephem.t2peak0 which is equivalent with double deltaT = 86400.0 * _orbi - (86400.0 * ephem.tref0 ) + ephem.t2peak0), hence the reference time is a simple addition of the reference MJD multiplied by the number of seconds in one day plus the time to peak, as done in GPulsar.#23
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
I checked whether there may be some issue with the precision of GTime at typical MJD times of CGRO:
# Check GTime precision at the beginning of CGRO observtion (start of VP0001)
>>> print(gammalib.GTime('MJD 48392.10000000')-gammalib.GTime('MJD 48392.00000000'))
8639.99999988 <=> 8640 (-1.19209289551e-07)
>>> print(gammalib.GTime('MJD 48392.01000000')-gammalib.GTime('MJD 48392.00000000'))
864.000000119 <=> 864 (1.19209289551e-07)
>>> print(gammalib.GTime('MJD 48392.00100000')-gammalib.GTime('MJD 48392.00000000'))
86.3999996185 <=> 86.4 (-3.81469732247e-07)
>>> print(gammalib.GTime('MJD 48392.00010000')-gammalib.GTime('MJD 48392.00000000'))
8.63999974728 <=> 8.64 (-2.52723694416e-07)
>>> print(gammalib.GTime('MJD 48392.00001000')-gammalib.GTime('MJD 48392.00000000'))
0.864000201225 <=> 0.864 (2.01225280771e-07)
>>> print(gammalib.GTime('MJD 48392.00000100')-gammalib.GTime('MJD 48392.00000000'))
0.0864000320435 <=> 0.0864 (3.20434570267e-08)
>>> print(gammalib.GTime('MJD 48392.00000010')-gammalib.GTime('MJD 48392.00000000'))
0.00864005088806 <=> 0.00864 (5.08880615233e-08)
>>> print(gammalib.GTime('MJD 48392.00000001')-gammalib.GTime('MJD 48392.00000000'))
0.000863671302795 <=> 0.000864 (-3.2869720459e-07)
>>> print(gammalib.GTime('MJD 48392.000000001')-gammalib.GTime('MJD 48392.000000000'))
8.60691070557e-05 <=> 0.0000864 (-3.30892944336e-07)
# Check GTime precision for one tic at the beginning of CGRO observations
>>> print(gammalib.com_time(8392,1)-gammalib.com_time(8392,0))
0.000125050544739
>>> print(gammalib.com_time(8392,1)-gammalib.com_time(8392,0)-0.000125)
5.05447387695e-08
# Check GTime precision for one tic at the end of CGRO observations
>>> print(gammalib.com_time(11690,1)-gammalib.com_time(11690,0))
0.000124990940094
>>> print(gammalib.com_time(11690,1)-gammalib.com_time(11690,0)-0.000125)
-9.05990600586e-09
3.8e-7 s which corresponds to 0.38 micro seconds. This precision should be largely sufficient for pulsar timing. In any case it is much better than the length of one tic, which is 0.000125 s or 125 micro seconds. Hence times in GTime should not be a problem.#24
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
- File pulsar_vp0001_psrtime.png added
- File pulsar_vp0001_psrtime2integral.png added
- File pulsar_vp0001_psrtime2fermi.png added
Here is a verification that an ephemeris specified in the psrtime format gives the same results as the same ephemeris specified in the INTEGRAL and Fermi formats. This does not mean that an INTEGRAL or Fermi ephemeris is correctly used, but it demonstrates that the interface works as expected.
t0 in the interfaces. Here is what is currently done:
psrtime-t0.mjd(t0geo)- INTEGRAL -
t0.mjd(tref0->real(i))followed byt0 += t2peak->real(i) - Fermi -
t0.mjd(toabary_int->integer(i)+toabary_frac->real(i))
psrtime 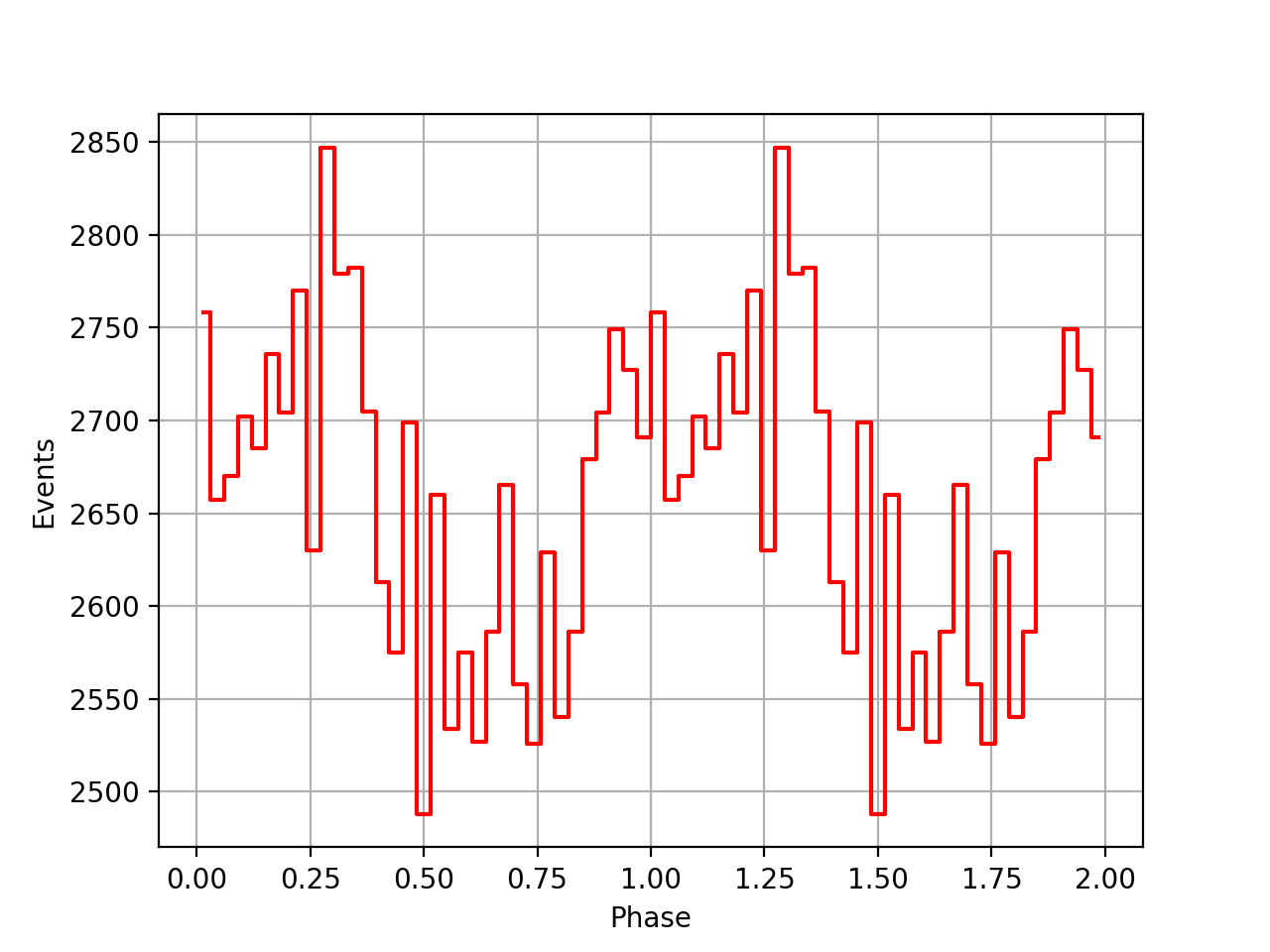 |
INTEGRAL  |
Fermi  |
#25
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
- File pulsar_vp0001_psrtime.png added
- File pulsar_vp0001_psrtime.ssb_v2.png added
- File pulsar_vp0337_psrtime.png added
- File pulsar_vp0337_psrtime.ssb.png added
- File pulsar_vp0616_psrtime.png added
- File pulsar_vp0616_psrtime.ssb.png added
I concentrate now on the Crab CGRO ephemerides in psrtime format as found at http://www.jb.man.ac.uk/~pulsar/crab/all.gro.
I ran compulbin on three viewing periods to look at the resulting phasecurves. The table below specifies the viewing periods, as well as the corresponding ephemeris from the Crab CGRO psrtime file. Note that VP0616 is covered by two lines in the psrtime file.
| Viewing period | MJDSTART | MJDSTOP | Line | Valitidy | t0geo | f0 | f1 | f2 | rms | obs |
| VP0001 | 48392.903 | 48406.786 | 53 | 48377-48407 | 48392.000000224 | 29.9485663280898 | -3.77641D-10 | 0.00D+00 | 1.5 | J |
| VP0337 | 49573.978 | 49593.569 | 92 | 49565-49595 | 49580.000000222 | 29.9098677334486 | -3.76400D-10 | 1.52D-20 | 0.3 | J |
| VP0616 | 50497.934 | 50525.603 | 123 | 50480-50508 | 50494.000000144 | 29.8801798033427 | -3.75514D-10 | -4.50D-20 | 1.8 | J |
| 124 | 50509-50538 | 50523.000000040 | 29.8792388788960 | -3.75524D-10 | 2.34D-21 | 0.7 | J |
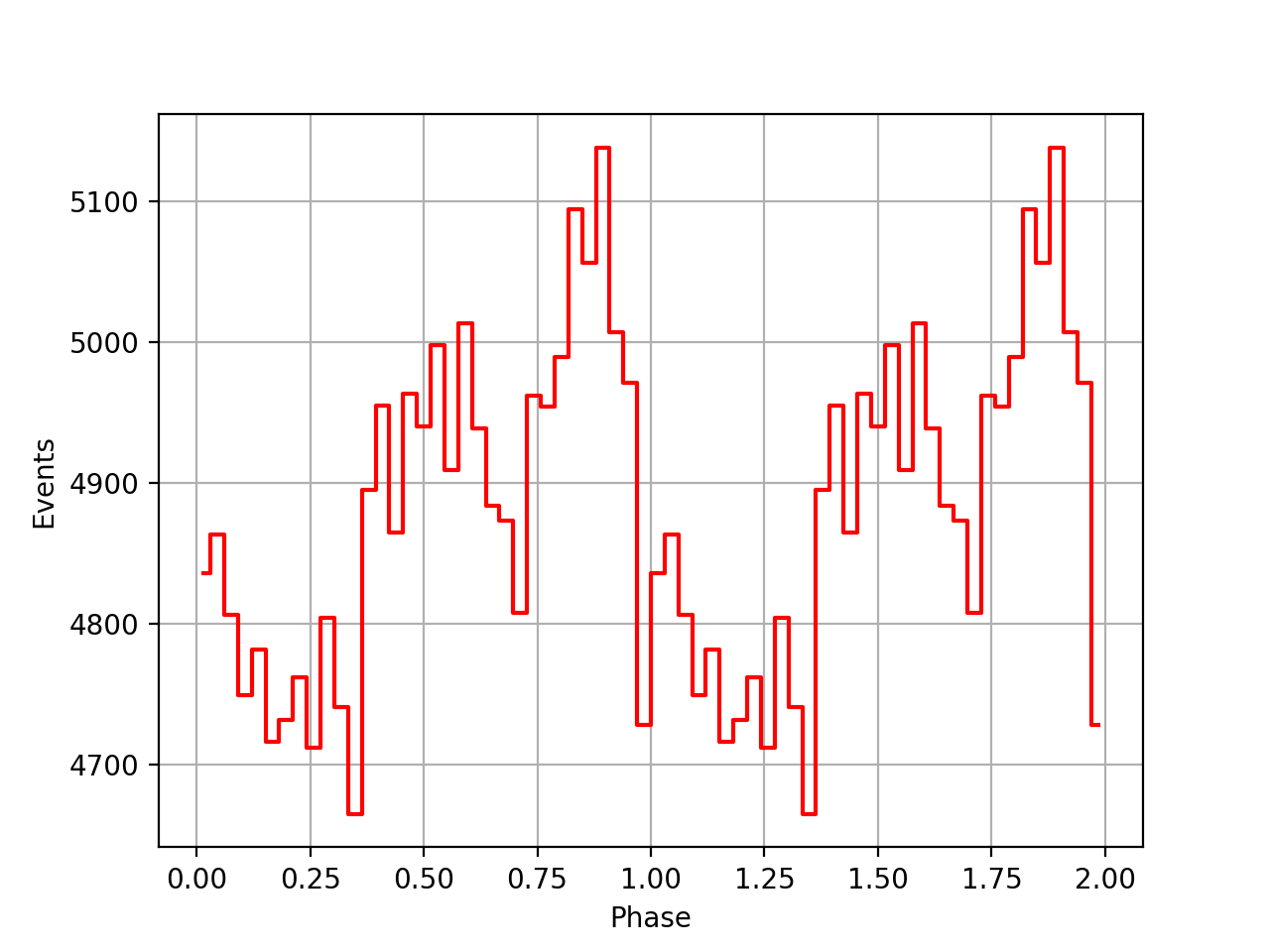
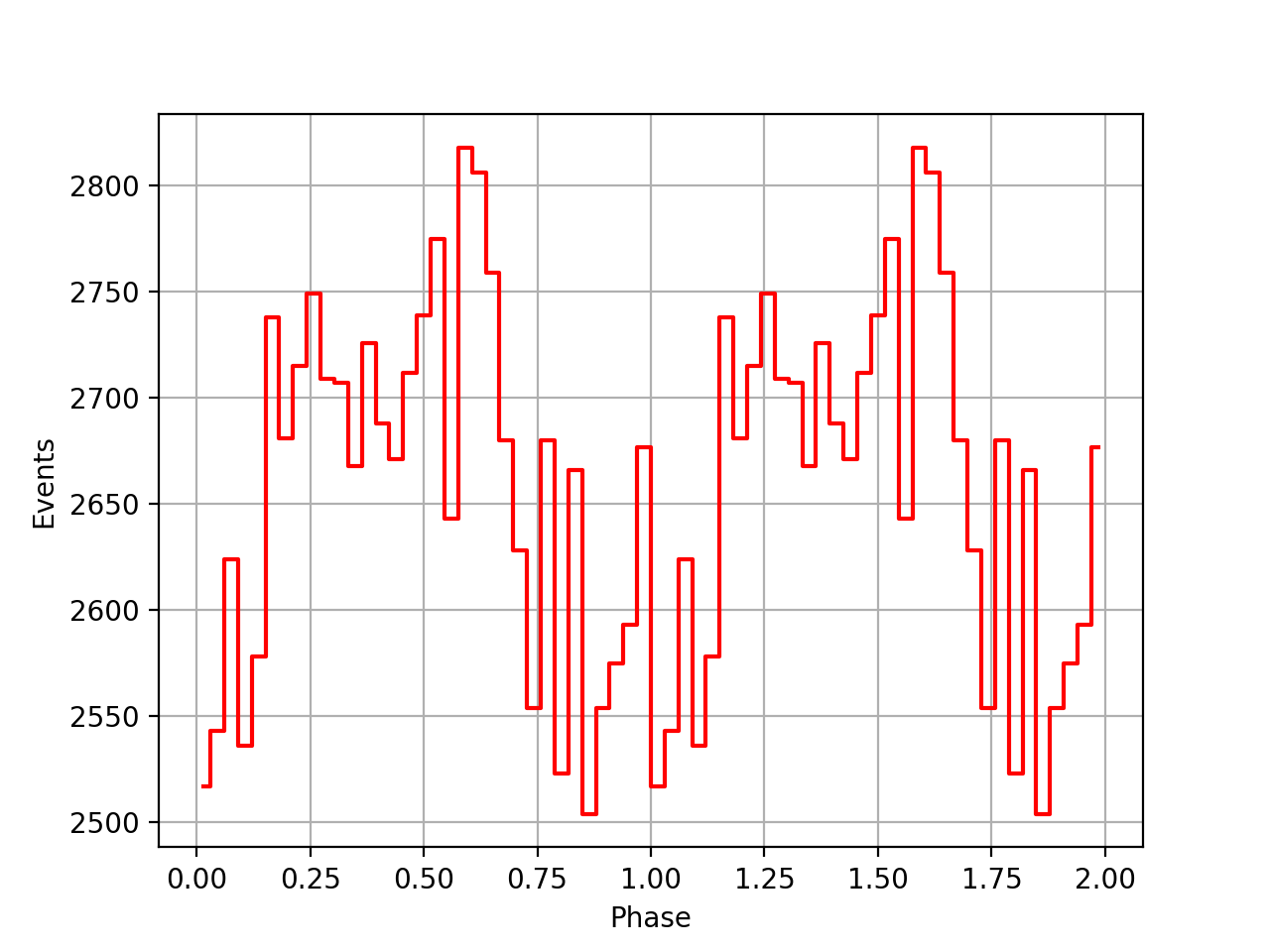
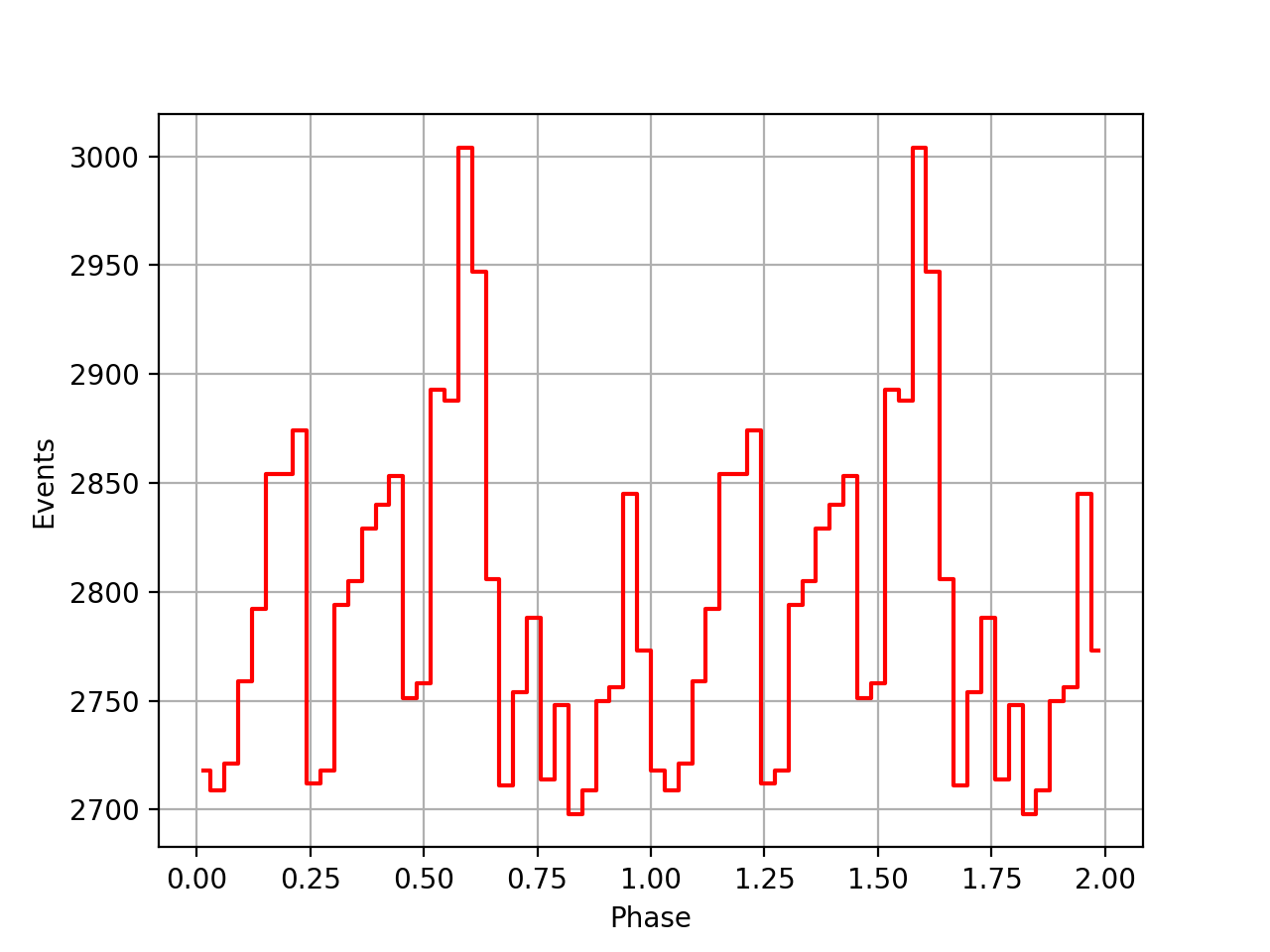
The images below show the phasecurves. The top row shows the phasecurves obtained with the ephemeris from the psrtime file, using
t0nom = float(int(t0geo.mjd()))
time2peak = (t0geo.mjd() - t0nom) * gammalib.sec_in_day
t0geo into t0ssb usingtcorr = ephemerides.barycor(t0geo, srcdir)
t0sbb = t0geo + tcorr
t0nom = float(int(t0geo.mjd()))
time2peak = (t0sbb.mjd() - t0nom) * gammalib.sec_in_day
| VP0001 | VP0337 | VP0616 |
 |
 |
 |
 |
 |
 |
#26
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
- File pulsar_vp0001_psrtime.ssb.20220112T1500.png added
- File pulsar_vp0337_psrtime.ssb.20220112T1500.png added
- File pulsar_vp0616_psrtime.ssb.20220112T1500.png added
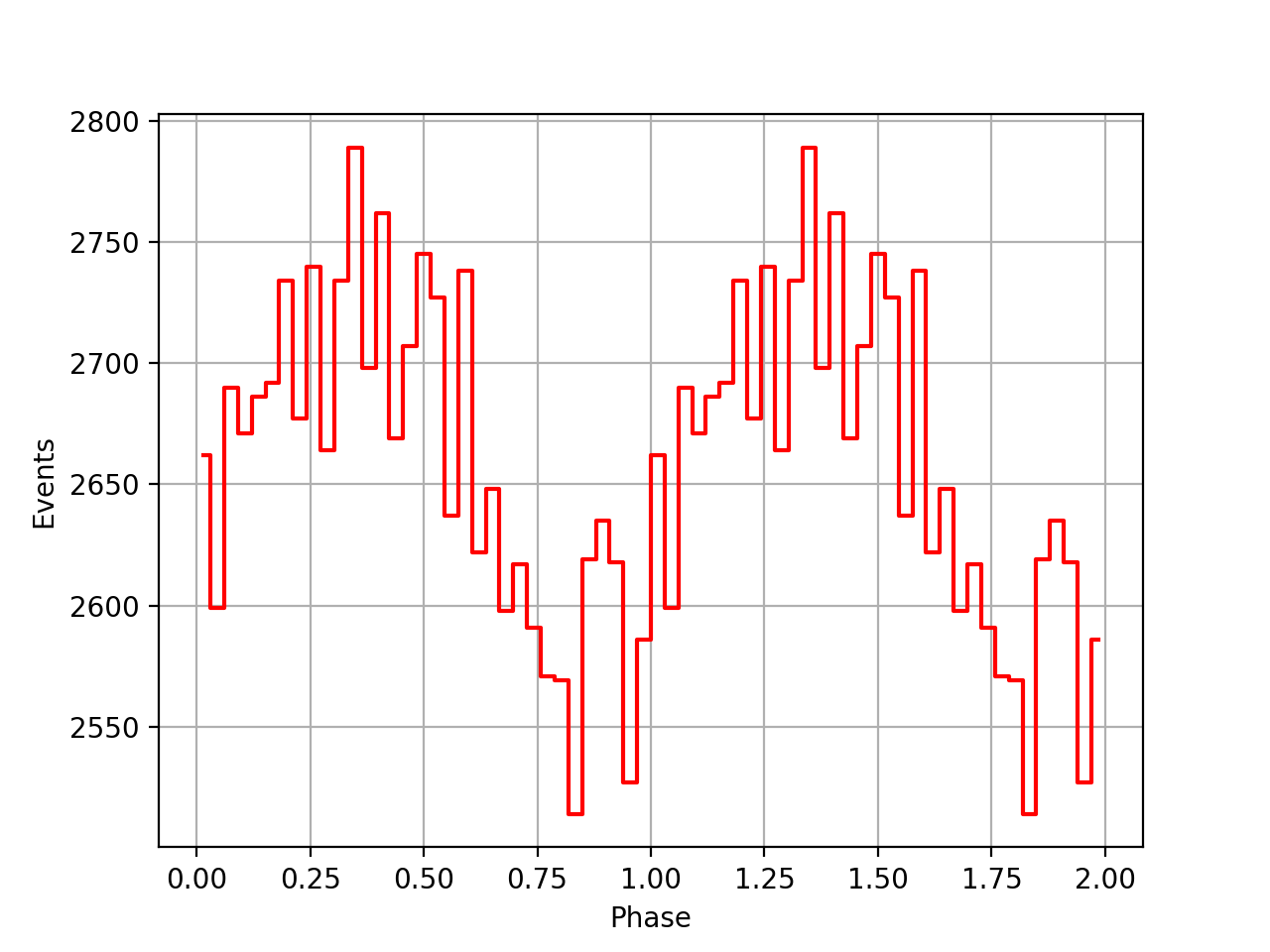
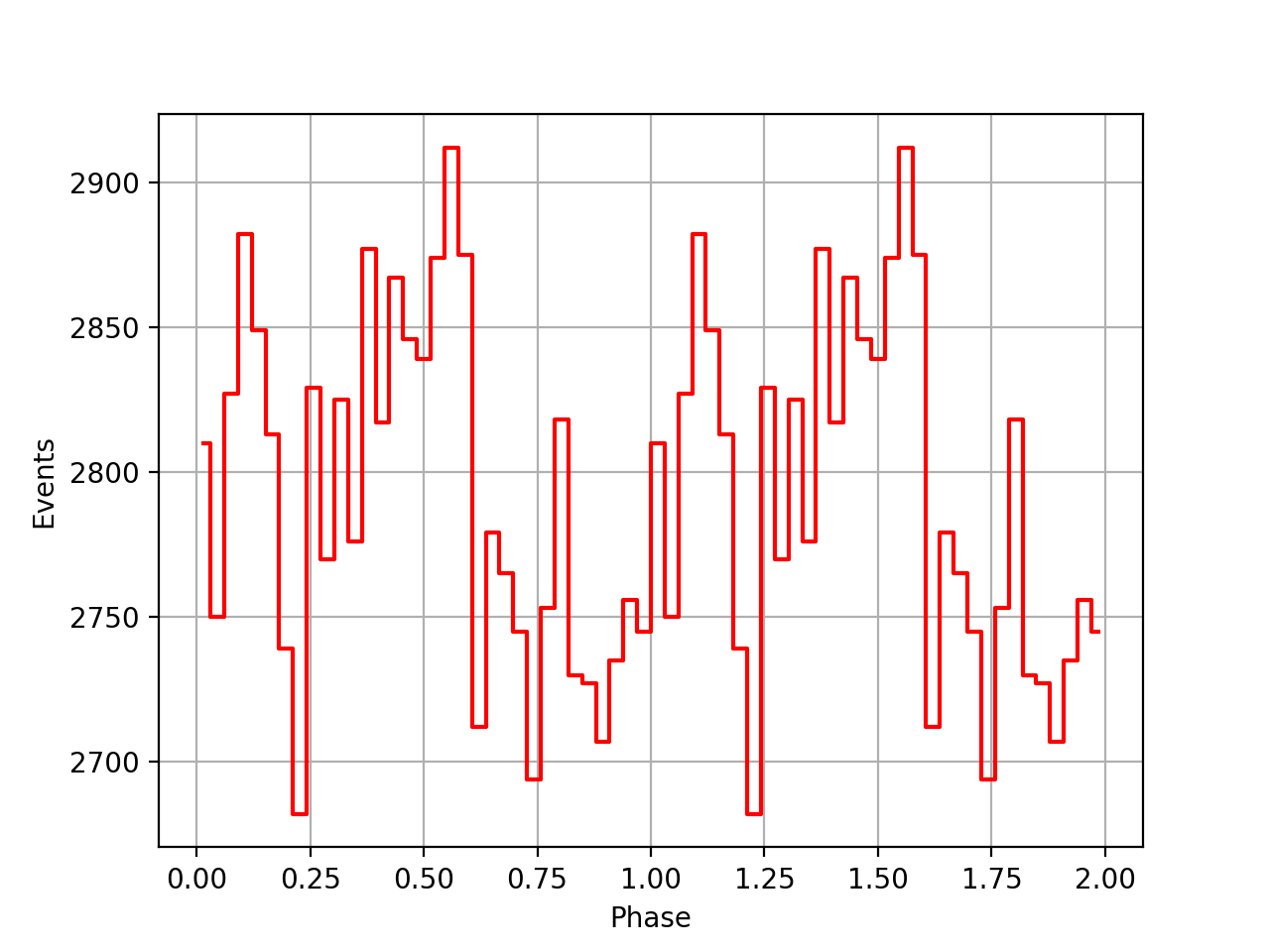
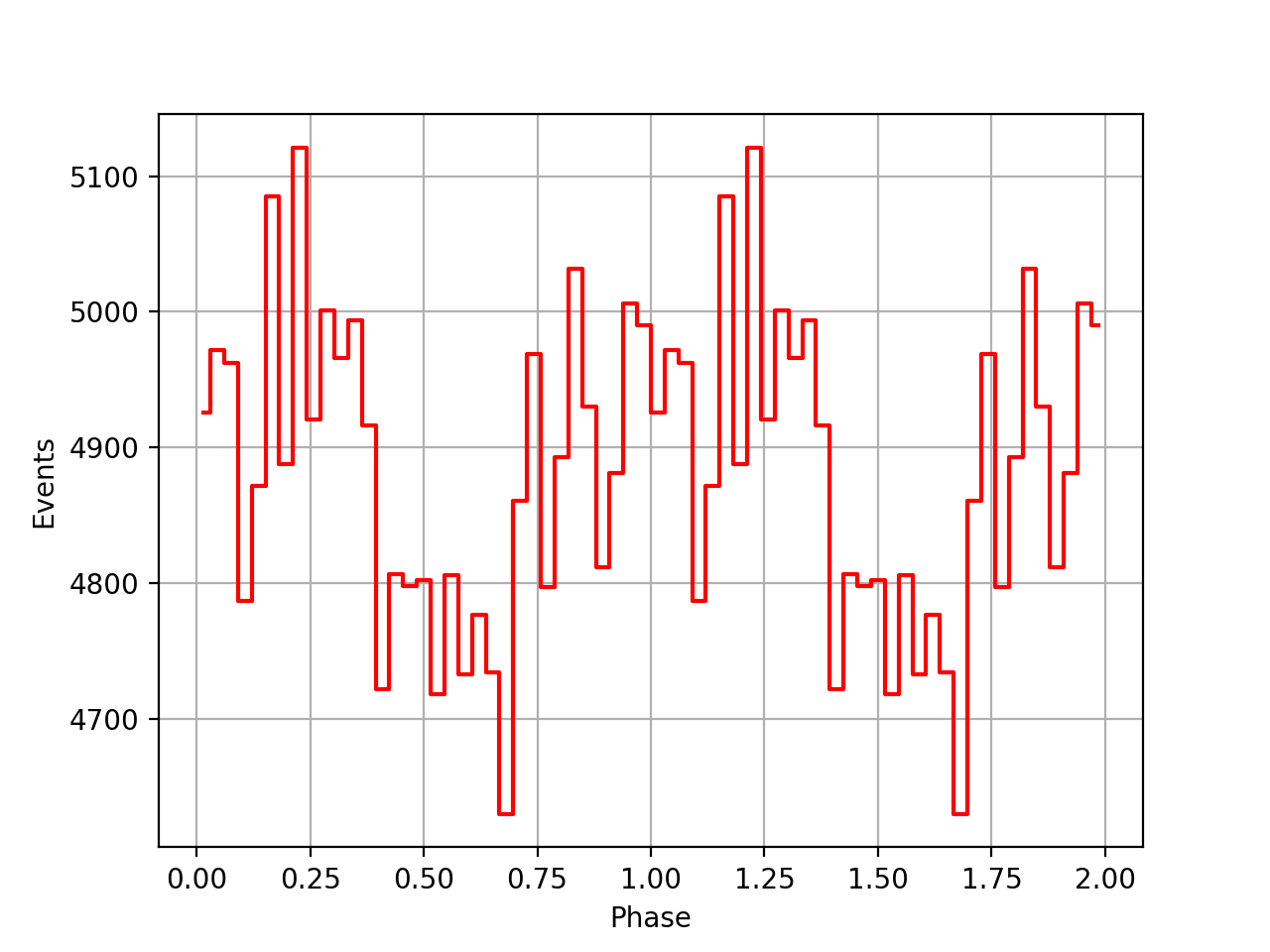
There was an error in the time derivative computation of ETUT in my barycor script, where the time derivative had the wrong sign. After correction, the following SSB corrected phasecurves were obtained. The phasecurves are still not aligned.
| VP0001 | VP0337 | VP0616 |
 |
 |
 |
#27
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
- File pulsar_vp0001_jodrell_20220112T1622.png added
- File pulsar_vp0337_jodrell_20220112T1622.png added
- File pulsar_vp0616_jodrell_20220112T1622.png added
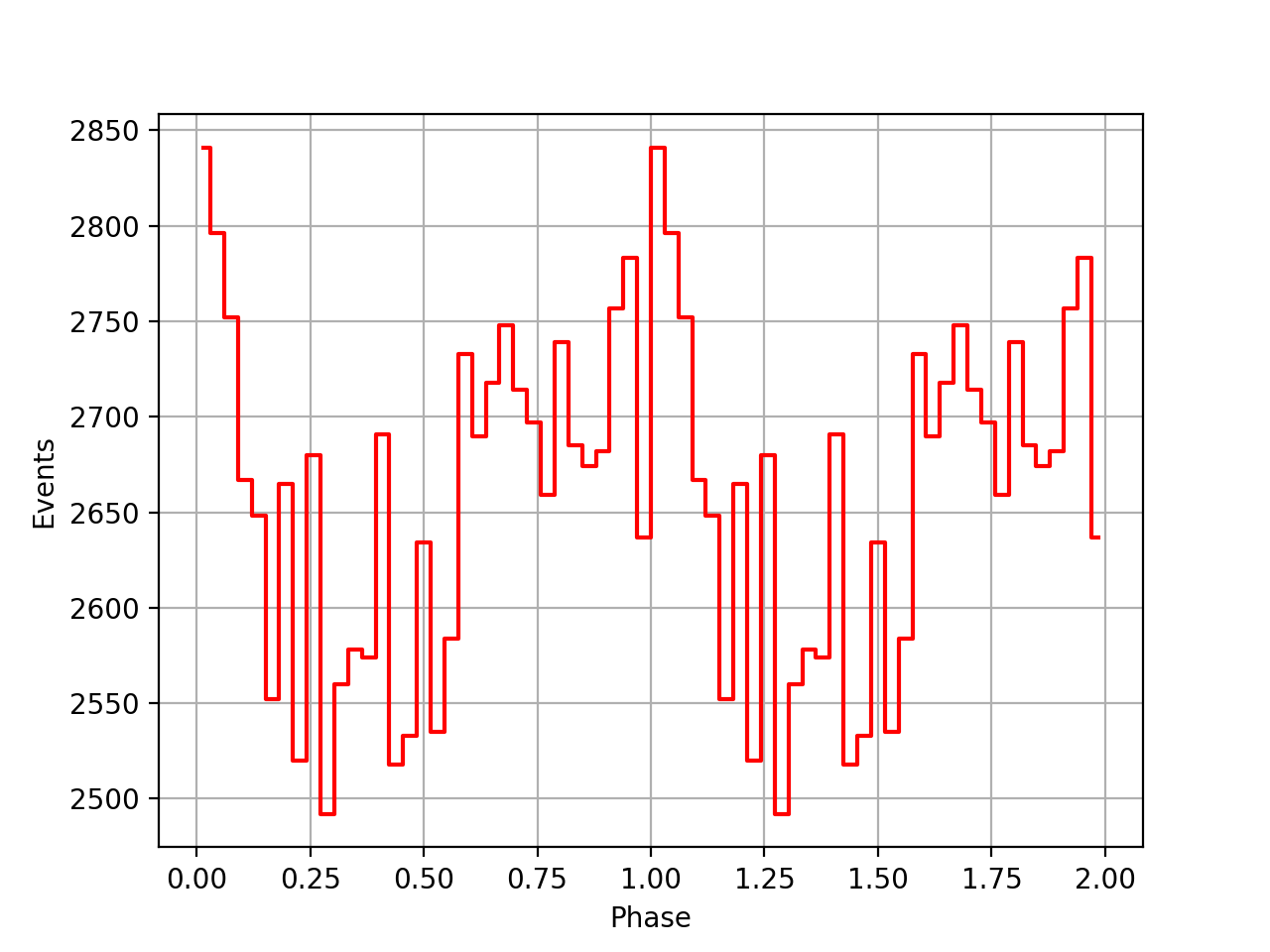
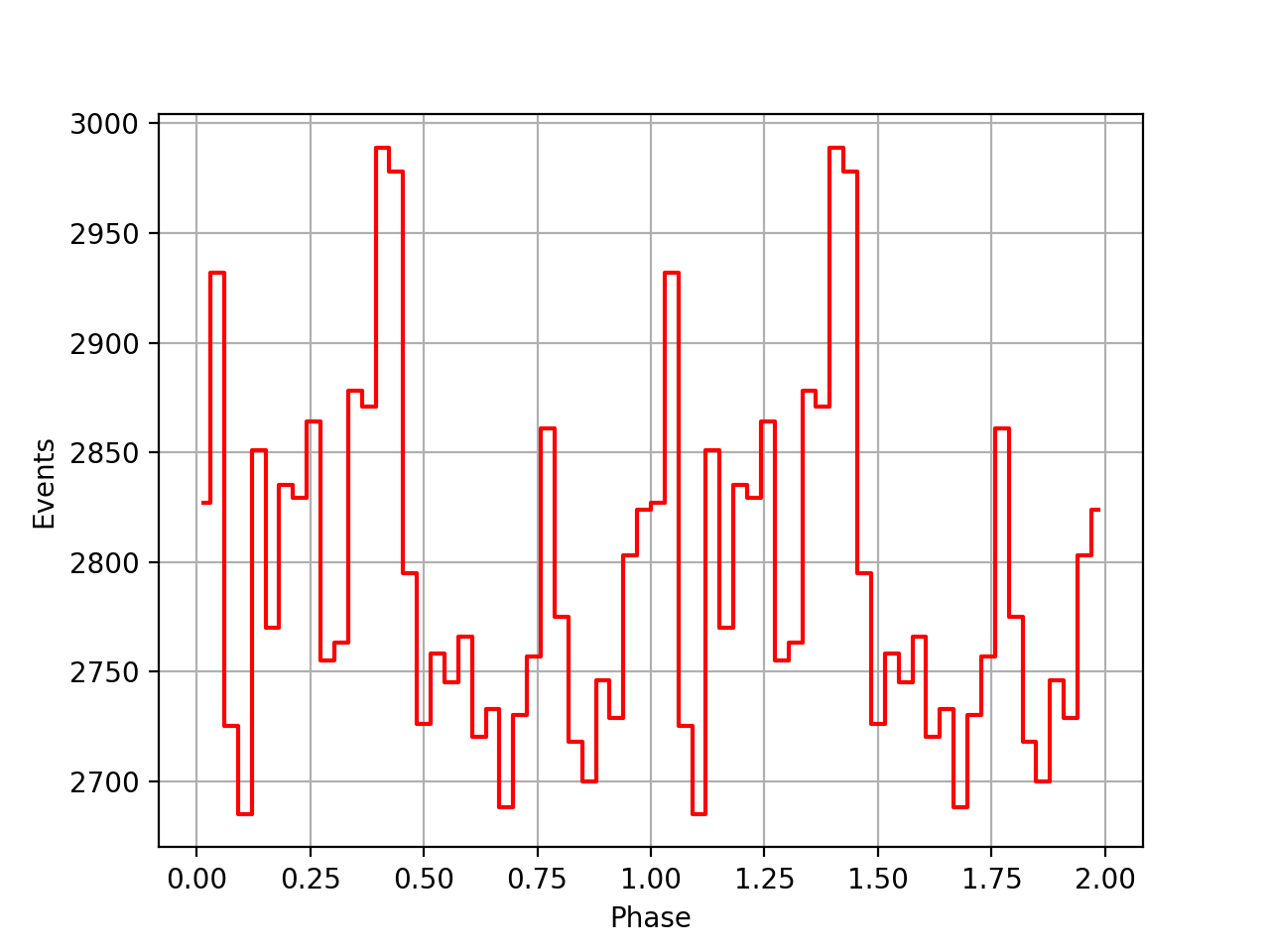
Below the same kind of comparison for the Jodrell Bank ephemeris which are a-priori already with a reference time in the SSB frame:
The arrival times given are those of the centre of the first main pulse after midnight at infinite frequency at the barycentre of the solar system, in seconds. The timescale is now quoted in terms of T.D.B. To convert to T.A.I. 32.184 seconds must be subtracted, as well as the gravitational clock correction. t_JPL is the barycentric arrival time obtained using the JPL (DE200) ephemeris (Standish 1982).
| VP0001 | VP0337 | VP0616 |
 |
 |
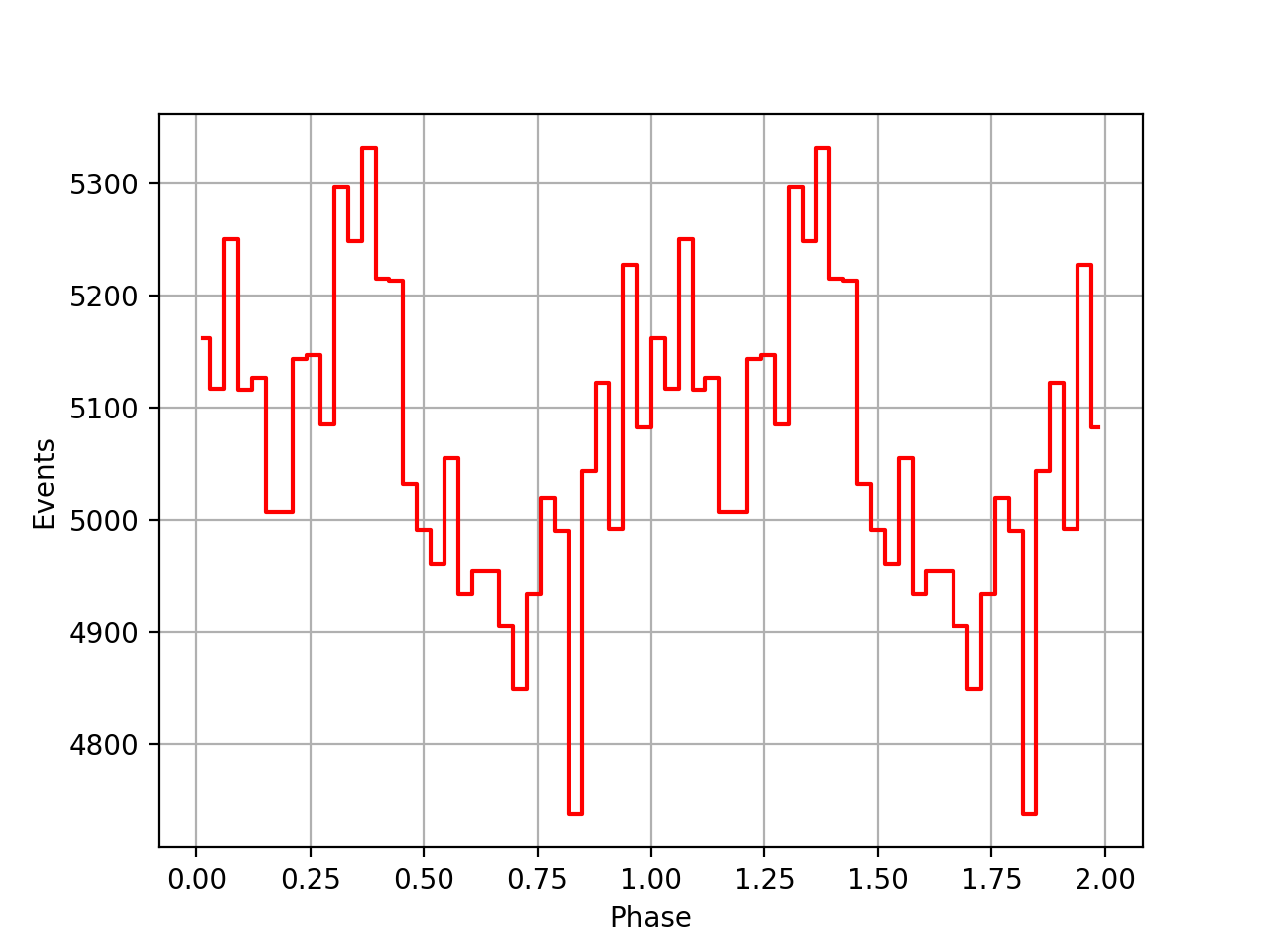 |
#28
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
I now compared the Barycentre correction in barycor.py to the one done in GCOMBvcs::tdelta. For line 53 in the psrtime file, which corresponds to VP0001, the
| Parameter | barycor.py |
GCOMBvcs::tdelta |
| MJD | 48392.000000224 | 48392.9 |
| tdelta | -380.795625 | -384.585 |
| travel | -438.980839 | -442.77 |
| Shapiro | 0.000020 | 2.0827e-05 |
| Etut | 58.185235 | 58.1852 |
The times for which the evaluation was done is not exactly the same, which may explain why travel is not identical. Yet the agreement seems to be reasonable for about one day of difference. Note also the CGRO is not at the geocentre.
#29
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
- File pulsar_vp0001_psrtime.ssb.20220112T1739.png added
- File pulsar_vp0337_psrtime.ssb.20220112T1739.png added
- File pulsar_vp0616_psrtime.ssb.20220112T1739.png added
- File pulsar_vp0001_jodrell_20220112T1748.png added
- File pulsar_vp0337_jodrell_20220112T1748.png added
- File pulsar_vp0616_jodrell_20220112T1748.png added
I implemented a computation where the reference epoch t0 is only the integral part of t0geo and the phase is computed using
const double c1 = 1.0/2.0; const double c2 = 1.0/6.0; double dt = t0geo - double(int(t0geo)) * gammalib::sec_in_day; double phase = (f0 + (f1 * c1 + f2 * dt * c2) * dt) * dt; phase -= floor(phase);
This results in the following phase curves. The top row is for the CGRO SSB corrected psrtime file, the bottom row is for the Jodrell Bank psrtime file that is already SSB corrected. Not sure that this is any better.
| VP0001 | VP0337 | VP0616 |
 |
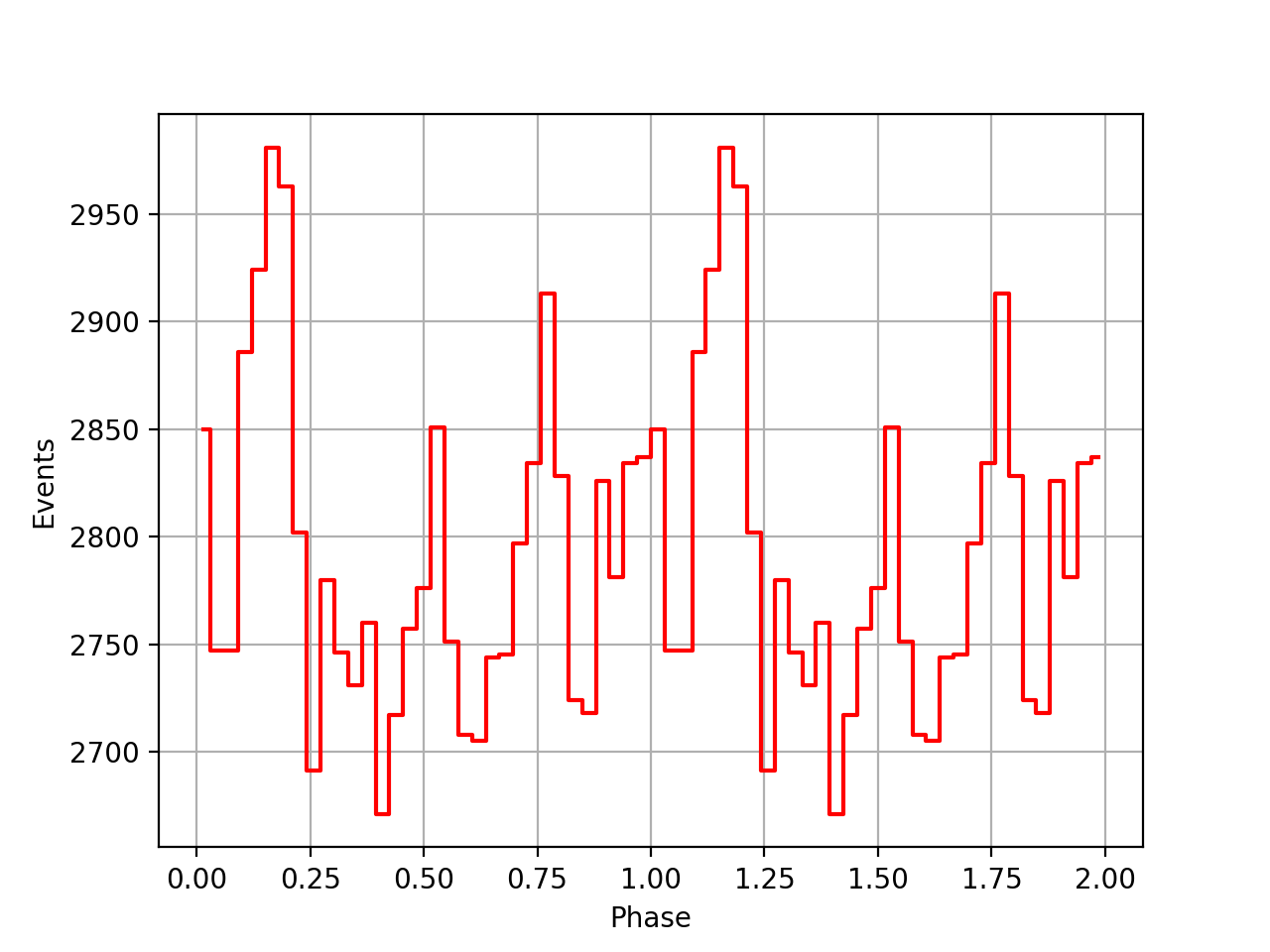 |
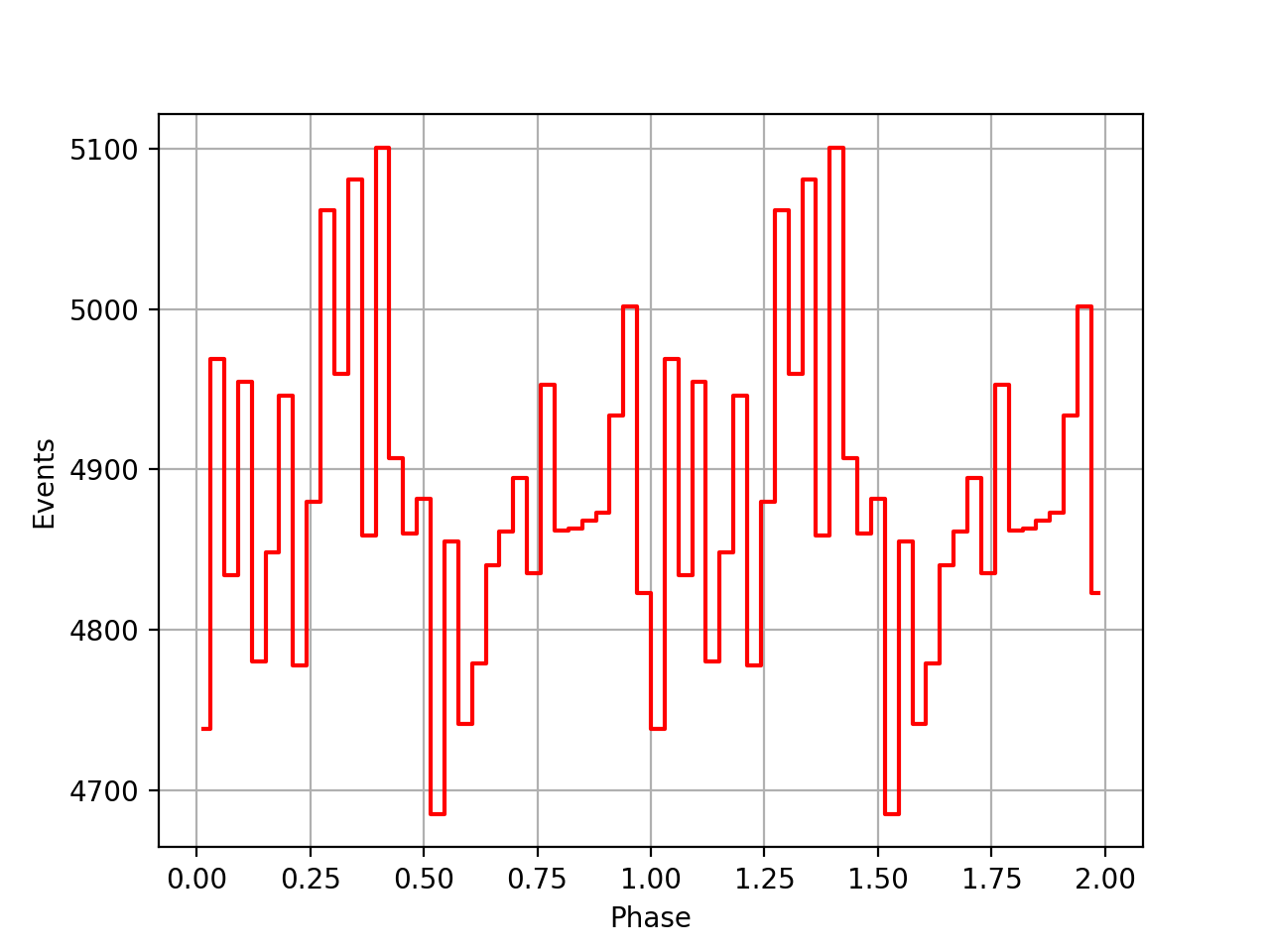 |
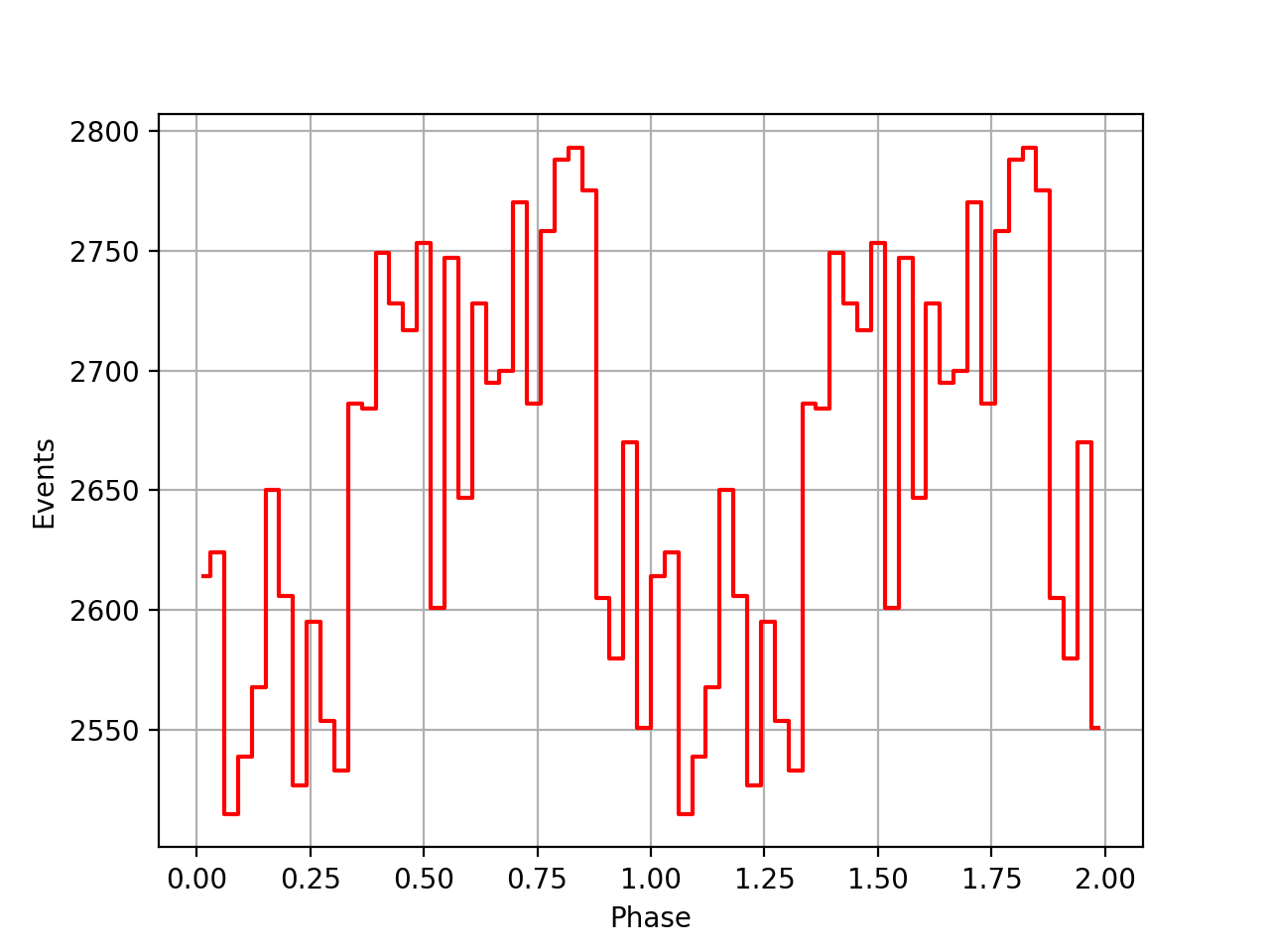 |
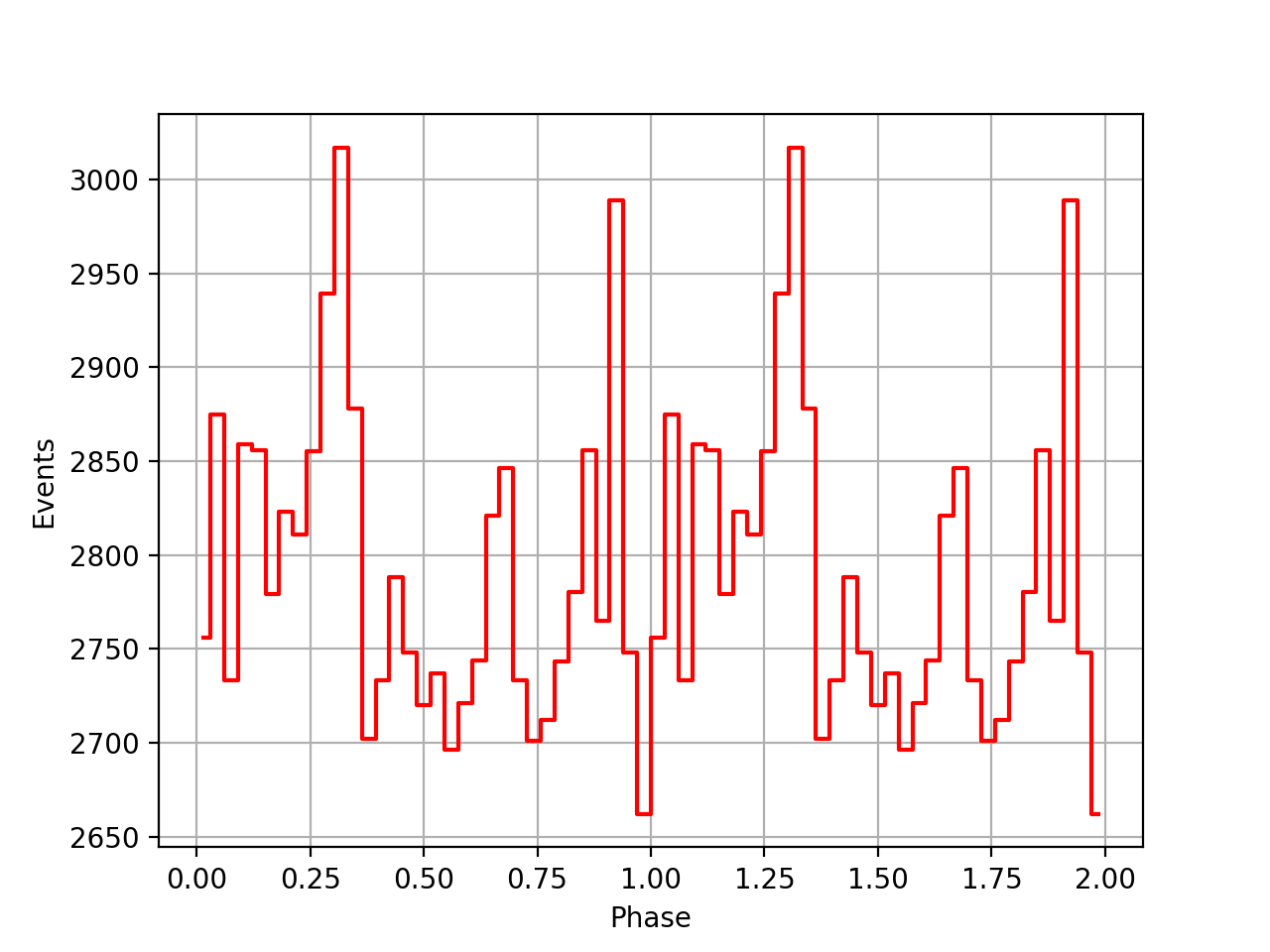 |
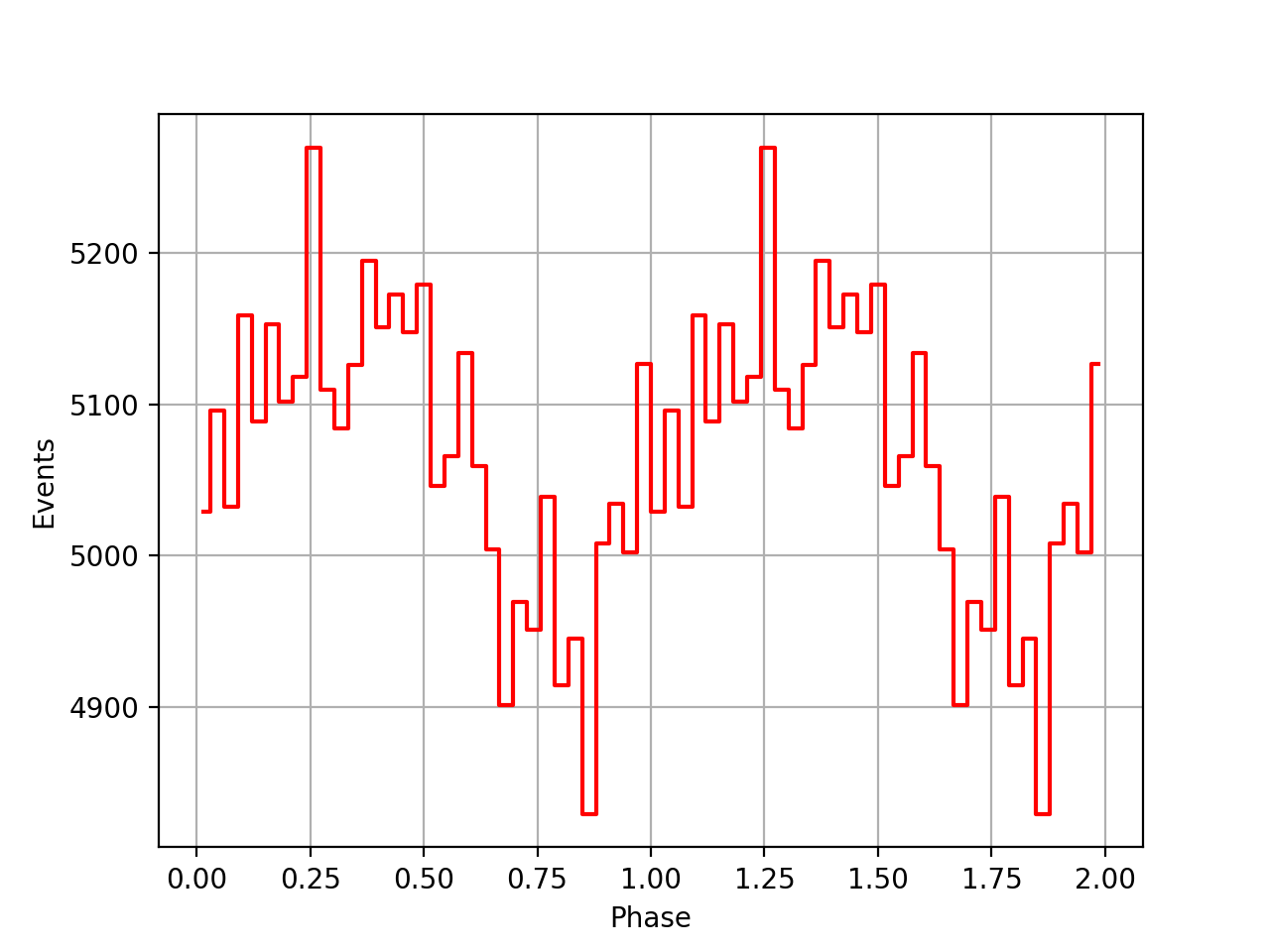 |
#30
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
Maybe this code from the ftools/axBary tasks that is found in bary.c has some relevance:
timeparams
// Read line from PSRTIME file
timeline (line, bsource, &ra, &dec, &mjd1, &mjd2, &mjdi, &mjdf, &fd, &dfd, &ddfd, &dddfd, &rms, &fbin, &tdenum, jsource) ;
// Stuff
ptp->f = fd ; // f0
ptp->df = dfd ; // f1
ptp->ddf = ddfd ; // f2
ptp->dddf = dddfd ; // f3
i = mjdf * 100.0 + 0.5 ; // Keep the first 3 digits of the fractional part,
mjdftrun = (double) i / 100.0 ; // ... drop the others (copes with 48499.999999517 style dates)
ptp->t0.MJDint = mjdi ; // MJD integer part
ptp->t0.MJDfr = mjdftrun ; // MJD fractional part (should be 0 or 1)
ptp->t0.ts = TDB ; // Time system (SSB)
// Convert UTC to TT
mtime.MJDint = mjdi ;
mtime.MJDfr = mjdf + roffset / SECDAY ; // roffset: extra offset to be applied to radio zero phase (in s)
mtime.ts = UTC ;
toTT (&mtime) ; // Converts UTC->TT (i.e. adds leap seconds + 32.184), mtime.ts = TT on output
tr = barycorr (&mtime, dir, scposn0) ;
dtt = tr + ( (mtime.MJDint - ptp->t0.MJDint) + (mtime.MJDfr - ptp->t0.MJDfr) ) * SECDAY ;
ptp->radioph = -fd*dtt - dfd*dtt*dtt*0.5 - ddfd*dtt*dtt*dtt/6.0 - dddfd*dtt*dtt*dtt*dtt/24.0 ;
// TDB-TT = tr
// DT (=Tr-T0) = dtt
// Phase(T0) = ptp->radioph
Note that the
radioph (which is probably the radio phase) is negative.#31
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
- File 2017_Yan_arXiv1708.05898-Phase-evolution.pdf added
Note that this paper 2017_Yan_arXiv1708.05898-Phase-evolution.pdf is interesting in this respect since it also has the radio phase computed from Jodrell Bank as negative phase in the computation of the Nanshan phase (Equations 3 and 4).
Note also that bary.h defines
typedef struct {
double ra ; /* RA */
double dec ; /* Dec */
int denum ; /* JPL ephemeris number */
MJDTime t0 ; /* reference epoch (in MJD(TDB)(at barycenter)) */
double f ; /* pulsar frequency */
double df ; /* pulsar frequency derivative */
double ddf ; /* pulsar frequency second derivative */
double dddf ; /* pulsar frequency third derivative */
double radioph ; /* radio phase at reference epoch */
} PsrTimPar ;
#32
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
- File pulsar_vp0001_psrtime_20220113T2303.png added
- File pulsar_vp0001_psrtime_20220113T2304.png added
The Solar System Barycentre time correction returned by obs.bvcs().tdelta(ephemeris.dir(), time) includes the UTC→TT term, which is the number of leap seconds plus 32.184 s. This term however is only required if the times are in UTC. It is not fully clear whether COMPTEL times are in UTC or TT (or something else), yet UTC would not be very natural for a satellite time due to the handling of leap seconds.
Below two phasecurves for VP0001 derived using the uncorrected psrtime ephemerides. The left was derived using the original code (where the UTC→TT term is added), the right was derived using the code
# Convert event time to Solar System Barycentre time
time = event.time()
tdelta = obs.bvcs().tdelta(ephemeris.dir(), time)
utc_to_tdt = time.secs('TT') - time.secs('UTC') # TODO: Check
time = time + tdelta - utc_to_tdt # TODO: Check
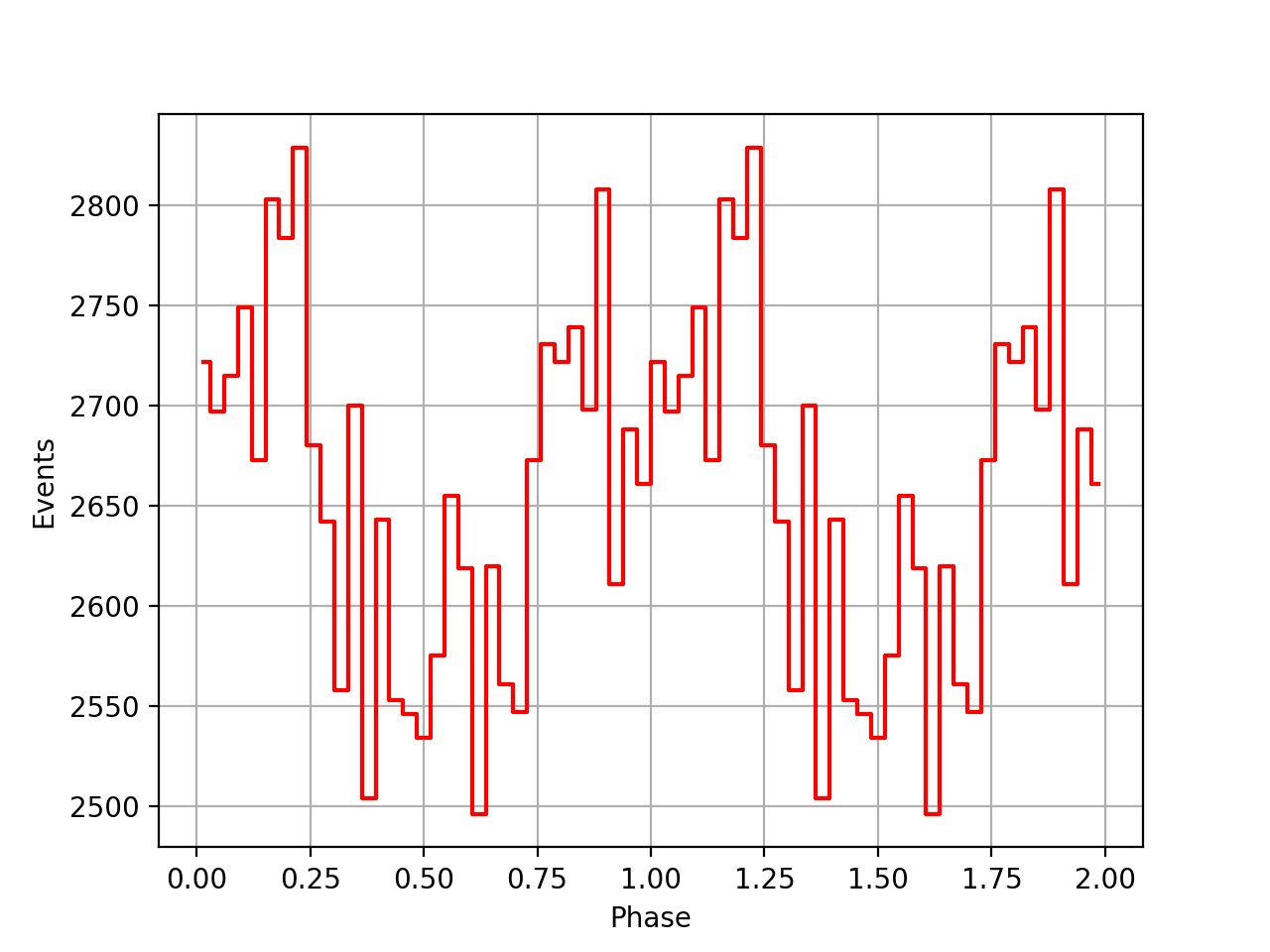 |
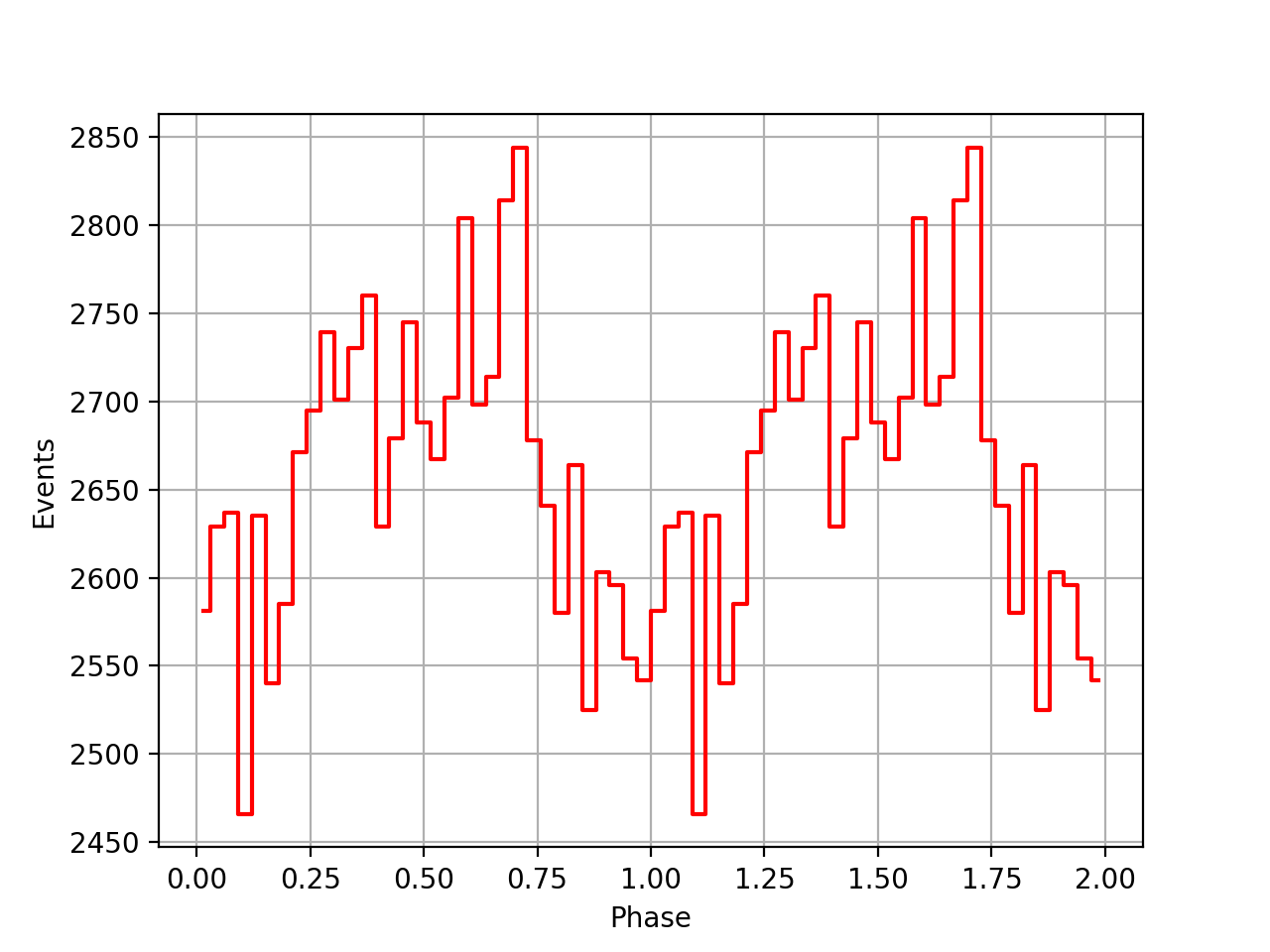 |
#33
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
- File pulsar_vp0001_psrtime_20220113T2351.png added
- File pulsar_vp0337_psrtime_20220113T2351.png added
- File pulsar_vp0616_psrtime_20220113T2351.png added
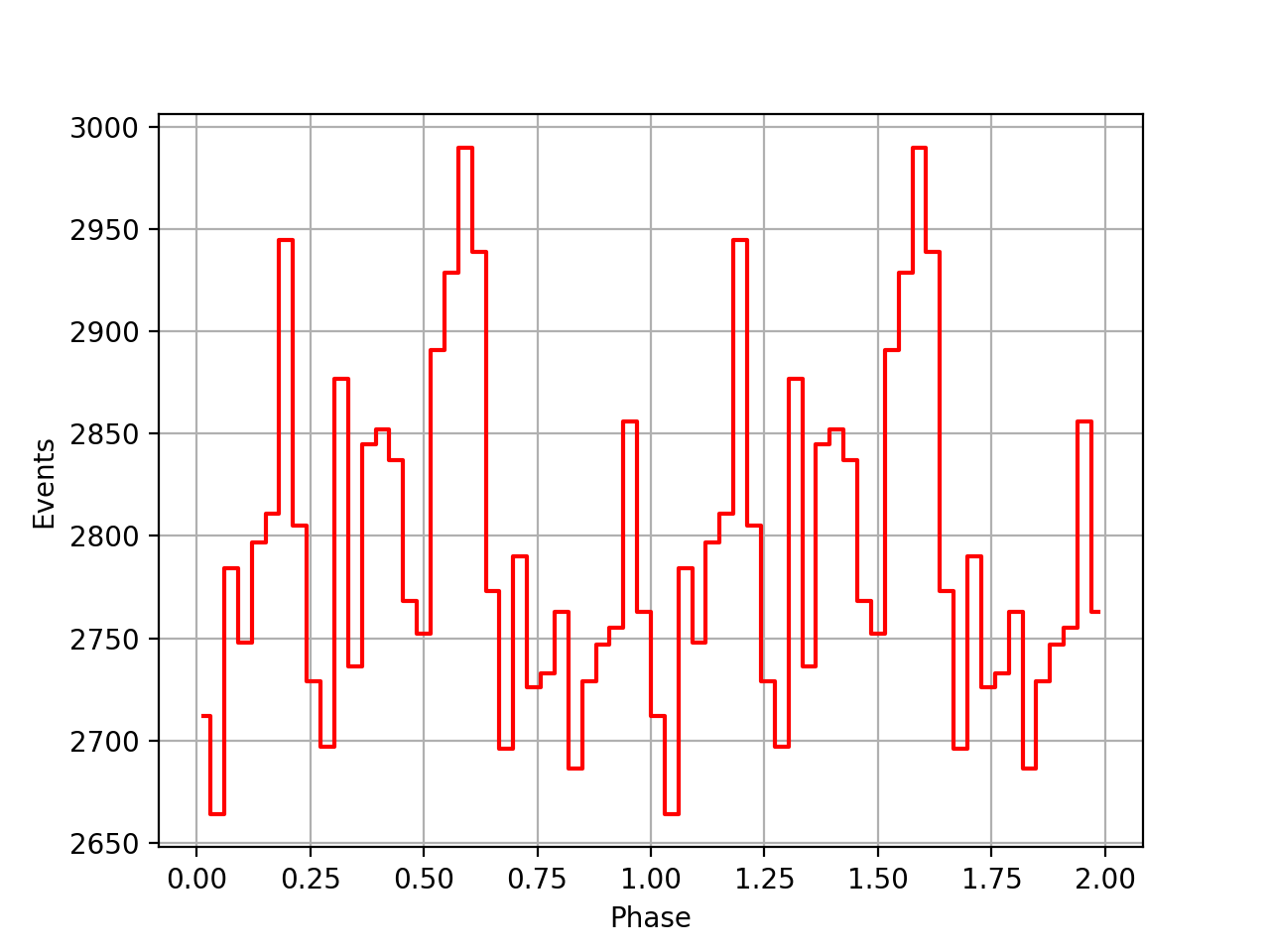
- % Done changed from 50 to 60
I implemented a GEphemerides class to deal with the JPL DE200 ephemerides in the code. Here a first try of using this class for an on-the-fly barycentre correction of the psrtime file. Still does not look very good.
| VP0001 | VP0337 | VP0616 |
 |
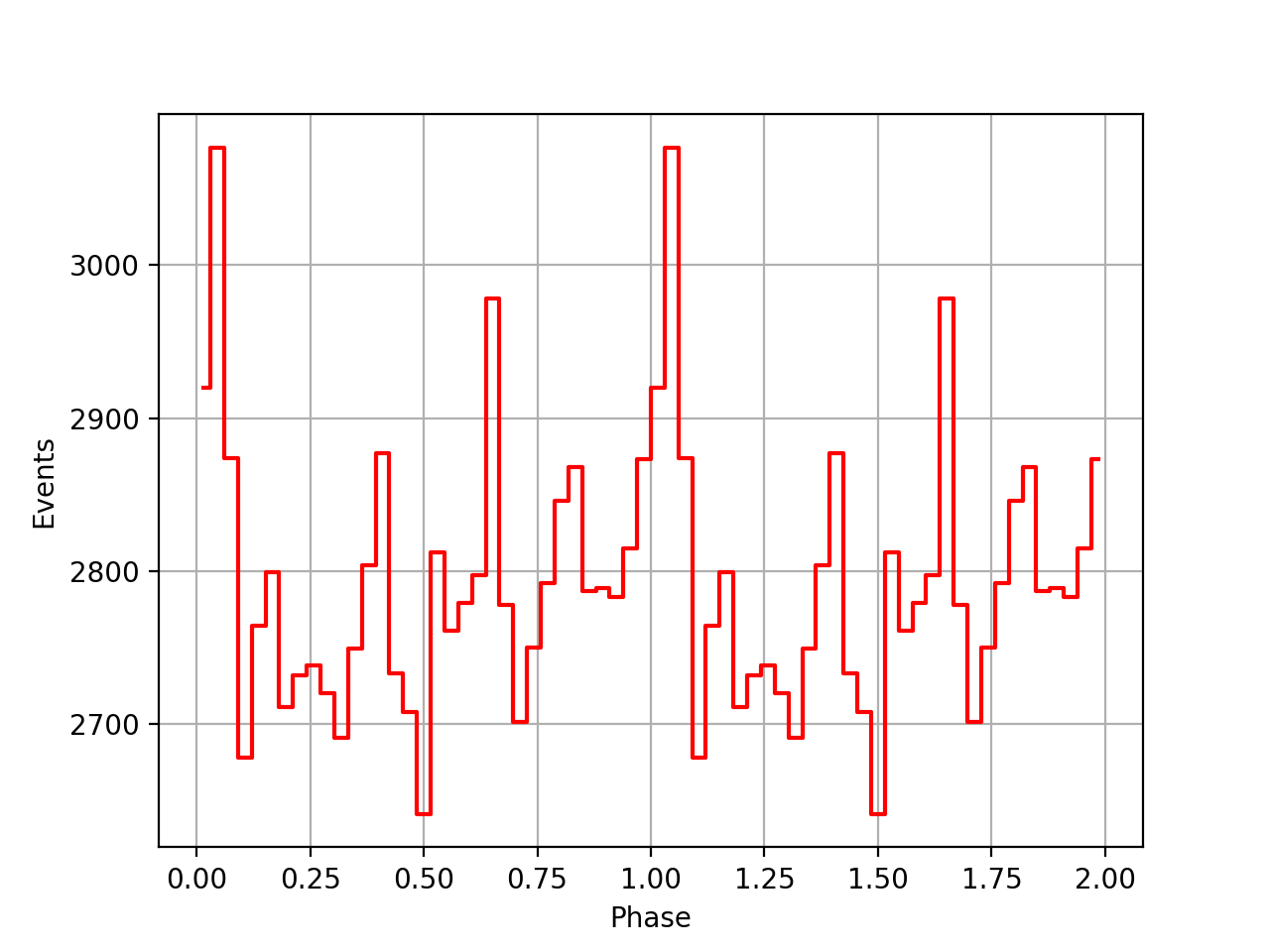 |
 |
#34
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
The question to answer now is in which time system the COMPTEL times are provided.
The evpbin02.pulbvc.f code takes on input UTC time of the event, which may suggest that COMPTEL times are in fact UTC times.
PULPHI COMPASS program:
- it computes the centre time of an observation using the
INTSTAandINTENDinformation in Julian Days and Modified Julian Days and hands this information over toPULA32to extrapolate the pulsar frequency, derivative and zero phase to the center of the epoch - it seems that in VP0032, which corresponds to 1992-06-25T01:00:00, a correction of 2.042144 s in the onboard time was applied. There exists in fact a
puliex02.timcor.Froutine that statesGRO Clock too fast by 2.042144 seconds (=16337.152 Tags). - the
pulbvc.ffunction is called withFTIME, which is the event time read from the EVP dataset. This implies that COMPTEL event times are in UTC.
The following time correction to the EVP data is employed:
IF ( ( FFTIME(1).LT.8798 ).OR.
1 ( (FFTIME(1).EQ.8798).AND.(FFTIME(2).LT.28800000)))THEN
FTIME(1) = FFTIME(1)
FTIME(2) = FFTIME(2) - ( 2.042144D0 * 8000.D0 )
IF ( FTIME(2) . LT. 0 )THEN
FTIME(1) = FTIME(1) - 1
FTIME(2) = FTIME(2) + ZZTIC
END IF
ELSE
FTIME(1) = FFTIME(1)
FTIME(2) = FFTIME(2)
END IF
This time correction needs to be implemented in the gammalib::com_time(), gammalib::com_tjd() and gammalib::com_tics() methods.
Note that I discovered that the methods did already consider that COMPTEL event times are given in UTC!
#35
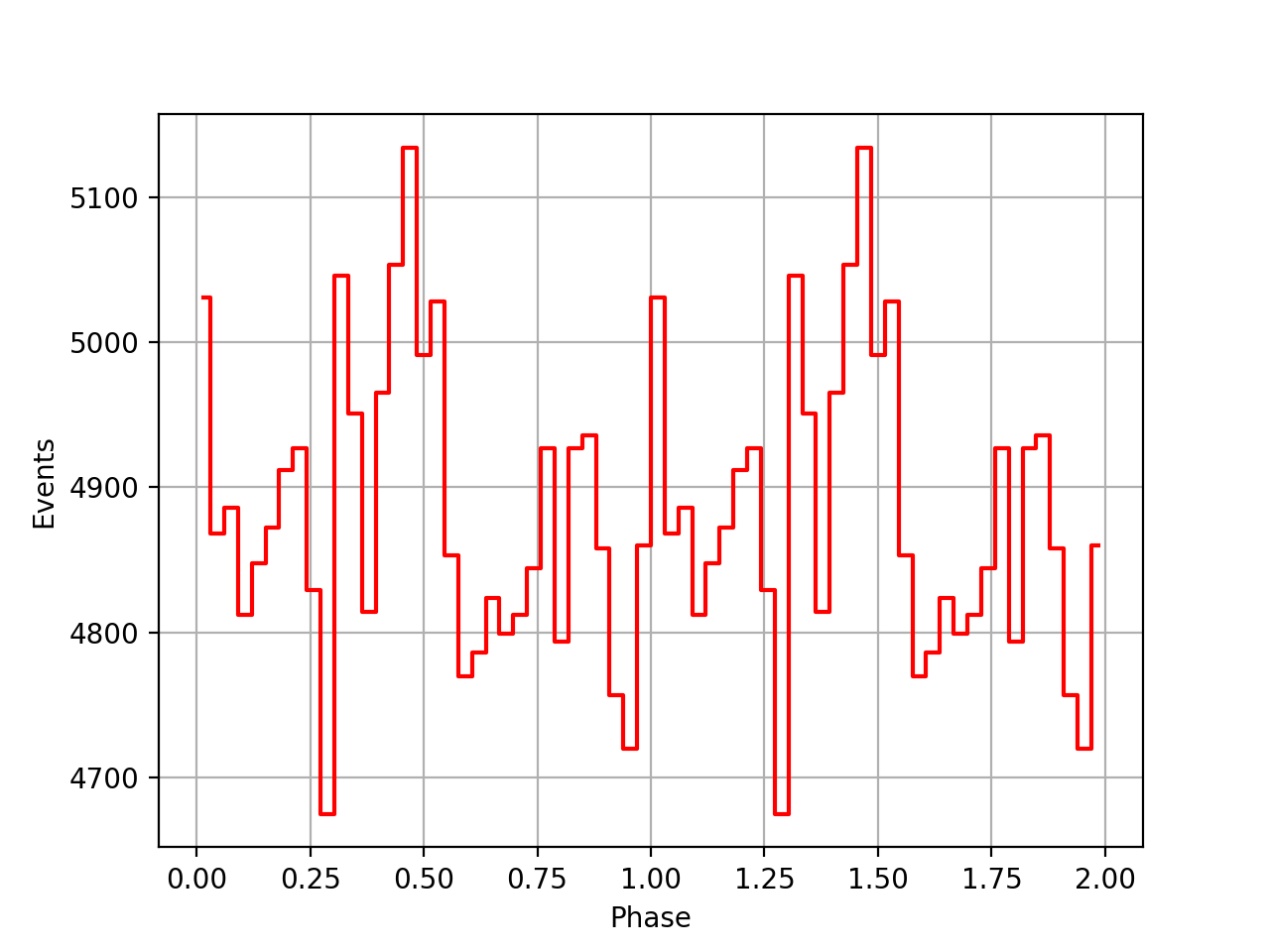
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
- File pulsar_vp0001_psrtime_20220114T1524.png added
- File pulsar_vp0337_psrtime_20220114T1524.png added
- File pulsar_vp0616_psrtime_20220114T1524.png added
Here the phase curves after implementing the clock correction and handling of the various time systems. Still does not look great.
| VP0001 | VP0337 | VP0616 |
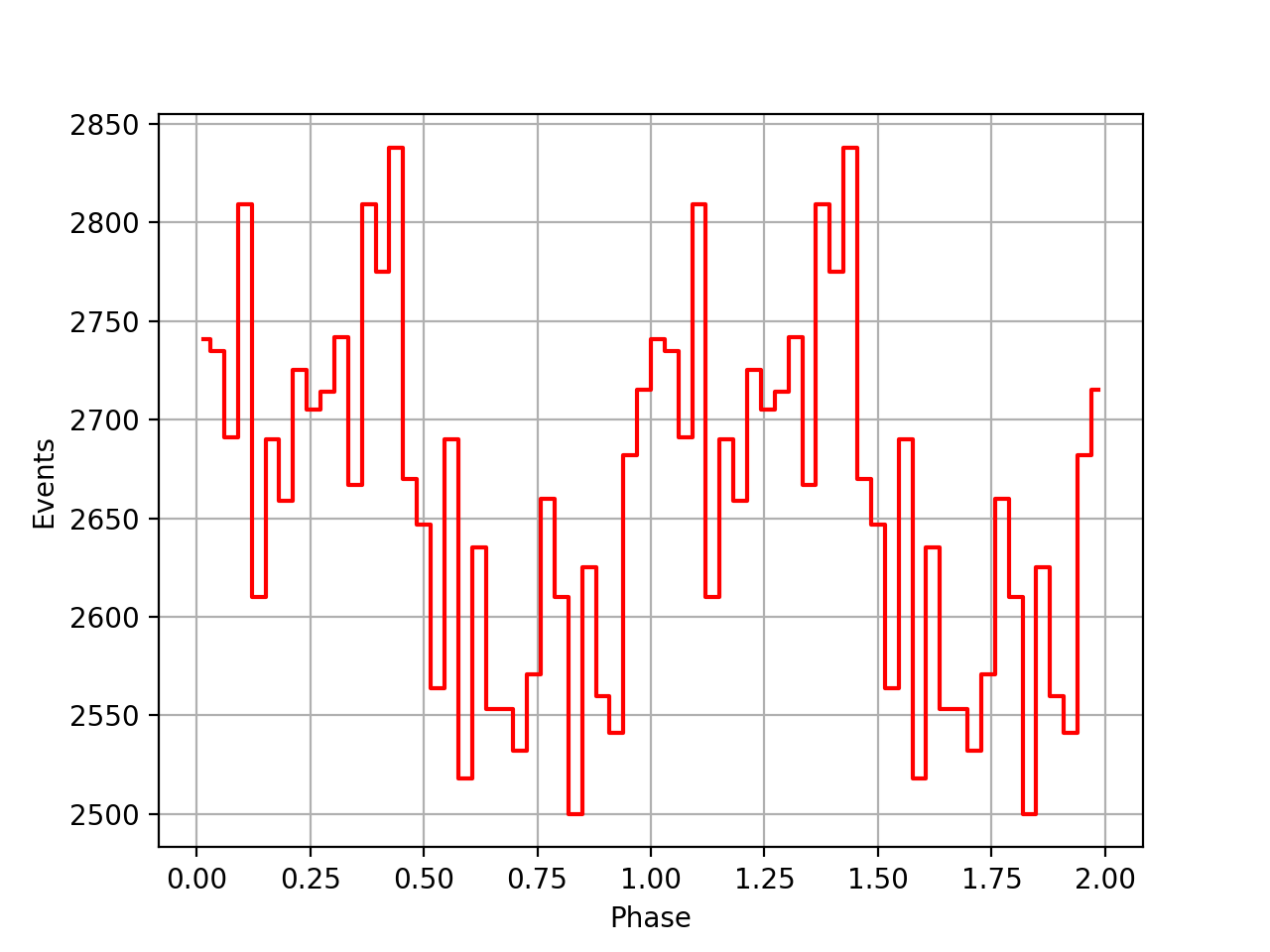 |
 |
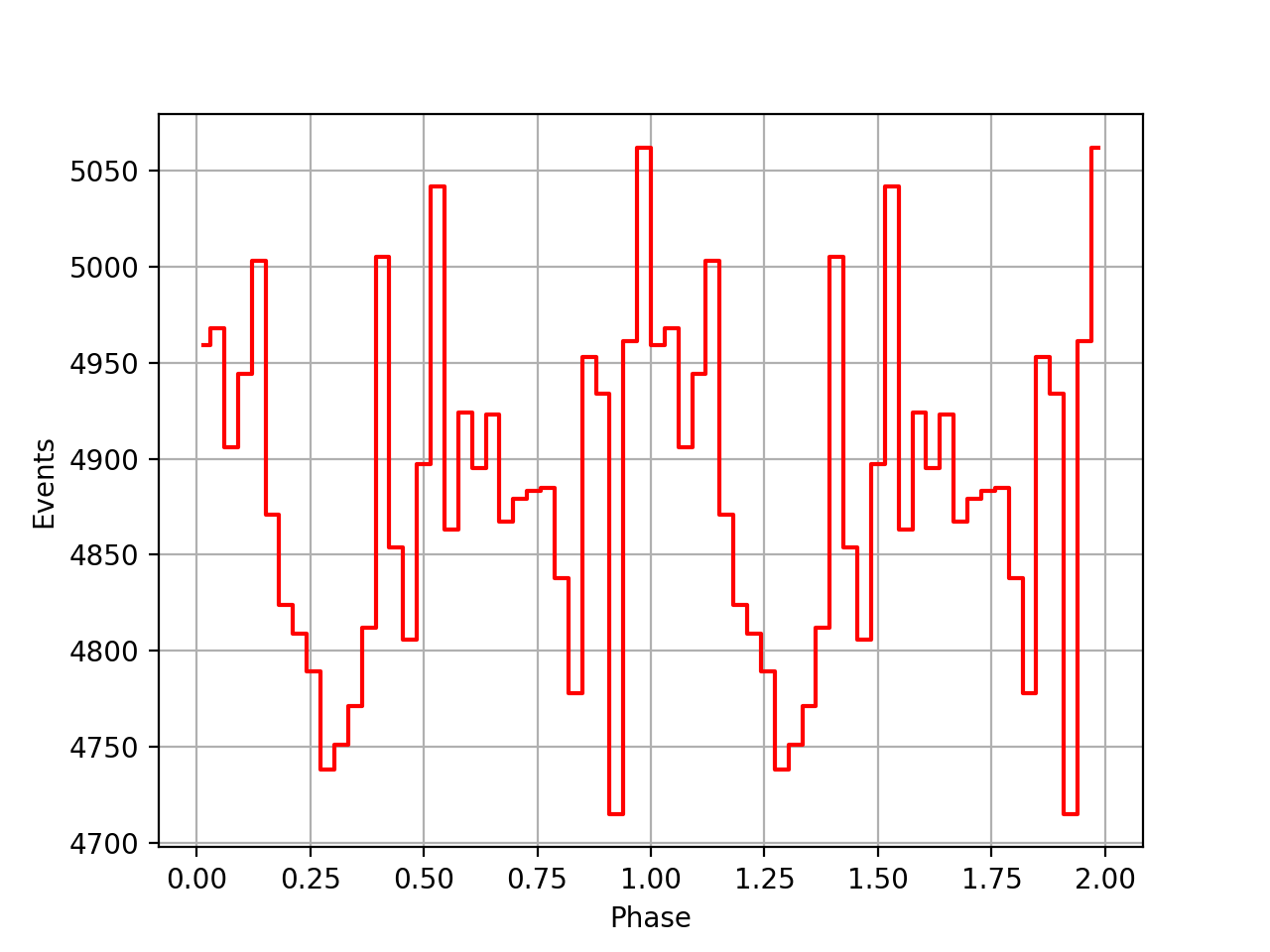 |
#36
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
- File pulsar_vp0001_psrtime_20220114T1538.png added
- File pulsar_vp0337_psrtime_20220114T1538.png added
- File pulsar_vp0616_psrtime_20220114T1538.png added
There was a bug in the TOA computation in GPulsar::load_psrtime. Maybe this looks a bit better, yet still the pulses do not seem to be aligned.
| VP0001 | VP0337 | VP0616 |
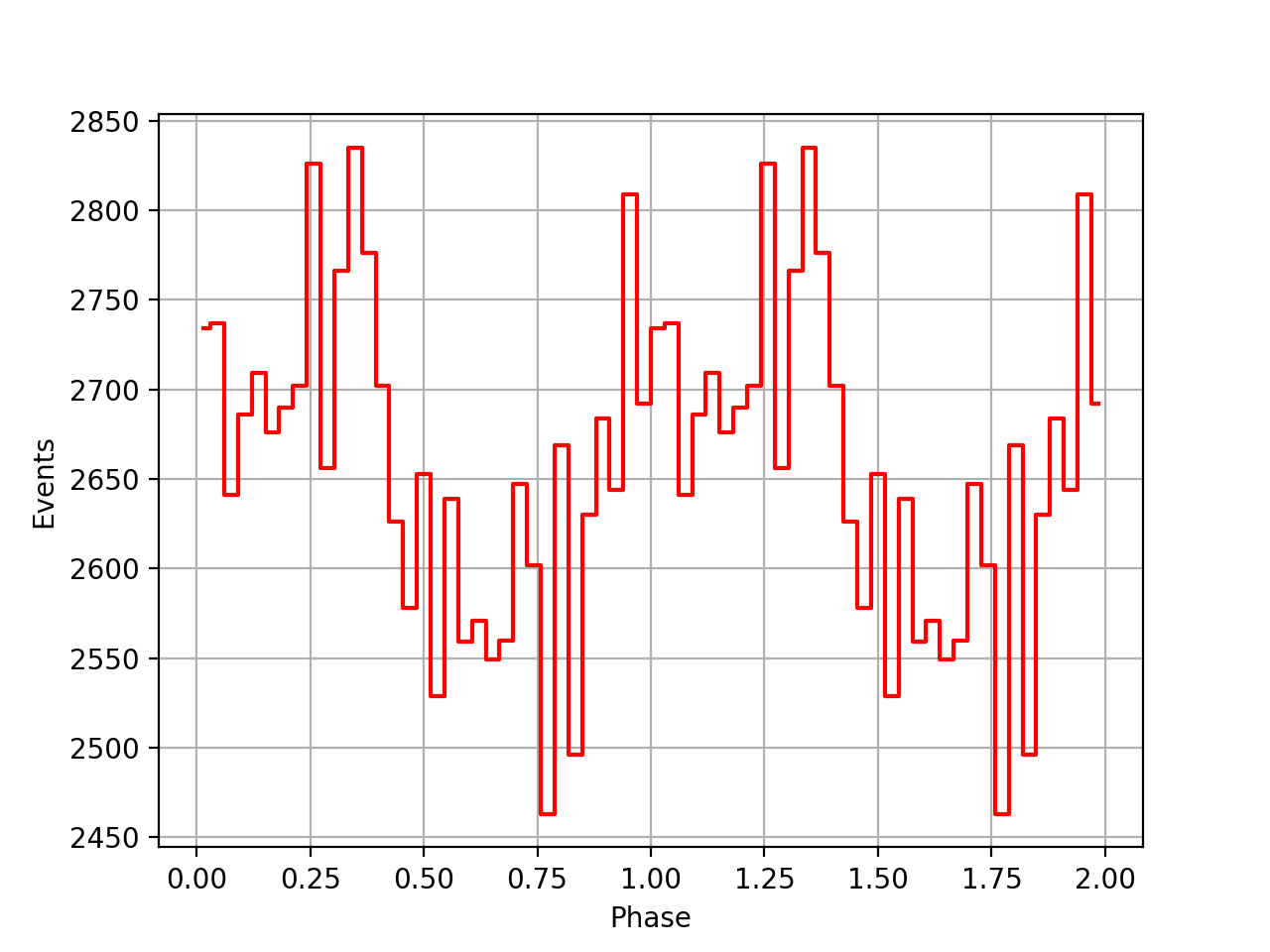 |
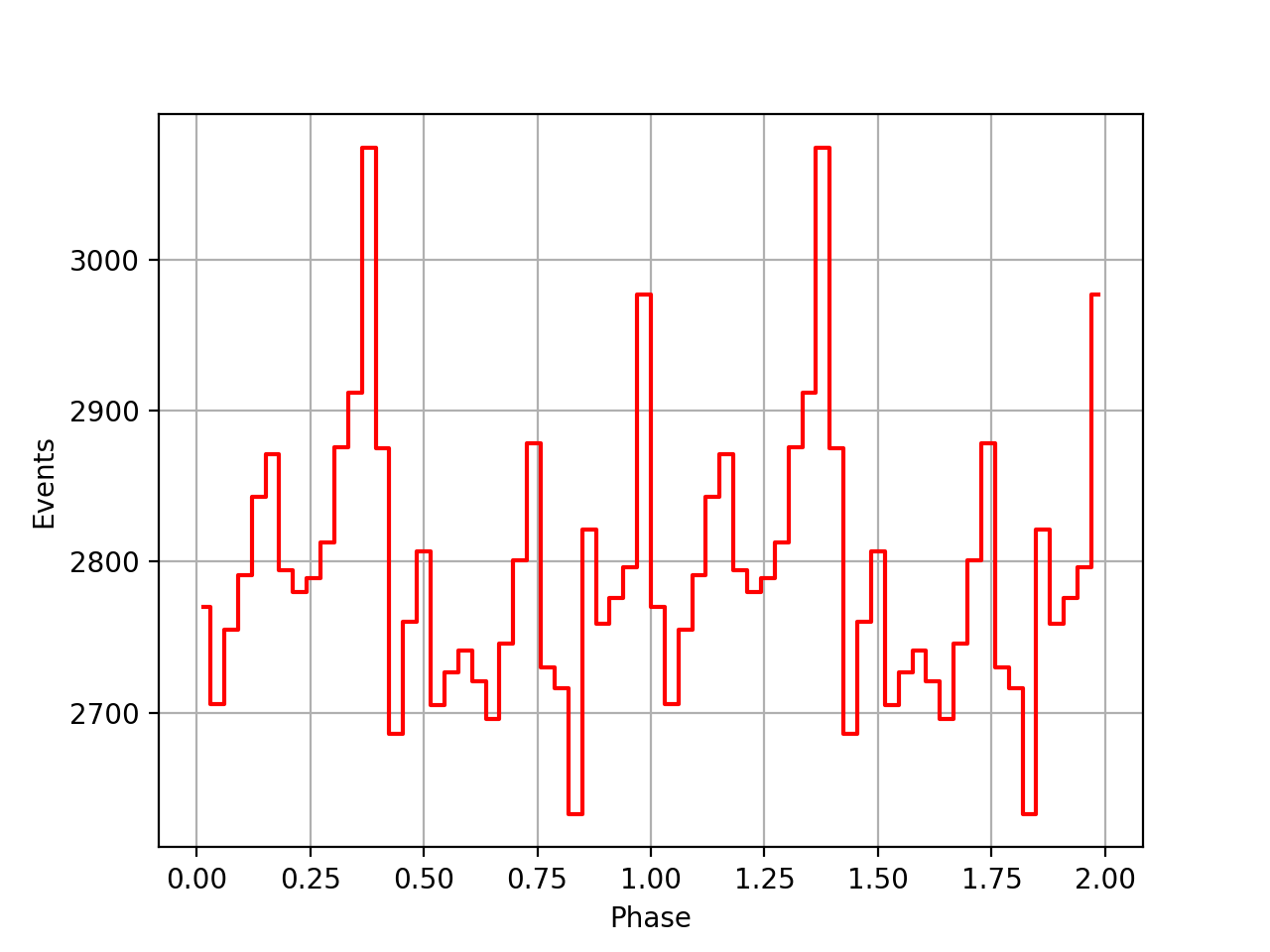 |
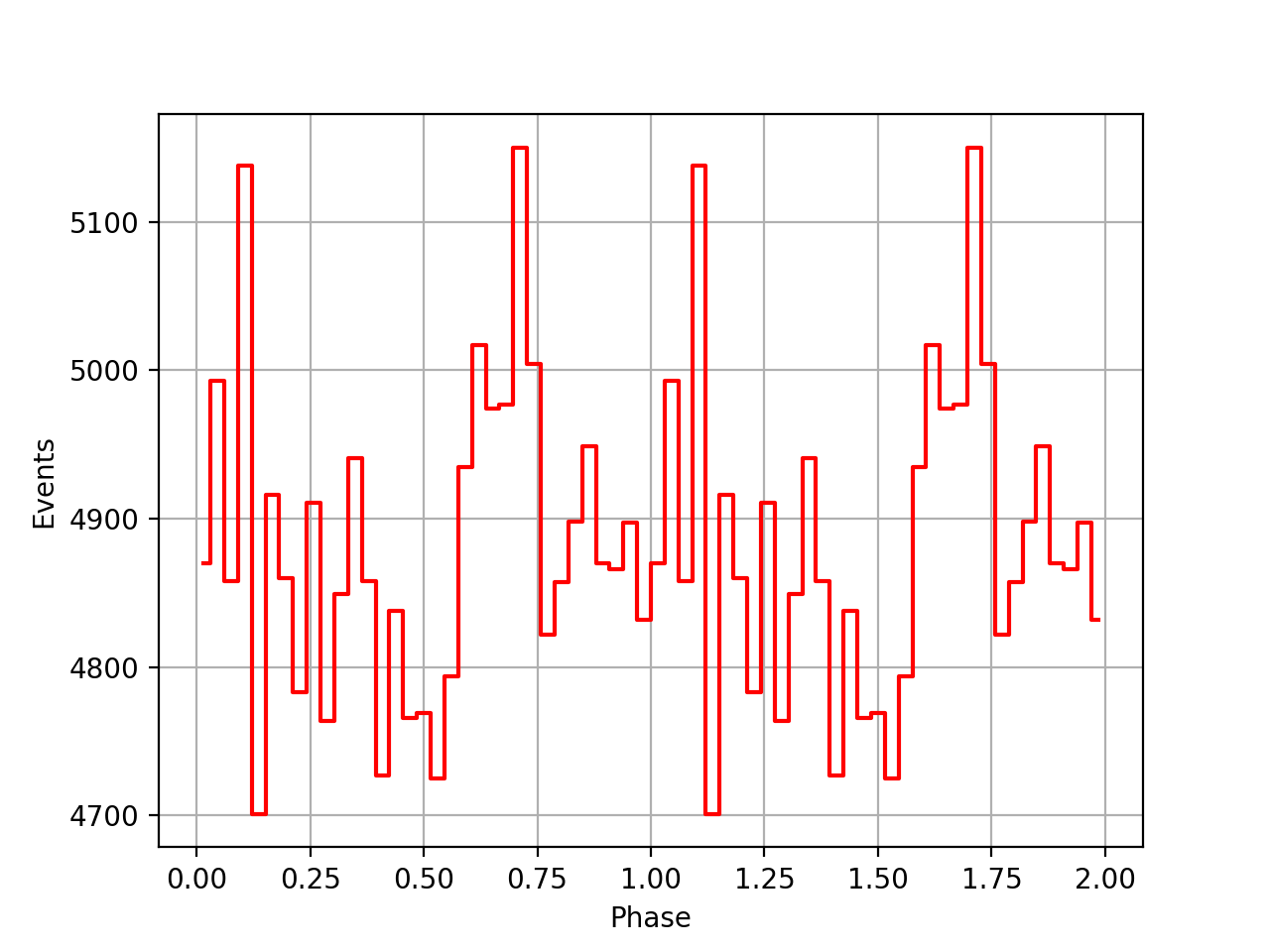 |
#37
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
- File pulsar_vp0001_psrtime_20220114T1606.png added
- File pulsar_vp0337_psrtime_20220114T1606.png added
- File pulsar_vp0616_psrtime_20220114T1606.png added
I implemented now the formula given in COM-RP-DOL-DRG-065 to compute the phase offset. The phasecurves I get somehow look similar to what I had earlier. I’m going round in circles.
| VP0001 | VP0337 | VP0616 |
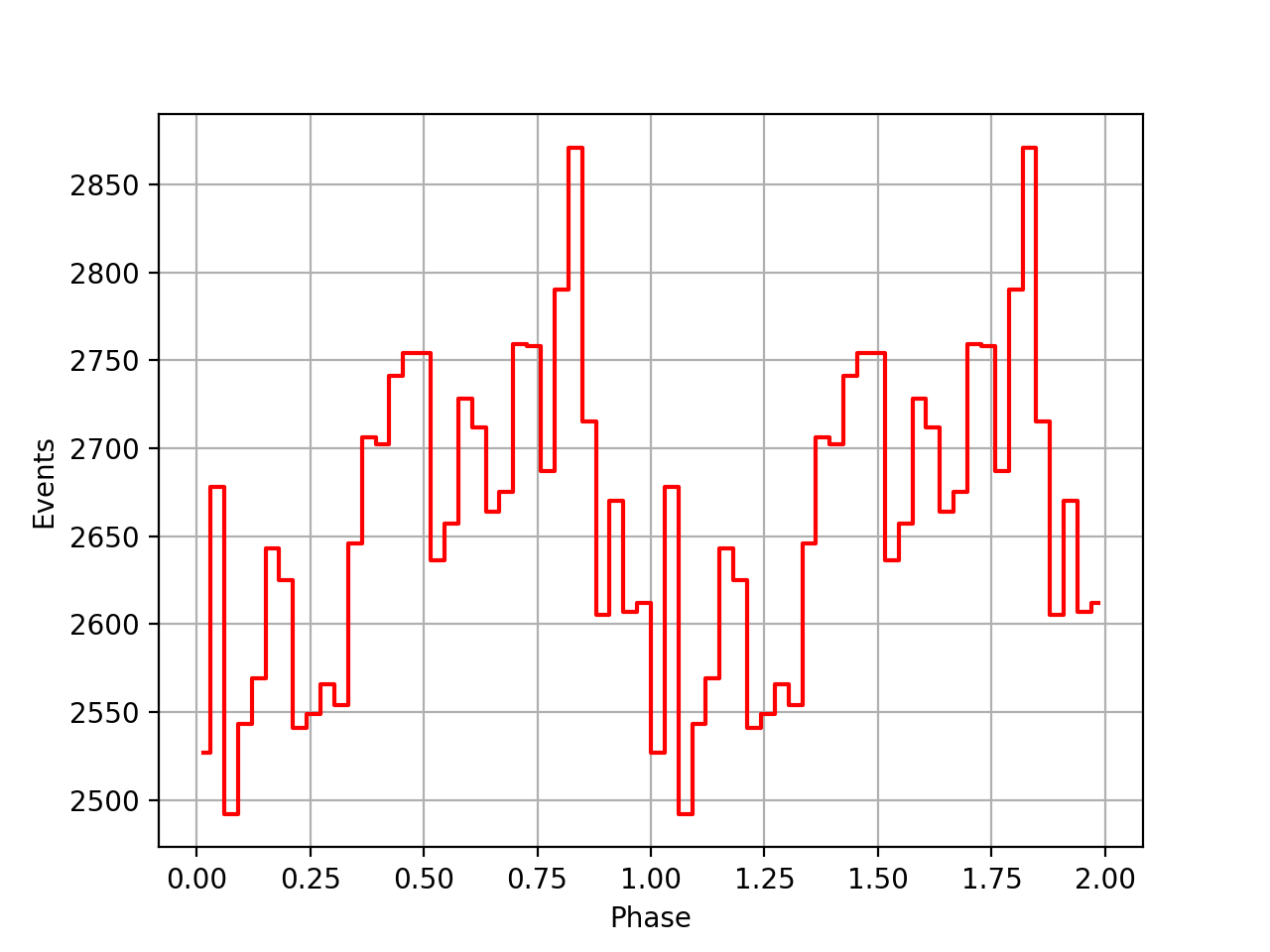 |
 |
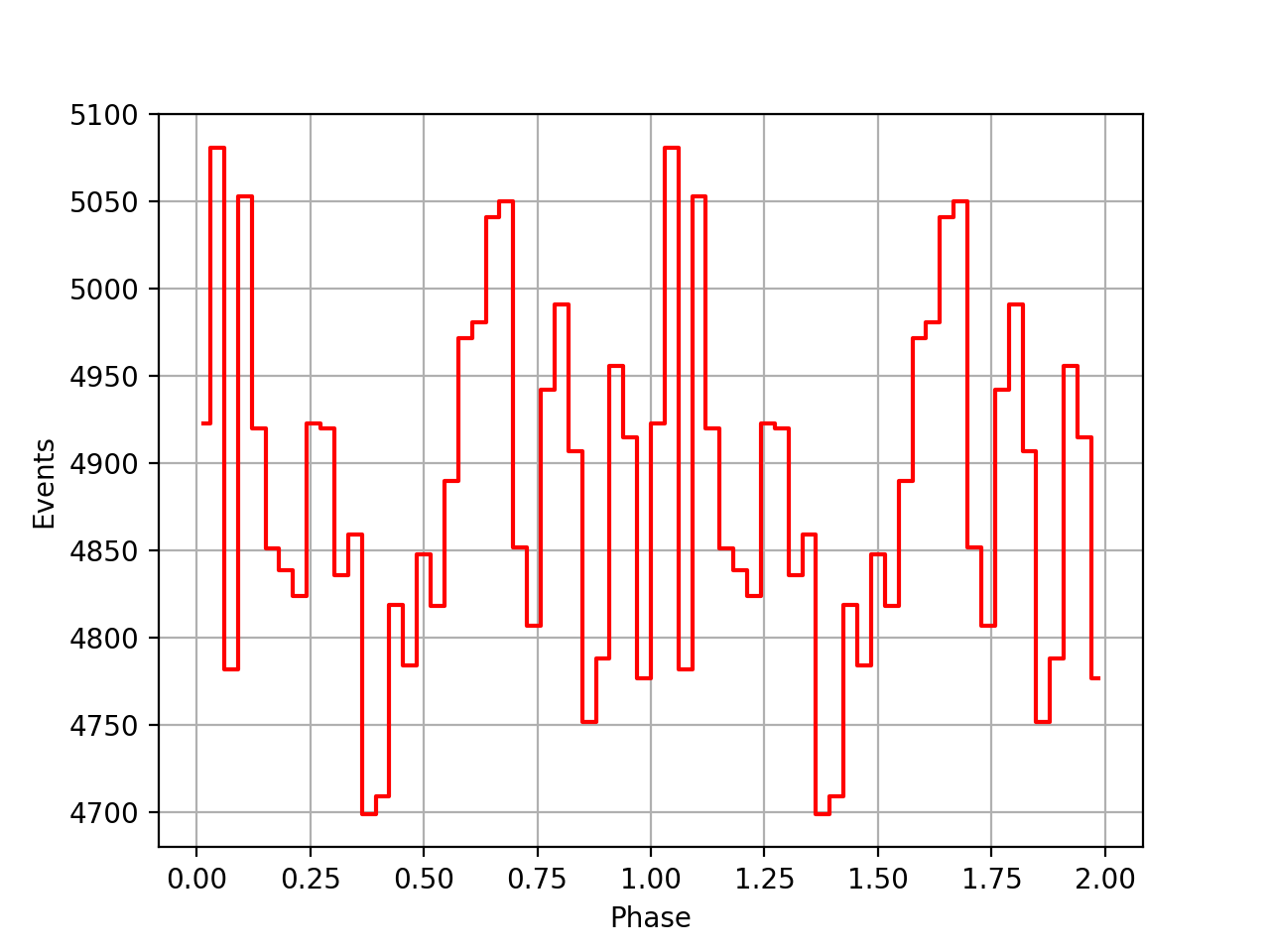 |
#38
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
Here is an selection of PPT datasets that were used at ROL for pulsar analysis in the COMPASS system. If I could get these datasets I may check the validity of the implementation:
R,PPT,98,Crab ephemeris : Obs. 213 from Princeton Catalogue,9047,0,9144,0,KUIPER,X,10/28/93 14:37,,,1,PULCCP,98,,,,,,, R,PPT,100,Crab ephemeris : Obs. 221 from Princeton Catalogue,9083,0,9173,0,KUIPER,X,10/29/93 16:16,,,1,PULCCP,100,,,,,,, R,PPT,136,Crab Princeton ephemeris 9296-9379 mid 9337,9296,0,9379,0,KUIPER,X,6/8/94 12:58,,,1,PULCP1,130,,,1,100,,11/27/95 10:13, R,PPT,138,Crab Princeton ephemeris 9340-9411 mid 9375 valid for Obs. 321.1+321.5,9340,0,9411,0,KUIPER,X,6/20/94 15:02,,,1,PULCP1,132,,,1,100,,11/27/95 10:13, R,PPT,141,Crab Princeton ephemeris 8331-8412 mid 8371 valid for Obs. 1,8331,0,8412,0,KUIPER,X,8/1/94 10:54,,,1,PULCP1,135,,,1,,,11/27/95 10:13, R,PPT,146,"Crab (PSR B0531+21) 9047-9144 mid 9095 valid for Obs. 213 , 221",9047,0,9144,0,KUIPER,X,8/9/94 10:45,,,1,PULCP1,140,,,1,100,,11/27/95 10:13, R,PPT,155,"Crab (PSR B0531+21) 8331-8412 mid 8371 valid for Obs. 0.3,0.4,0.5,1.0",8331,0,8412,0,KUIPER,X,9/8/94 12:36,,,1,PULCP1,149,,,1,100,,11/27/95 10:13, R,PPT,157,Crab Princeton ephemeris 8406-8493 mid 8449 valid for Obs. 2.5,8406,0,8493,0,KUIPER,X,9/20/94 13:16,,,1,PULCP1,151,,,1,100,,11/27/95 10:13, R,PPT,158,Crab Princeton ephemeris 8499-8637 mid 8568 valid for Obs. 15,8499,0,8637,0,KUIPER,X,9/20/94 13:18,,,1,PULCP1,152,,,1,100,,11/27/95 10:13, R,PPT,159,Crab Princeton ephemeris 8637-8801 mid 8719 valid for Obs. 31,8637,0,8801,0,KUIPER,X,9/20/94 13:23,,,1,PULCP1,153,,,1,100,,11/27/95 10:13, R,PPT,160,"Crab Princeton ephemeris 8801-8913 mid 8857 valid for Obs. 36.0,36.5,39,41",8801,0,8913,0,KUIPER,X,9/20/94 13:26,,,1,PULCP1,154,,,1,100,,11/27/95 10:13, R,PPT,161,"Crab Princeton ephemeris 8884-8943 mid 8913 valid for Obs. 41,44",8884,0,8943,0,KUIPER,X,9/20/94 13:30,,,1,PULCP1,155,,,1,100,,11/27/95 10:13, R,PPT,164,Crab ephemeris for VP 337 with MJD 49598,9526,0,9671,0,KUIPER,X,11/23/94 16:37,,,1,PULCP1,158,,,1,100,,11/27/95 10:13, R,PPT,193,Crab VP 337 49598,9526,0,9671,0,KUIPER,X,2/7/95 16:58,,,1,PULCP2,28,1,258662,1,200,,11/27/95 10:13, R,PPT,204,Crab VP 0.2+0.3+0.4+0.5+1 Center 8371,8331,0,8412,0,KUIPER,X,5/23/95 14:42,,,1,PULCP2,39,1,274360,1,200,,11/27/95 10:13, R,PPT,219,PSR 0531+21 (Crab) VP 412.0+413.0 Center 9780,9751,0,9810,0,KUIPER,X,8/3/95 16:11,,,1,PULCP2,54,1,285935,1,200,,11/27/95 10:13, R,PPT,230,PSR 0531+21 (Crab) VP 419.1+419.5+420 Center 9842,9791,0,9893,0,KUIPER,X,11/1/95 15:17,,,1,PULCP2,65,1,302171,1,200,,11/27/95 10:13,R,PPT,235,PSR 0531+21 (Crab) VP 426.0+427 Center 9961,9931,0,9992,0,KUIPER,X,11/2/95 15:39,,,1,PULCP2,70,1,302415,1,200,,11/27/95 10:13, R,PPT,238,PSR 0531+21 (Crab) VP 2.5 Center 8449,8406,0,8493,0,KUIPER,X,11/21/95 11:18,,,1,PULCP2,73,1,304244,1,200,,11/27/95 10:13, R,PPT,239,PSR 0531+21 (Crab) VP 15 Center 8568,8499,0,8637,0,KUIPER,X,11/21/95 11:29,,,1,PULCP2,74,1,304247,1,200,,11/27/95 10:13, R,PPT,240,PSR 0531+21 (Crab) VP 31 Center 8719,8637,0,8801,0,KUIPER,X,11/21/95 11:33,,,1,PULCP2,75,1,304250,1,200,,11/27/95 10:13, R,PPT,241,PSR 0531+21 (Crab) VP 36.0+36.5+39+41 Center 8857,8801,0,8913,0,KUIPER,X,11/21/95 11:39,,,1,PULCP2,76,1,304253,1,200,,11/27/95 10:13, R,PPT,242,PSR 0531+21 (Crab) VP 41+44 Center 8913,8884,0,8943,0,KUIPER,X,11/21/95 11:46,,,1,PULCP2,77,1,304256,1,200,,11/27/95 10:13, R,PPT,243,PSR 0531+21 (Crab) VP 310 Center 9337,9296,0,9379,0,KUIPER,X,11/21/95 12:06,,,1,PULCP2,78,1,304259,1,200,,11/27/95 10:13, R,PPT,244,PSR 0531+21 (Crab) VP 321.1+321.5 Center 9375,9340,0,9411,0,KUIPER,X,11/21/95 12:09,,,1,PULCP2,79,1,304262,1,200,,11/27/95 10:13, R,PPT,248,PSR 0531+21 (Crab) VP 502 Center 10009,9991,0,10028,0,KUIPER,X,1/10/96 11:51,,,1,PULCP2,83,1,307331,1,,,, R,PPT,273,PSR 0531+21 (Crab) VP 502 Center 10009,9991,0,10028,0,KUIPER,X,3/28/96 11:22,,,1,PULCP2,108,1,317884,1,,,, R,PPT,274,PSR 0531+21 (Crab) VP 502 Center 10009,9991,0,10028,0,KUIPER,X,3/28/96 11:25,,,1,PULCP2,109,1,317890,1,,,, R,PPT,292,PSR B0531+21 (Crab) 10204 10235 VP 520 (Correction for Feb 1996),10204,0,10235,0,KUIPER,X,7/18/96 15:54,,,1,PULCP3,17,2,327558,1,,,, R,PPT,294,PSR B0531+21 (Crab) 10084 10098 VP 510.0/510.5,10084,0,10155,0,KUIPER,X,7/19/96 15:59,,,1,PULCP3,19,2,327696,1,,,, R,PPT,296,PSR B0531+21 (Crab) 10204 10235 VP 520,10204,0,10235,0,KUIPER,X,8/2/96 10:02,,,1,PULCP3,21,2,328248,1,,,, R,PPT,300,PSR B0531+21 (Crab) 10142 10259 VP 520,10142,0,10259,0,KUIPER,X,11/4/96 14:57,,,1,PULCP3,25,2,334202,1,,,, R,PPT,302,PSR B0531+21 (Crab) 10260 10292 VP 523 Crab DEC2000 Modified,10260,0,10292,0,KUIPER,X,11/5/96 17:41,,,1,PULCP3,27,2,334268,1,,,, R,PPT,305,PSR B0531+21 (Crab) 10267-10310 VP 526 Crab DEC2000 Modified,10267,0,10310,0,KUIPER,X,11/25/96 15:32,,,1,PULCP3,30,2,335891,1,,,, R,PPT,307,PSR B0531+21 (Crab) 10267-10310 VP 526 Crab new entry,10267,0,10310,0,KUIPER,X,12/9/96 11:31,,,1,PULCP3,32,2,337438,1,,,, R,PPT,309,PSR B0531+21 (Crab) 10260 10292 VP 523 Crab,10260,0,10292,0,KUIPER,X,12/9/96 11:50,,,1,PULCP3,34,2,337450,1,,,, R,PPT,311,PSR B0531+21 (Crab) 10297-10325 VP 527/528 (VP 526 Partly) New entry,10297,0,10325,0,KUIPER,X,12/10/96 14:45,,,1,PULCP3,36,2,337792,1,,,, R,PPT,330,PSR B0531+21 (Crab) 10491-10539 VP 616.1,10491,0,10539,0,KUIPER,X,7/25/97 15:01,,,1,PULCP3,55,2,355079,1,,,, R,PPT,365,PSR B0531+21 9400- 9551 / mid 9475 Princeton VP 325,9400,0,9551,0,KUIPER,X,1/5/99 19:47,,,1,PULCP3,90,2,408590,1,,,, R,PPT,367,PSR B0531+21 10311-10409 / mid 10360 Princeton VP 520.9,10311,0,10409,0,KUIPER,X,1/6/99 11:59,,,1,PULCP3,92,2,408695,1,,,, R,PPT,369,"PSR B0531+21 10530-10575 / mid 10552 Princeton VP (617.1),617.3,617.5,617.7",10530,0,10575,0,KUIPER,X,1/6/99 18:26,,,1,PULCP3,94,2,408743,1,,,, R,PPT,371,PSR B0531+21 10630-10660 / mid 10645 Princeton VP 623 Partly,10630,0,10660,0,KUIPER,X,1/8/99 15:12,,,1,PULCP3,96,2,408869,1,,,, R,PPT,372,PSR B0531+21 10655-10685 / mid 10670 Princeton VP 623 Partly,10655,0,10685,0,KUIPER,X,1/8/99 15:14,,,1,PULCP3,97,2,408872,1,,,, R,PPT,388,PSR B0531+21 10957-11057 / mid 11007 Princeton VP 724.5,10957,0,11057,0,KUIPER,X,1/18/99 13:50,,,1,,,,,1,100,,1/18/99 15:31, R,PPT,401,PSR B0531+21 11299-11330 / mid 11314 Jodrell Bank VP 815/816,11299,0,11330,0,KUIPER,X,3/21/00 16:16,,,1,PULCP3,126,2,437131,1,,,, R,PPT,402,PSR B0531+21 11422-11451 / mid 11436 Jodrell Bank VP 829,11422,0,11451,0,KUIPER,X,3/21/00 16:16,,,1,PULCP3,127,2,437134,1,,,, R,PPT,403,PSR B0531+21 11513-11543 / mid 11528 Jodrell Bank VP 903.1,11513,0,11543,0,KUIPER,X,3/21/00 16:17,,,1,PULCP3,128,2,437137,1,,,, R,PPT,407,PSR B0531+21 11635-11665 / mid 11650 Jodrell Bank VP 918.5,11635,0,11665,0,KUIPER,X,11/6/00 17:37,,,1,PULCP3,132,2,439030,1,,,, R,PPT,408,PSR B0531+21 11665-11696 / mid 11680 Jodrell Bank VP 918.5,11665,0,11696,0,KUIPER,X,11/6/00 17:37,,,1,PULCP3,133,2,439033,1,,,, R,PPT,426,PSR B0531+21 11575-11604 / mid 11590 Jodrell Bank February 2000 Chandra Crab,11575,0,11604,0,KUIPER,X,3/28/01 13:31,,,1,PULCP3,151,2,443930,1,,,,
#39
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
- File pulphi.py
 added
added - File pulsar_vp0001_0337_0616_psrtime_20220118T1626.png added
- File pulsar_vp0001_psrtime_20220118T1626.png added
- File pulsar_vp0337_psrtime_20220118T1626.png added
- File pulsar_vp0616_psrtime_20220118T1626.png added
- % Done changed from 60 to 70
I reimplemented the COMPASS tasks pulcpp and pulphi to compare the COMPASS computations to the computation done in compulbin and the relevant GammaLib classes and methods. The code is here: pulphi.py.
Here is a comparison of the pulphi computations to compulbin. The computations are done for the psrtime ephemeris for VP0001 (line 53 of the psrtime file). There was a bug in the GammaLib code that used the Sun vector instead of the Earth vector for the Barycentric corrections of the pulsar ephemeris. Once corrected the overall agreement of the results is quite good.
| Parameter | pulphi |
compulbin |
| Frequency | 29.948566 | 29.9485663 |
| Frequency derivative | -3.776410e-10 | -3.77641e-10 |
| Second freq. derivative | 0.000000e+00 | 0 |
| Pos1 | 0.102809 | 0.102807511008044 |
| Pos2 | 0.921371 | 0.921371319681263 |
| Pos3 | 0.374841 | 0.374840642072253 |
| Rce_x | -290.18898269210274 | -290.188982692728 |
| Rce_y | -377.46818014285276 | -377.468180142437 |
| Rce_z | -163.70086667365896 | -163.700866673479 |
| dt (sec) | -0.499326350076 | -0.49932635 |
| UTC → TDT (sec) | 58.184000 | 58.184 |
| TDT → TDB (sec) | 0.001234 | 0.00123448826 |
| UTC → TDB (sec) | 58.185234 | 58.1852344883 |
| Traveltime difference (sec) | -438.984165 | -438.9837003 |
| Relativistic delay (sec) | 0.000020 | 2.02210726e-05 |
| Total delay (sec) | -380.798951 | -380.798486 |
| Time difference to nominal epoch (sec) | -380.779597 | -380.779133 |
| Radio-phase 0 at nominal epoch | 0.196941 | 0.210863081 |
| Pulsar epoch JD | 2448392.500000 | 2448392.5 |
| Pulsar epoch MJD | 48392.000000 | 48392.0007 |
| Radio phase | -0.196941 | -0.210863081 |
Below a phase computation comparison for 3 events. The first line corresponds to the pulphi results, the second line to the compulbin results. Also here the agreement is quite good.
| Event | Event time (UTC) | Event time (clock corrected) | Event time (SSB) | Time difference | Phase |
| 14 | 8392:624148236 | 8392:624131898 | 8392:621055220 | -384.58487032 | 0.84946251 |
| 14 | 8392:624148236 | 8392:624131899 | 8392:621071560 | -384.58446354 | 0.84412106 |
| 34 | 8392:624498322 | 8392:624481984 | 8392:621405298 | -384.58584732 | 0.38995552 |
| 34 | 8392:624498322 | 8392:624481985 | 8392:621421638 | -384.58544035 | 0.38529532 |
| 70 | 8392:624964936 | 8392:624948598 | 8392:621871902 | -384.58714836 | 0.15334892 |
| 70 | 8392:624964936 | 8392:624948599 | 8392:621888242 | -384.58674152 | 0.14715434 |
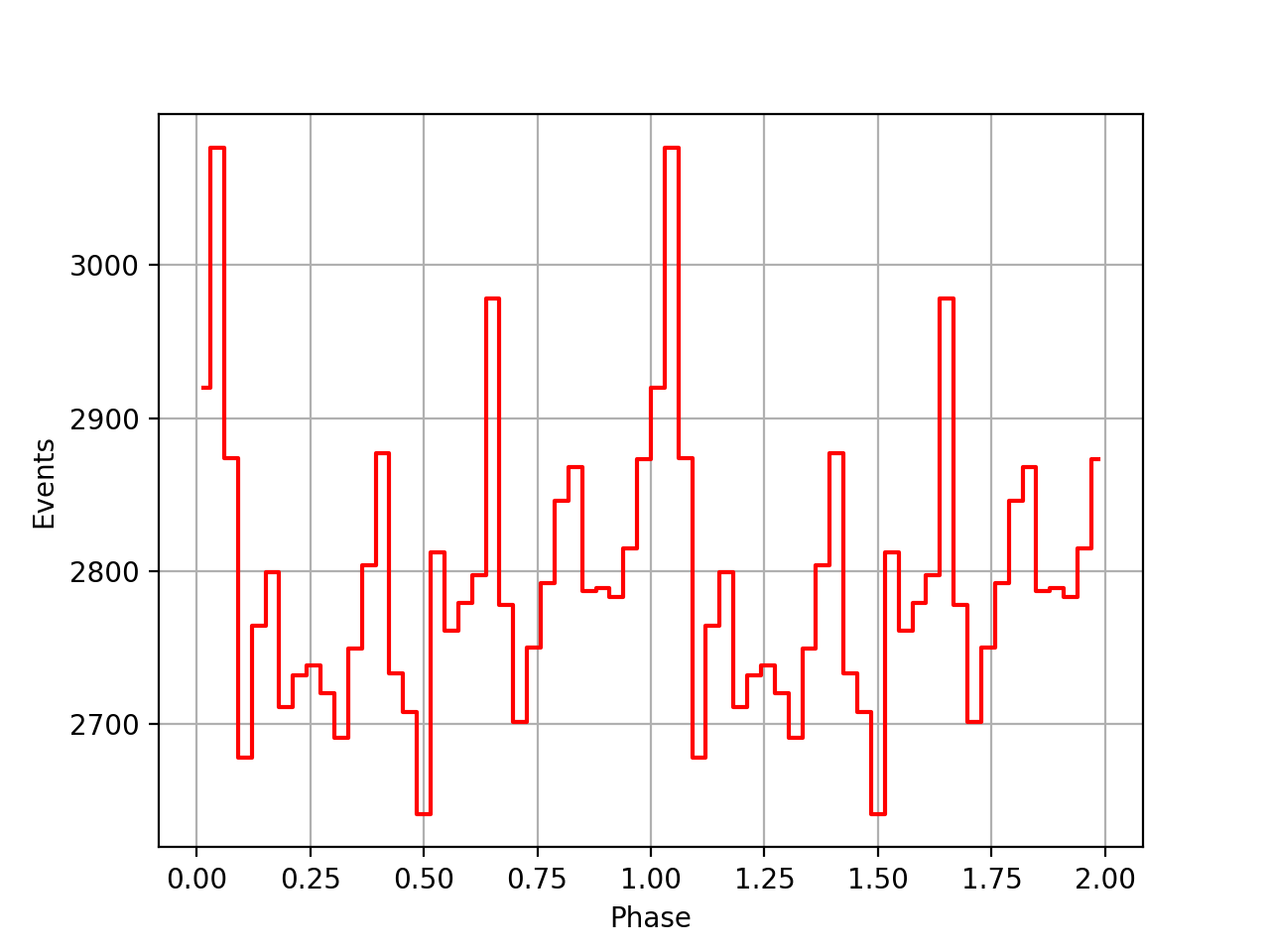
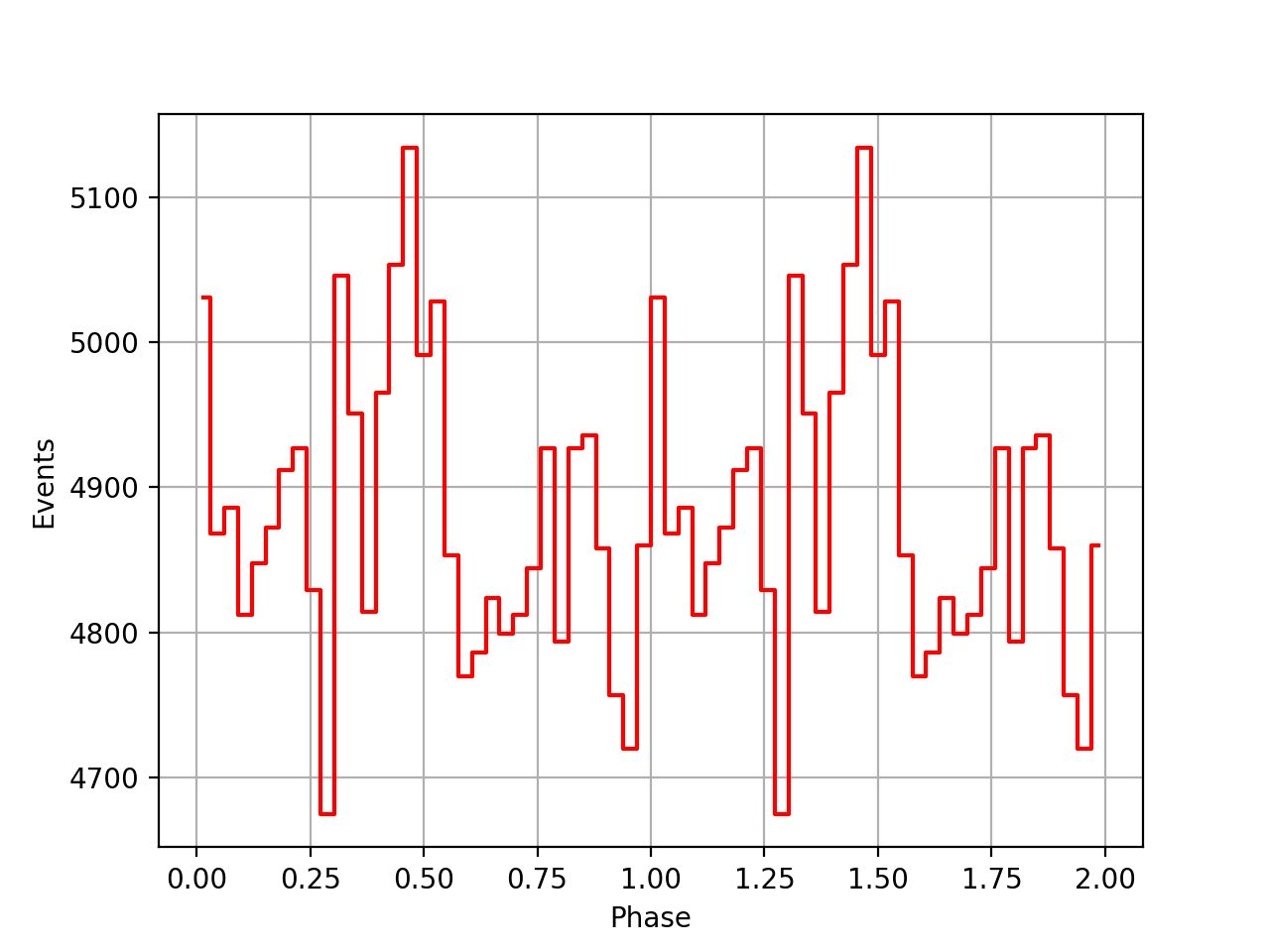
Finally the phase curves for the 3 VPs, and all 3 VPs combined. There is still a misalignment between the VPs, maybe due to an additional phase shift that is not in the ephemeris. For VP0337 and VP0616 the phase curves seem to be aligned.
| VP0001 | VP0337 | VP0616 | All |
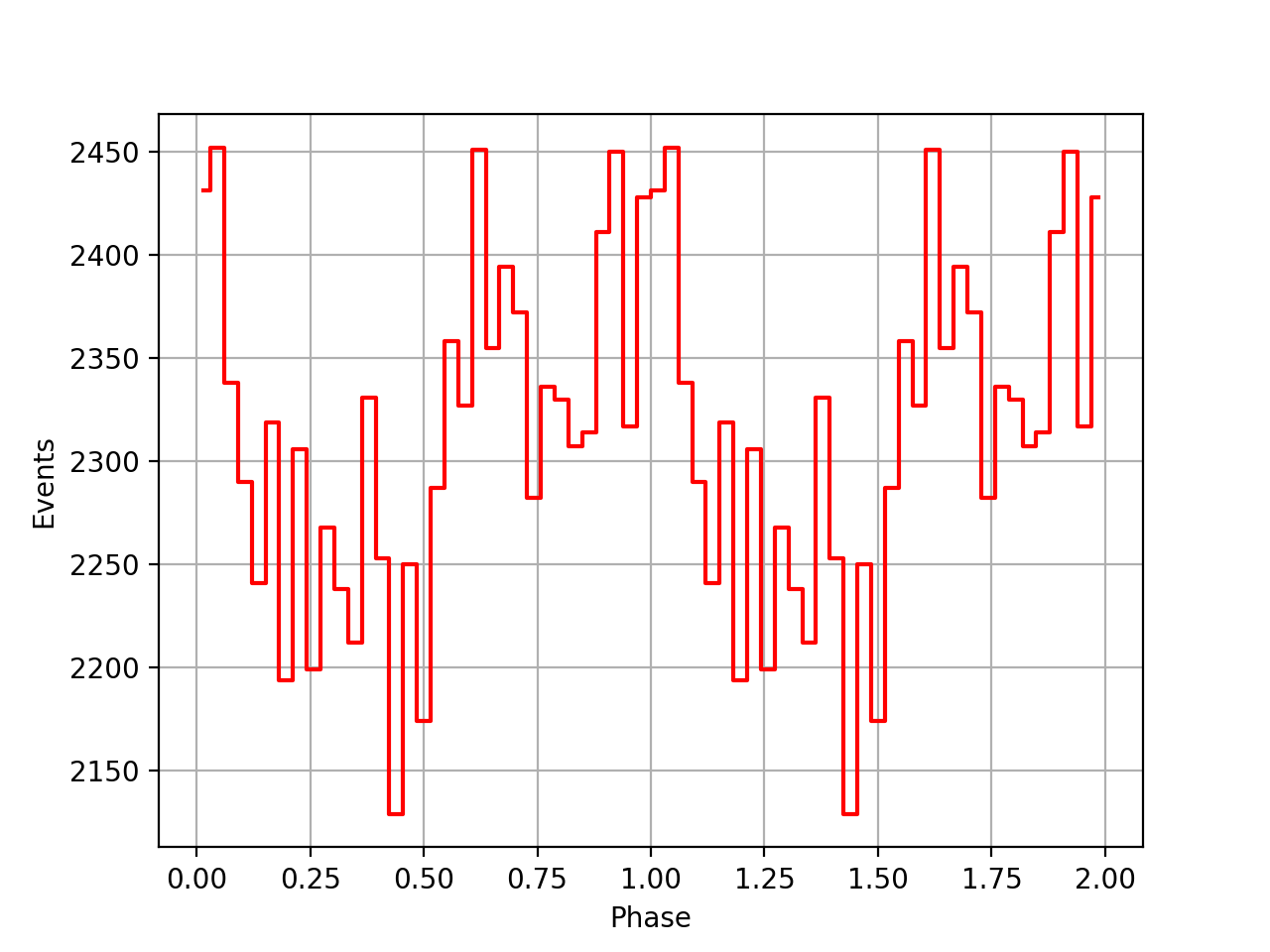 |
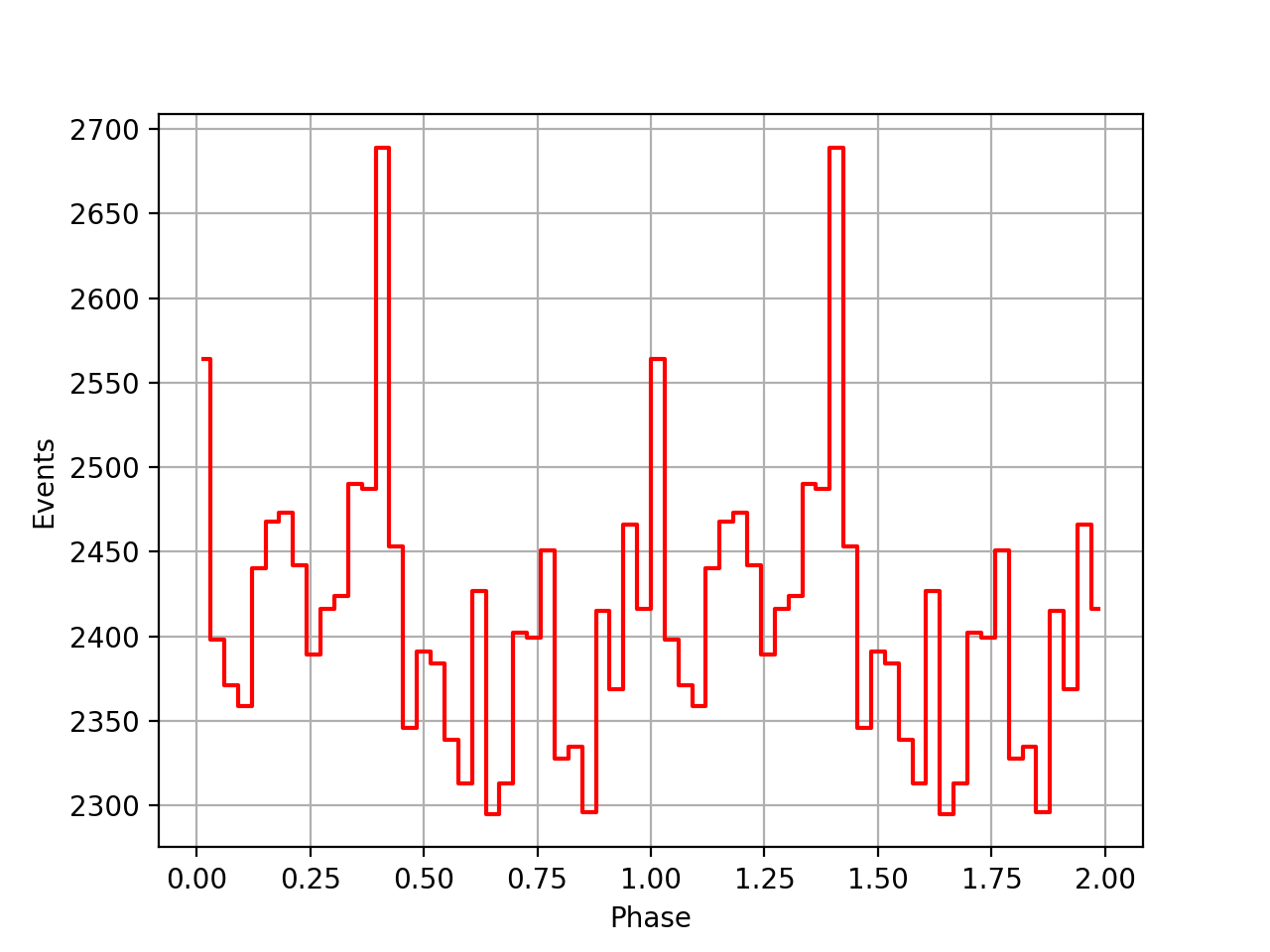 |
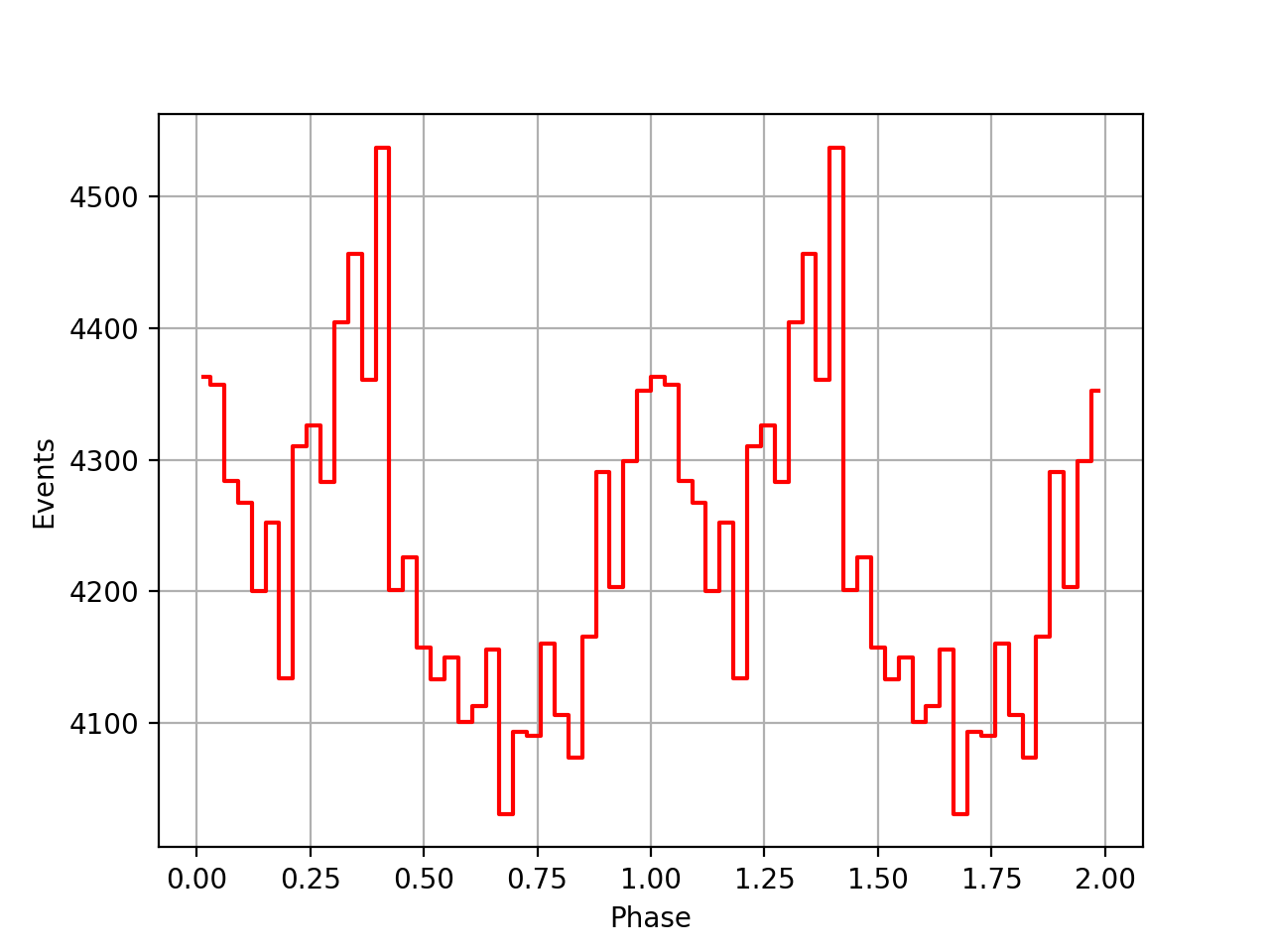 |
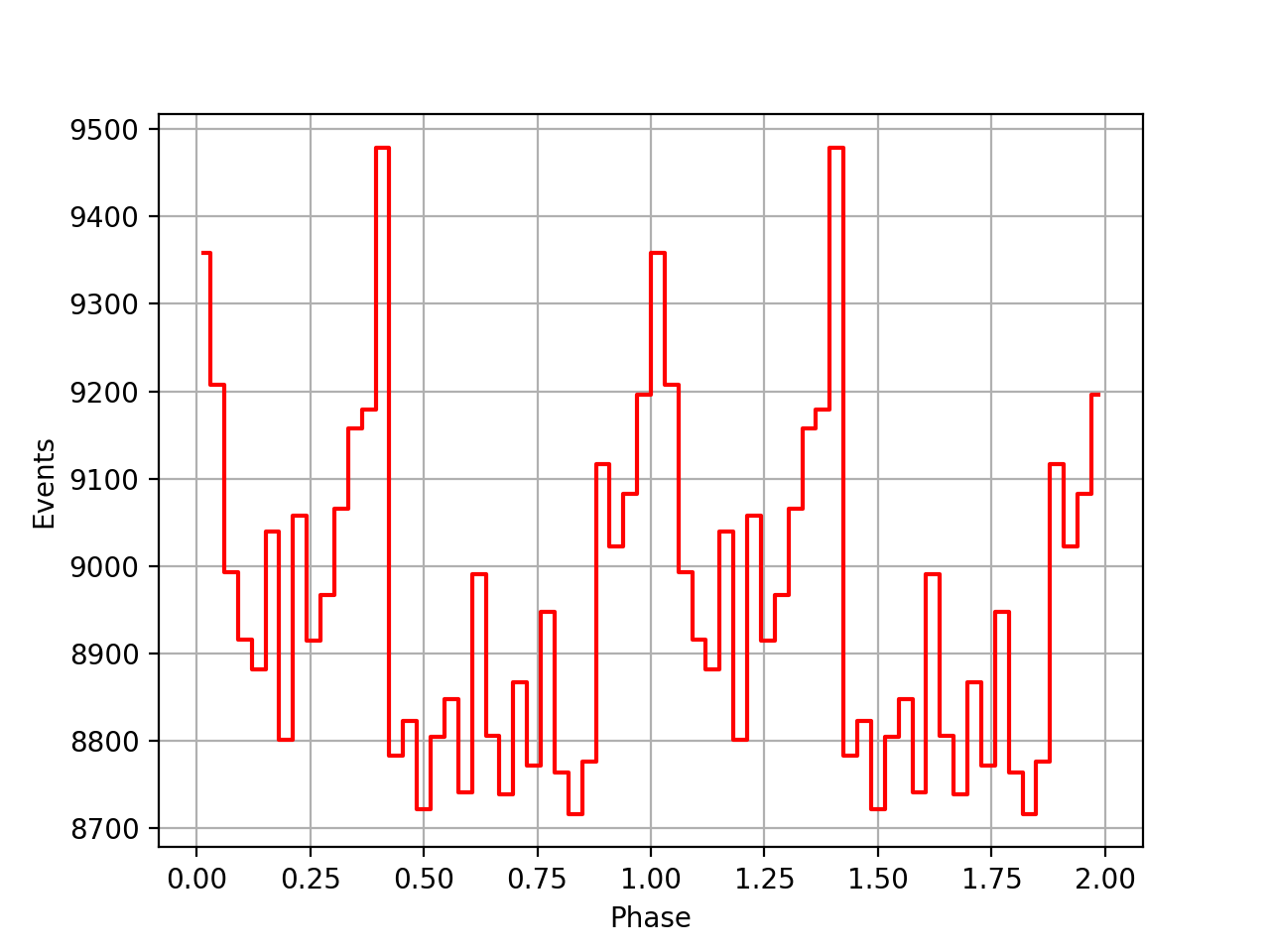 |
#40
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
- File pulsar_vp0001_0337_0616_xte.psrtime_20220118T1626.png added
- File pulsar_vp0001_xte.psrtime_20220118T1626.png added
- File pulsar_vp0337_xte.psrtime_20220118T1626.png added
- File pulsar_vp0616_xte.psrtime_20220118T1626.png added
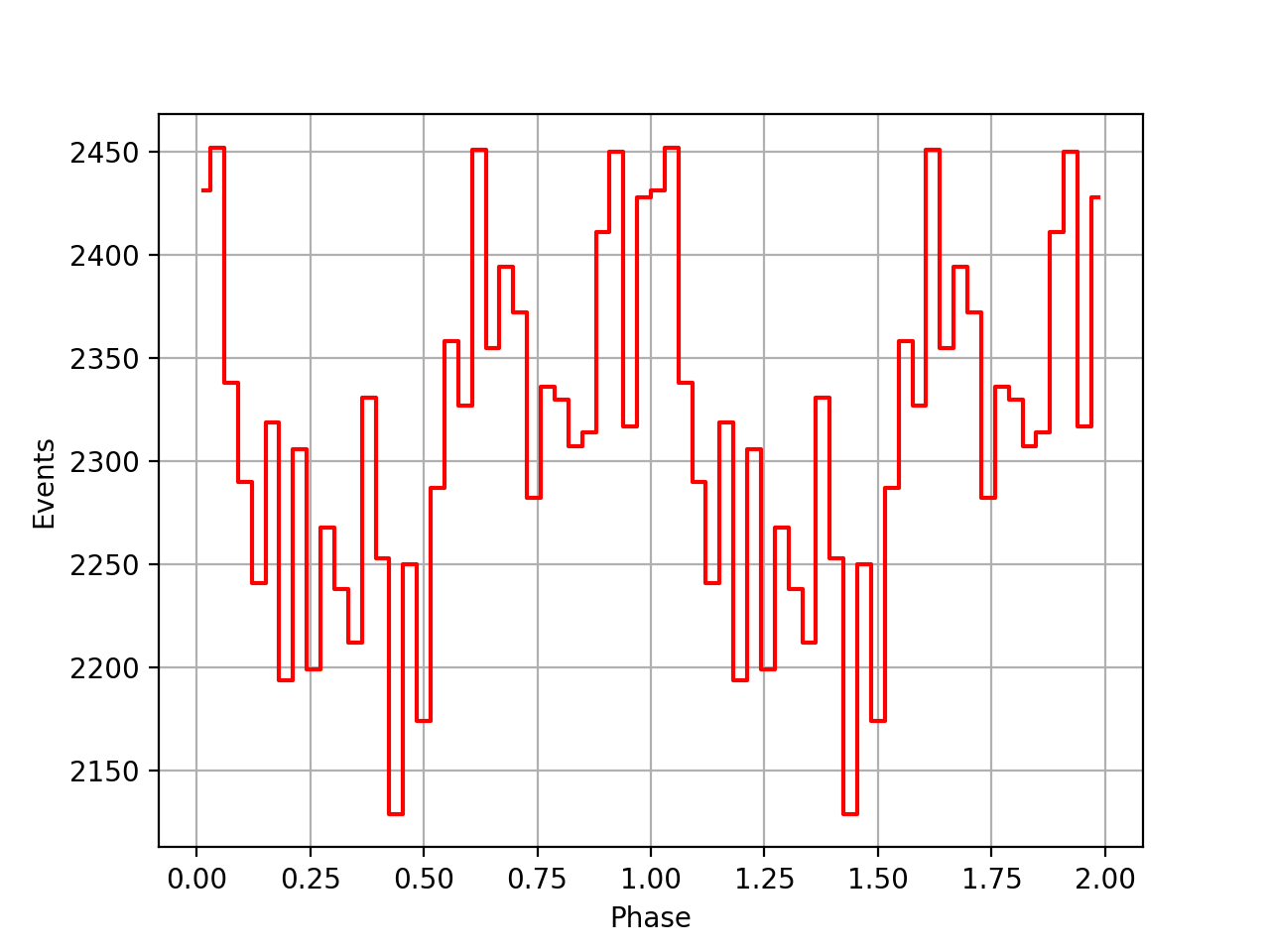
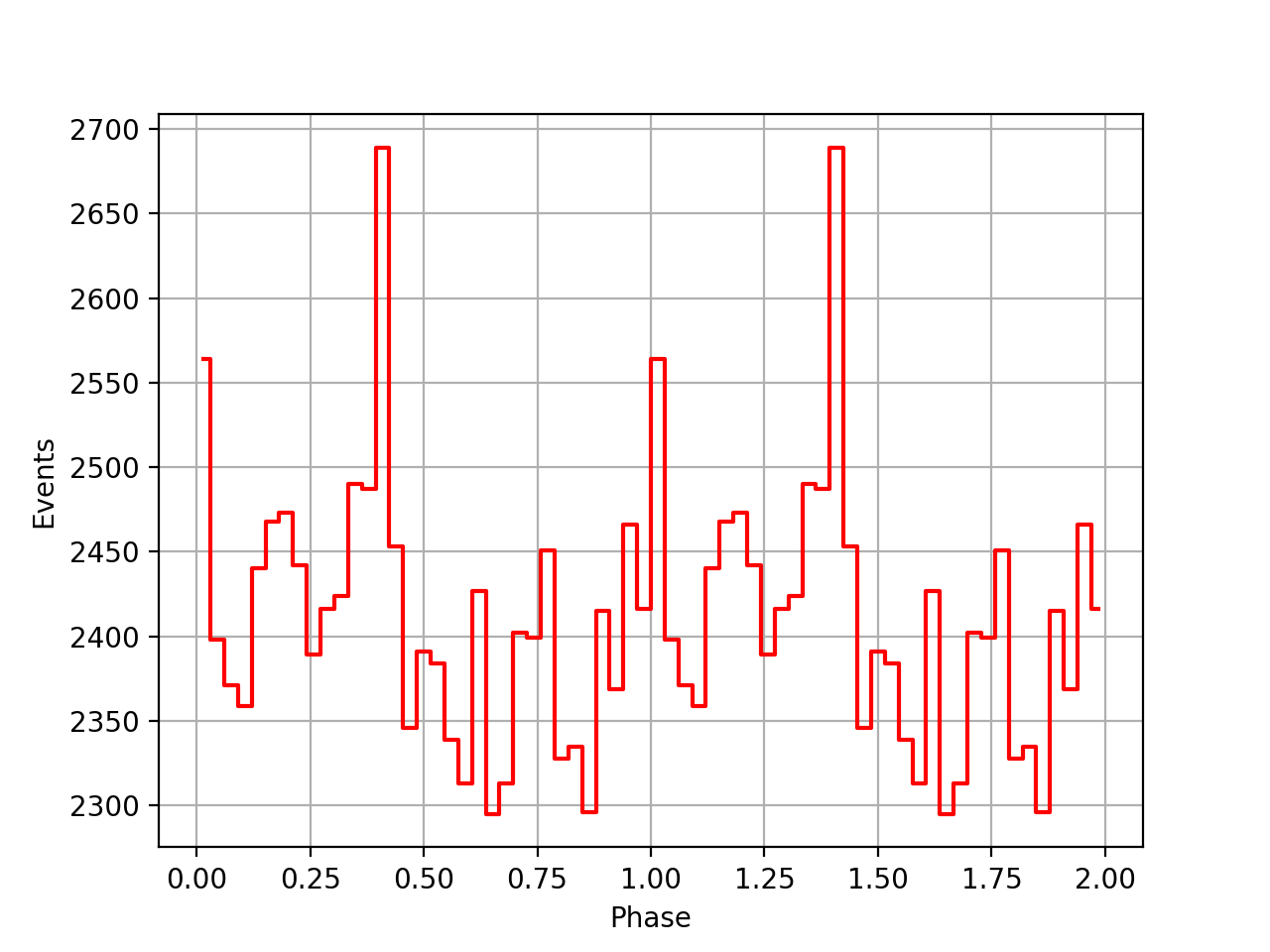
I redid the same phase curve analysis using the ephemerides found in the ftools/xte package. They seem to behave much better, the pulses between the viewing periods are nicely aligned, the summed phase curve becomes really a nice Crab phase curve.
| VP0001 | VP0337 | VP0616 | All |
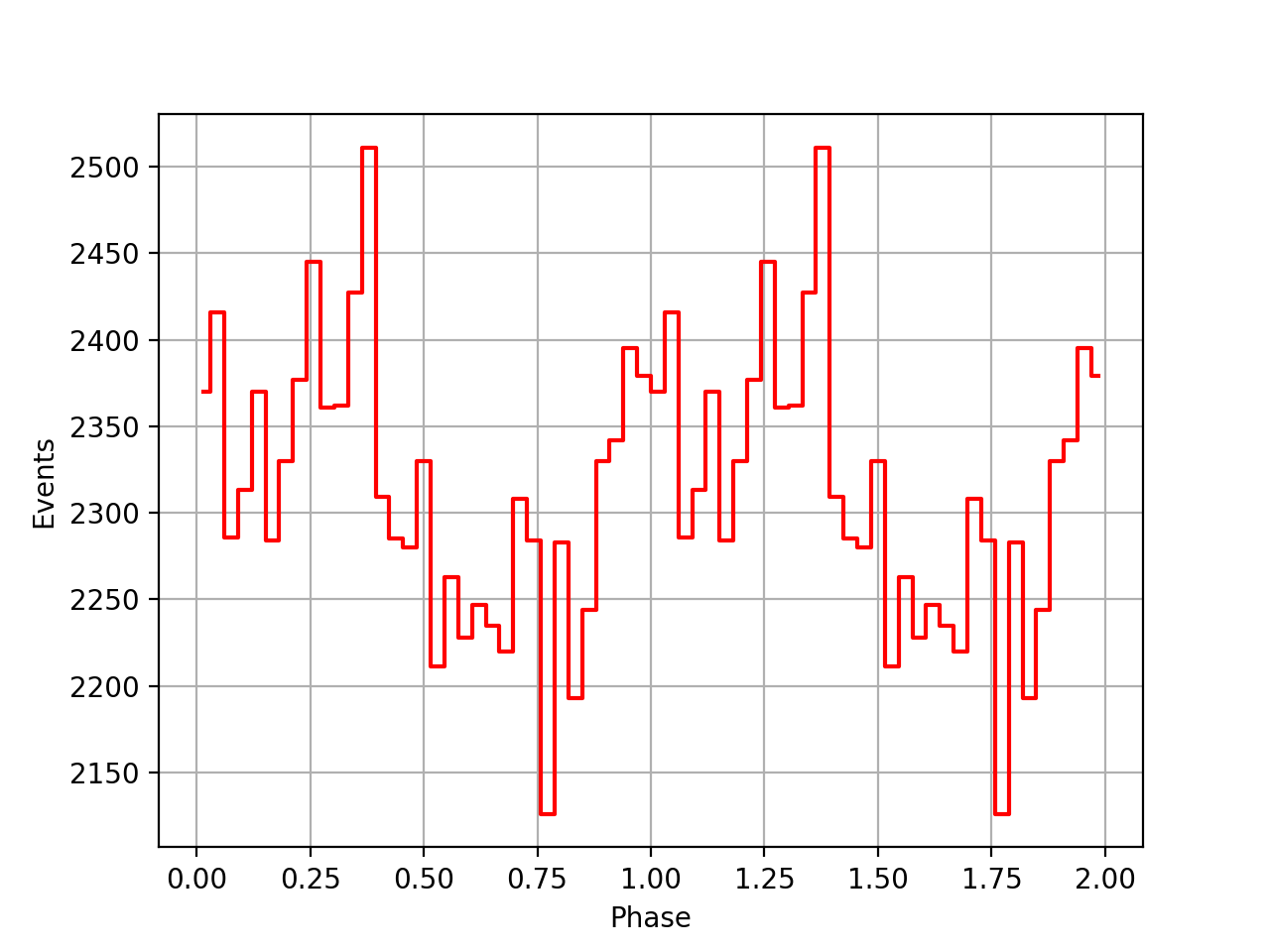 |
 |
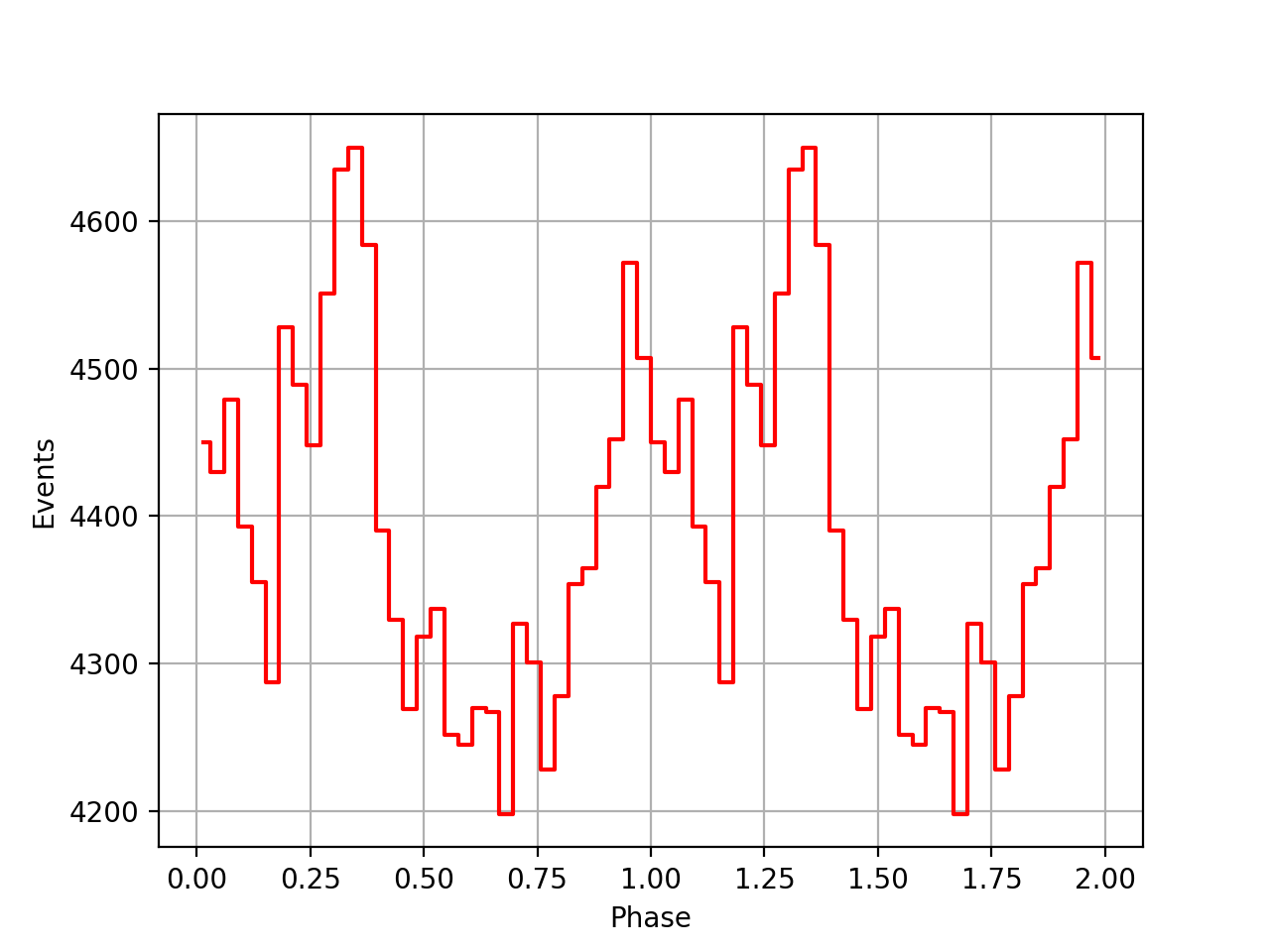 |
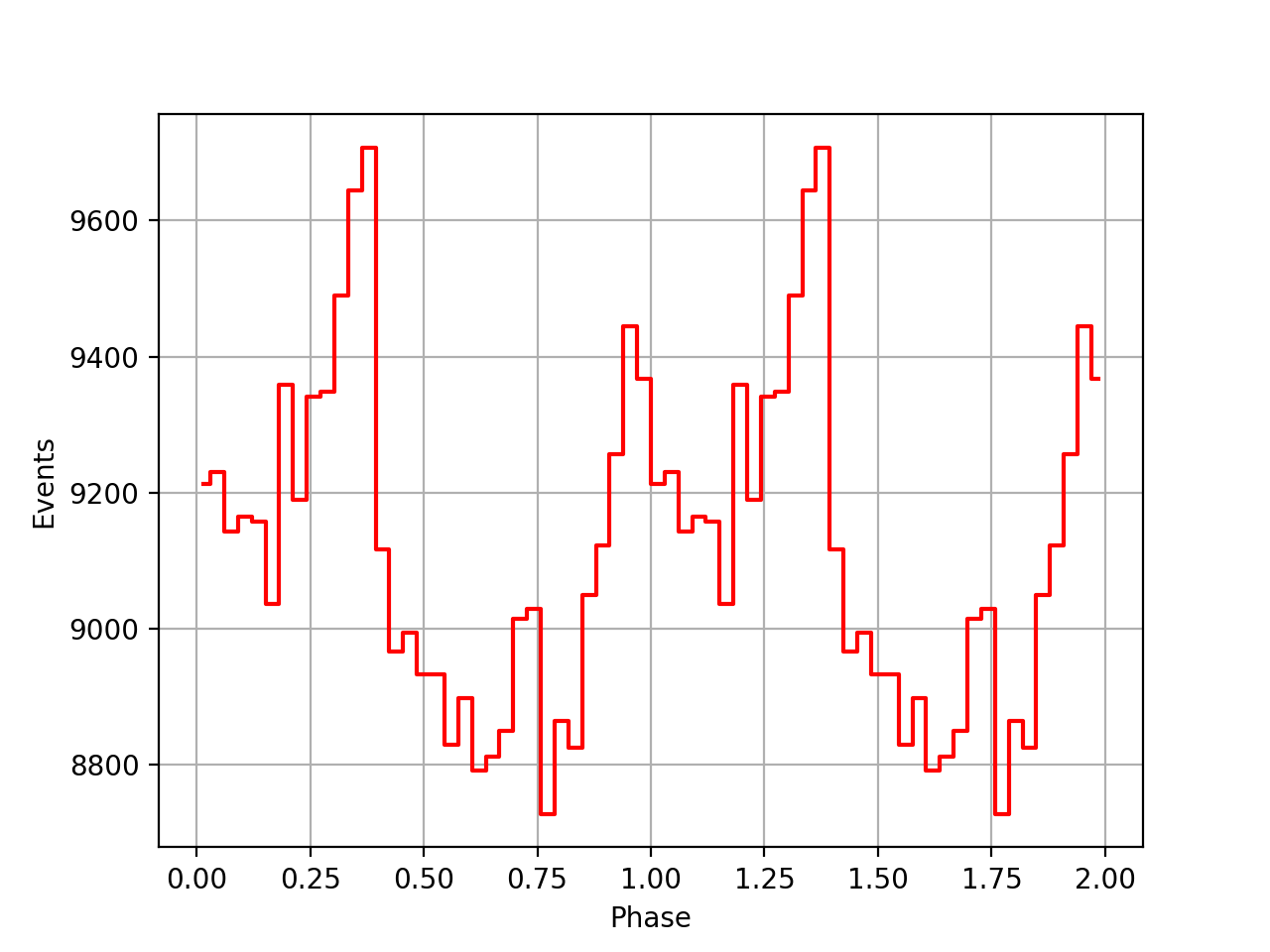 |
#41
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
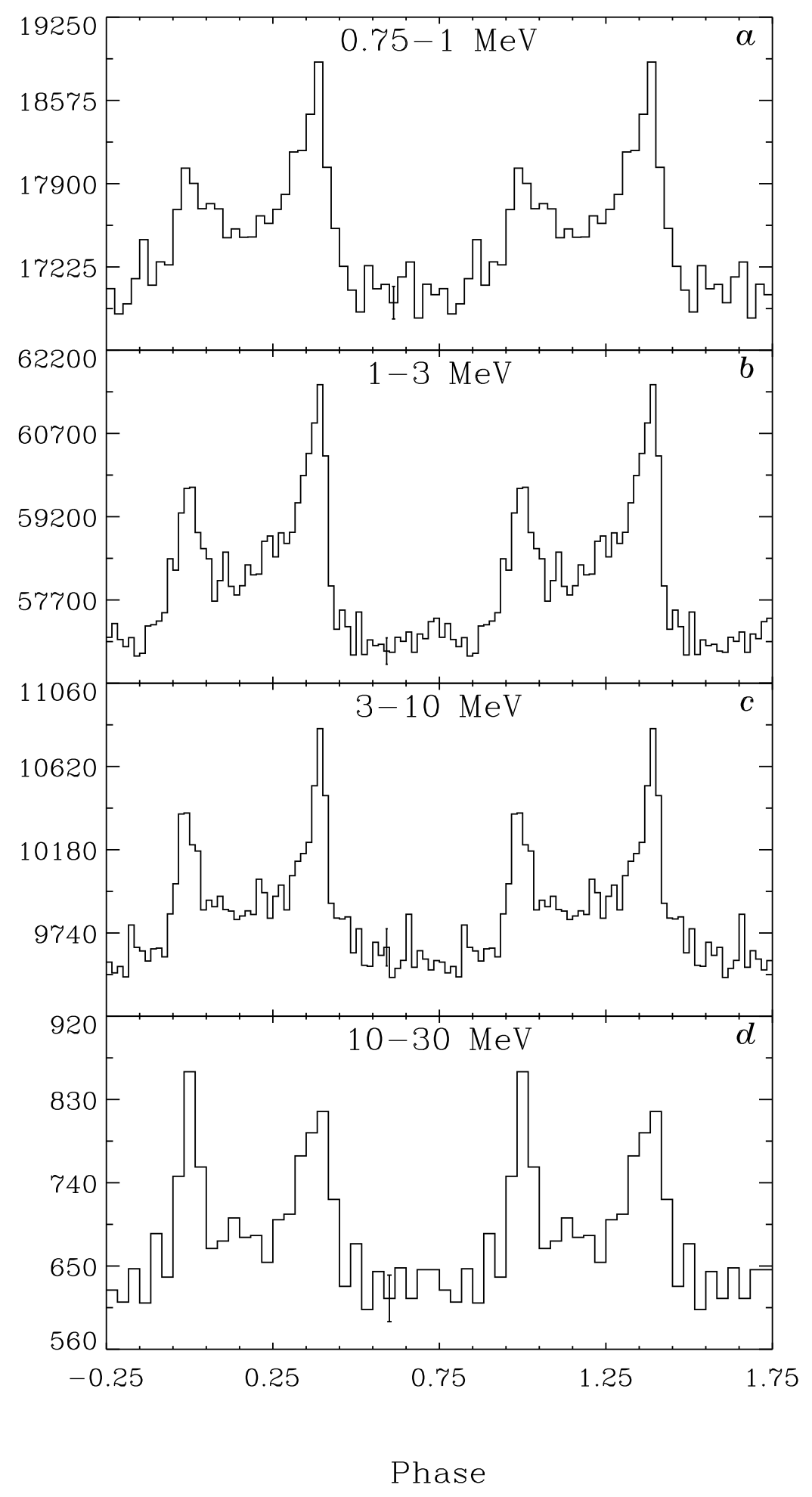
- File crab_kuiper_2001.png added
Here a comparison of the summed phase curve with that obtained by Kuiper et al. (2001), A&A, 378, 918. The alignment of the pulses is quite good. I probably will be able to reproduce Lucien’s figure for the GammaLib validation paper.
 |
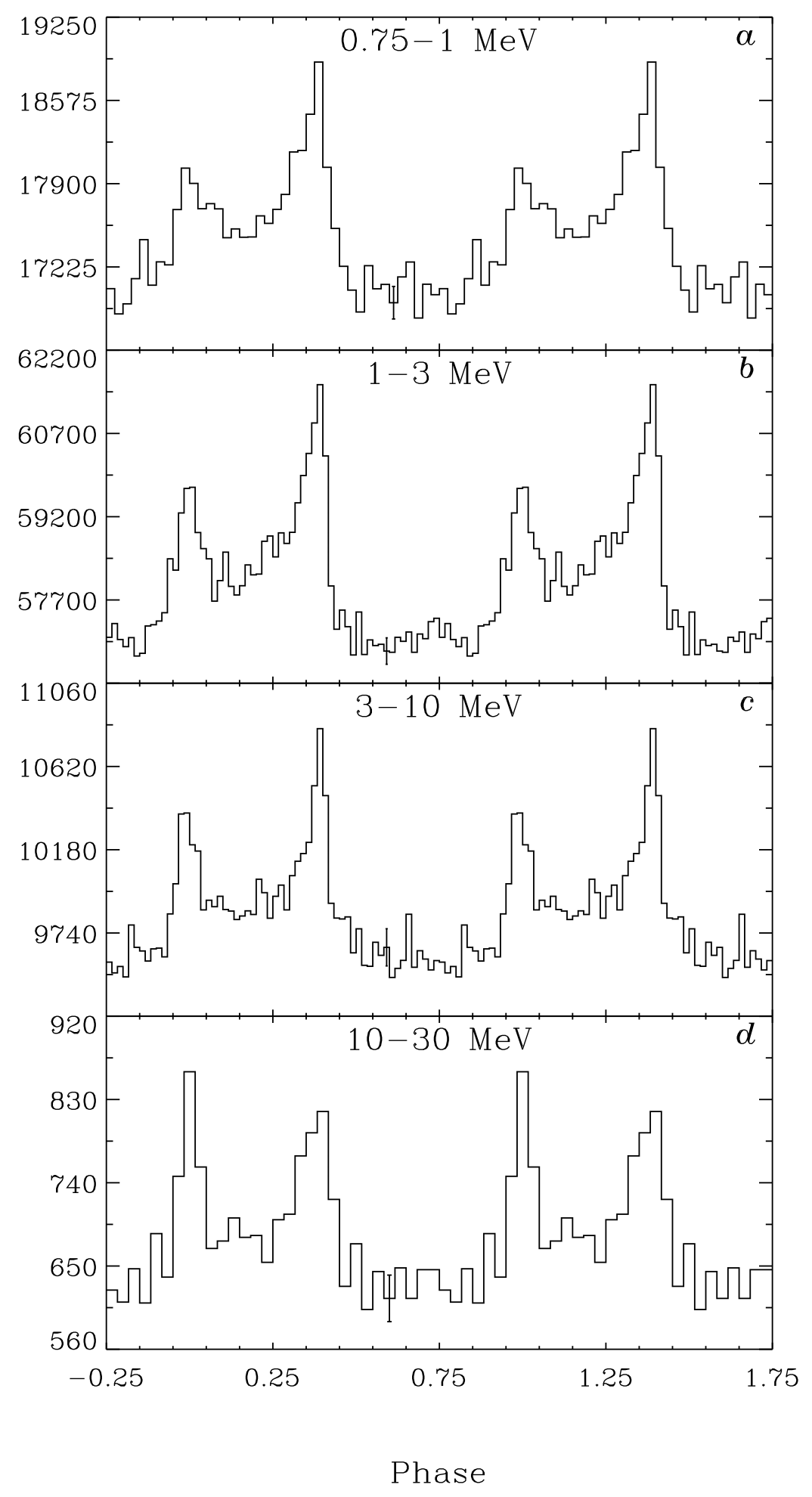 |
#42
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
- File pulsar_vp0001_0337_0616_xte.psrtime_bvc.png added
- File pulsar_vp0001_0337_0616_xte.psrtime_nobvc.png added
- File pulsar_vp0001_xte.psrtime_bvc.png added
- File pulsar_vp0001_xte.psrtime_nobvc.png added
- File pulsar_vp0337_xte.psrtime_bvc.png added
- File pulsar_vp0337_xte.psrtime_nobvc.png added
- File pulsar_vp0616_xte.psrtime_bvc.png added
- File pulsar_vp0616_xte.psrtime_nobvc.png added
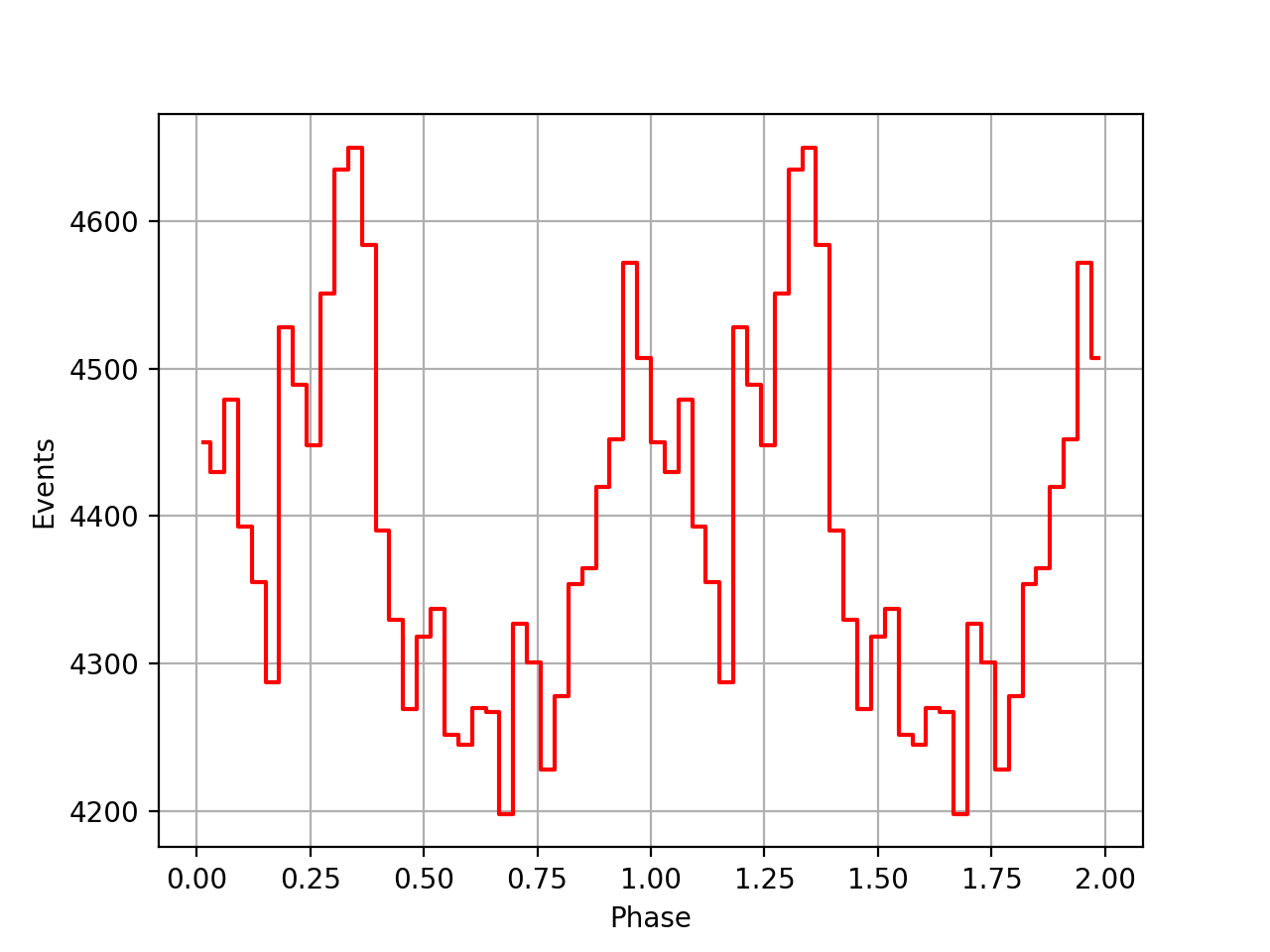
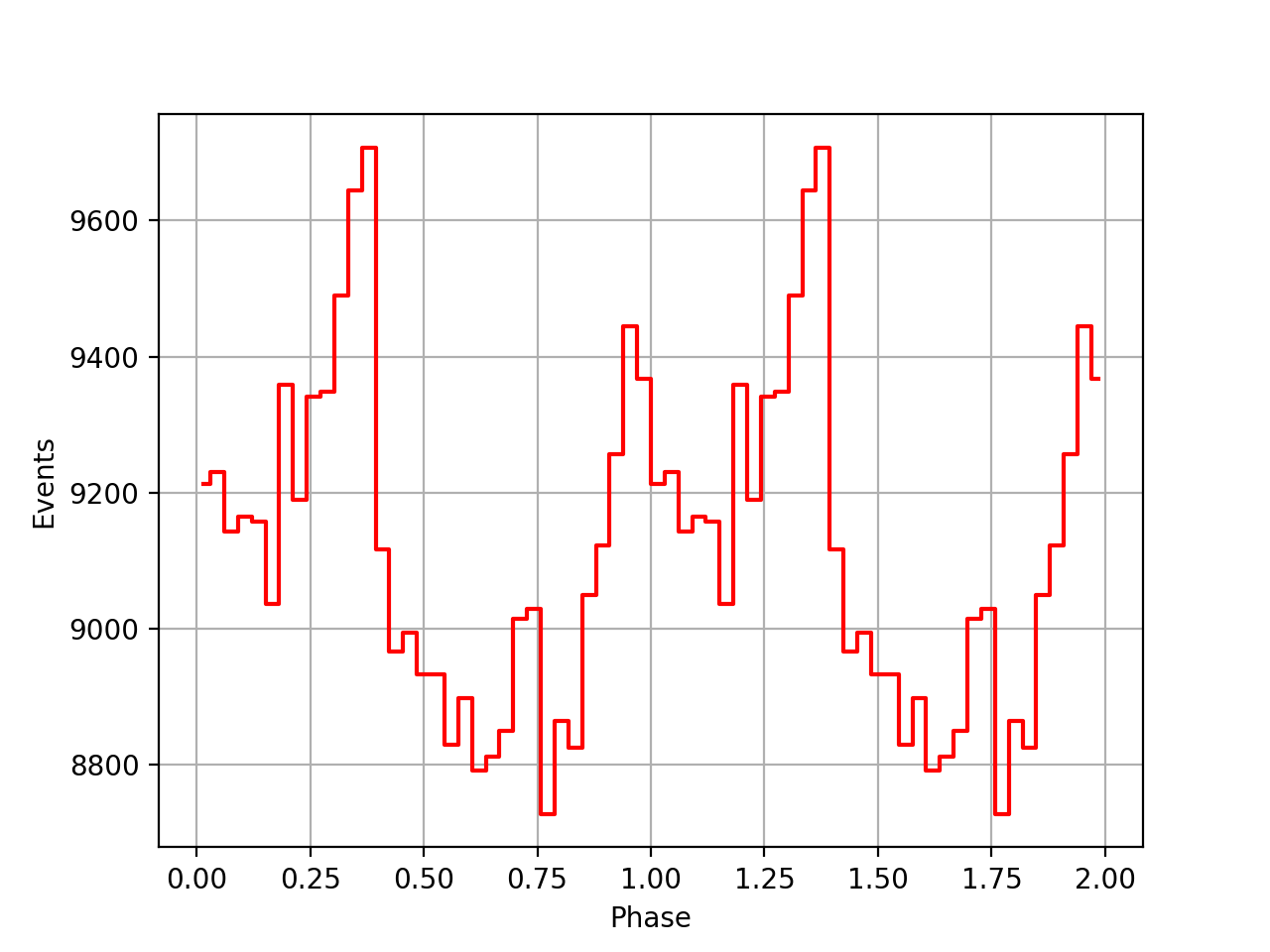
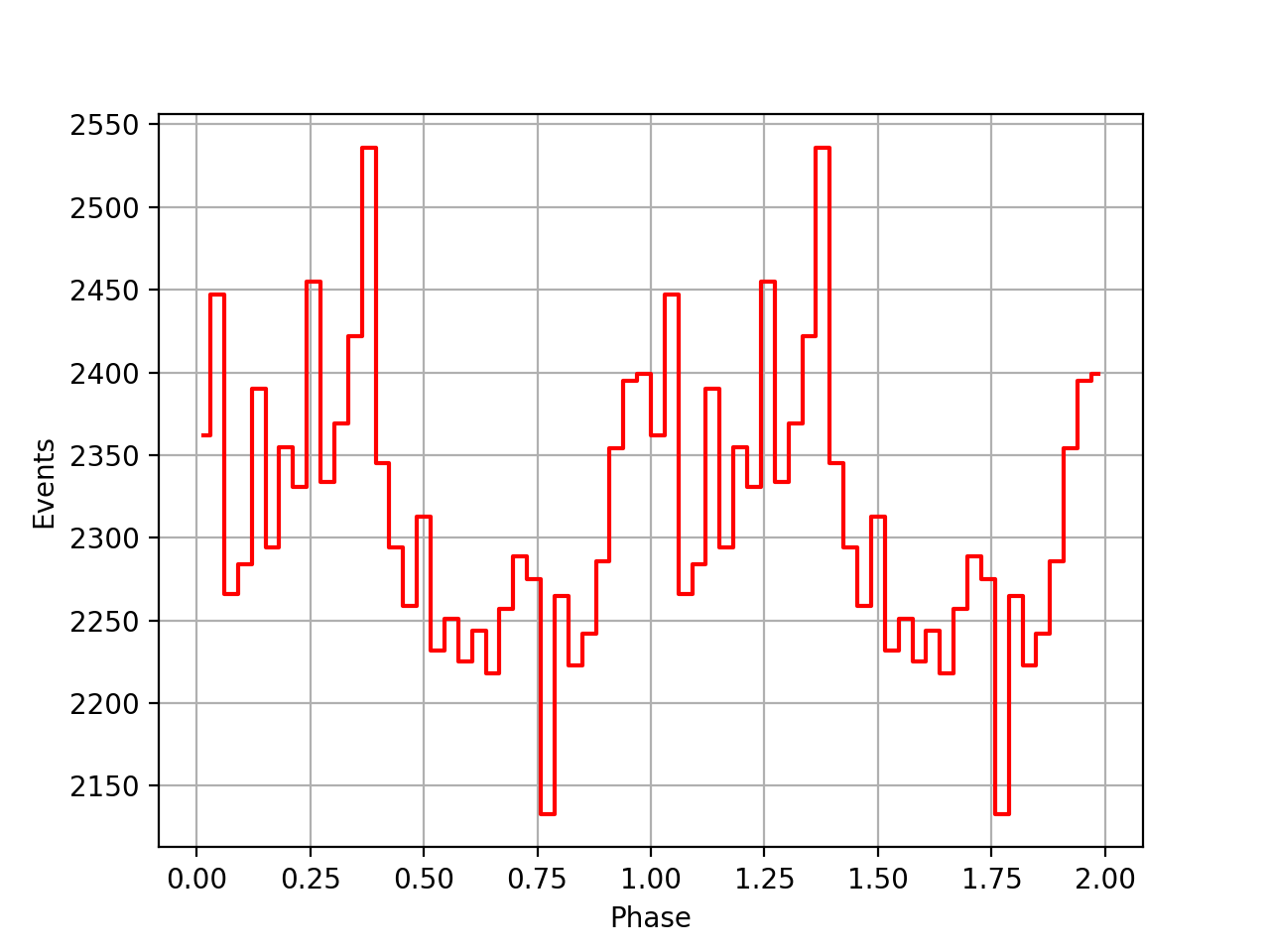
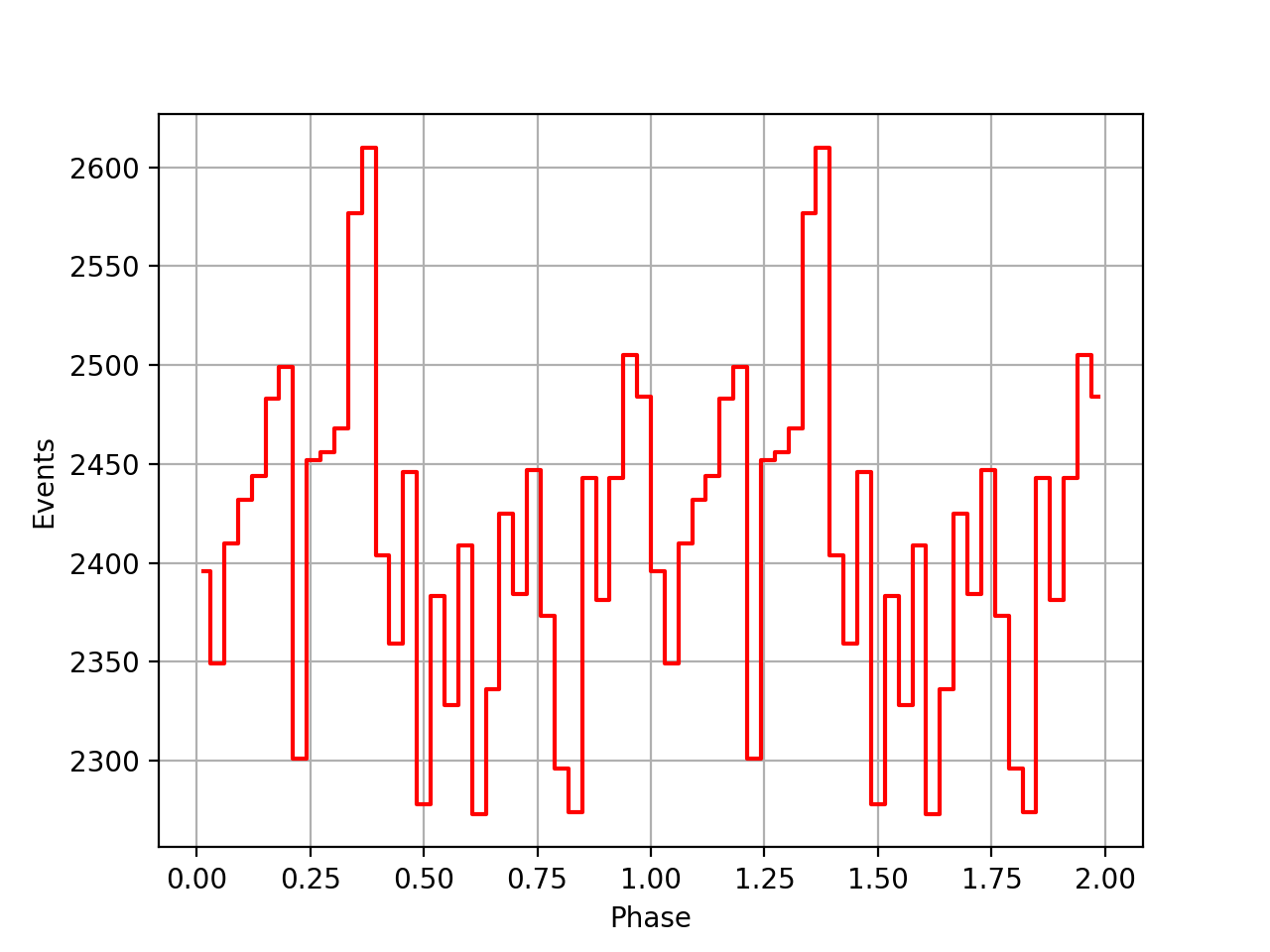
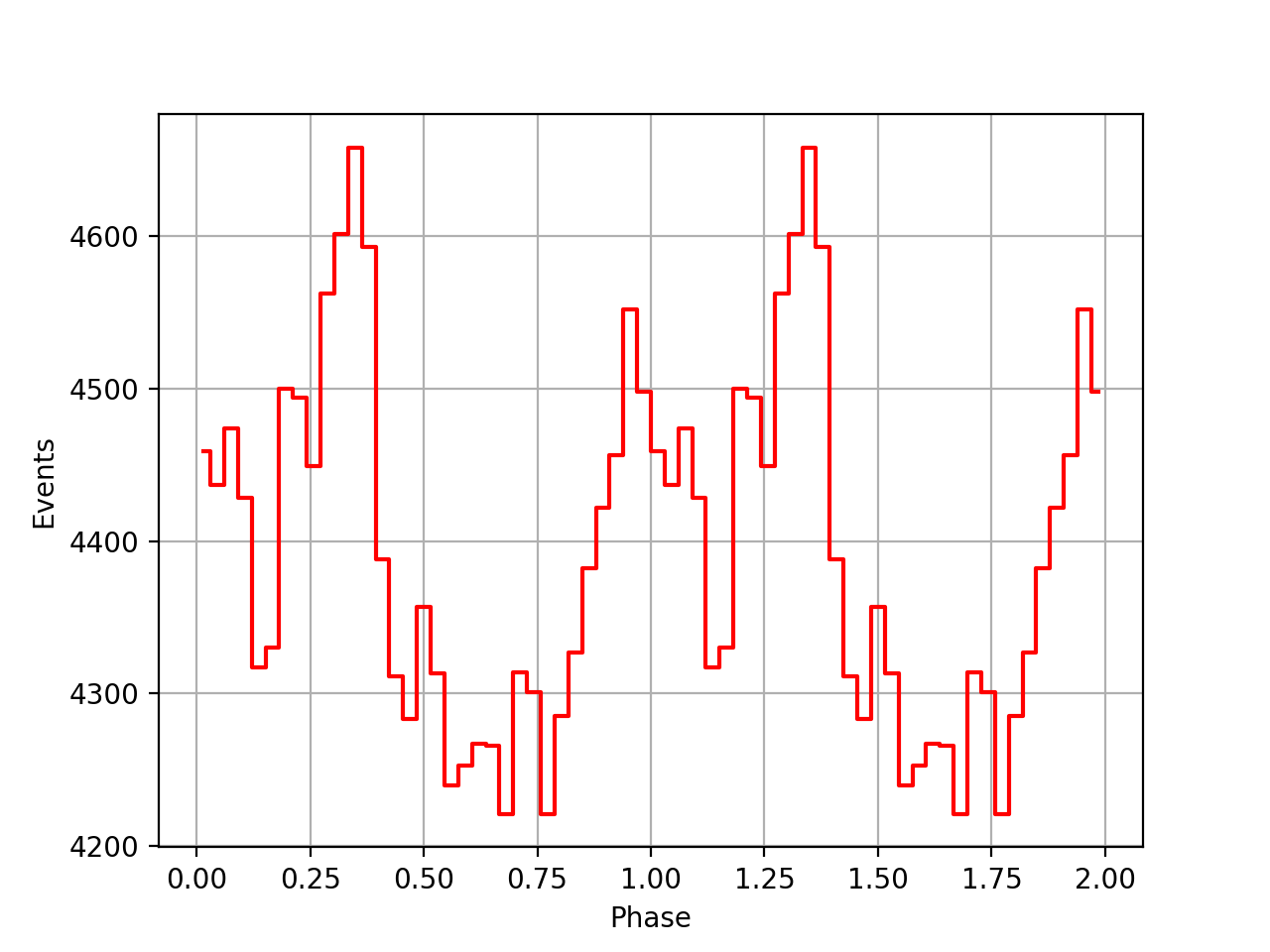
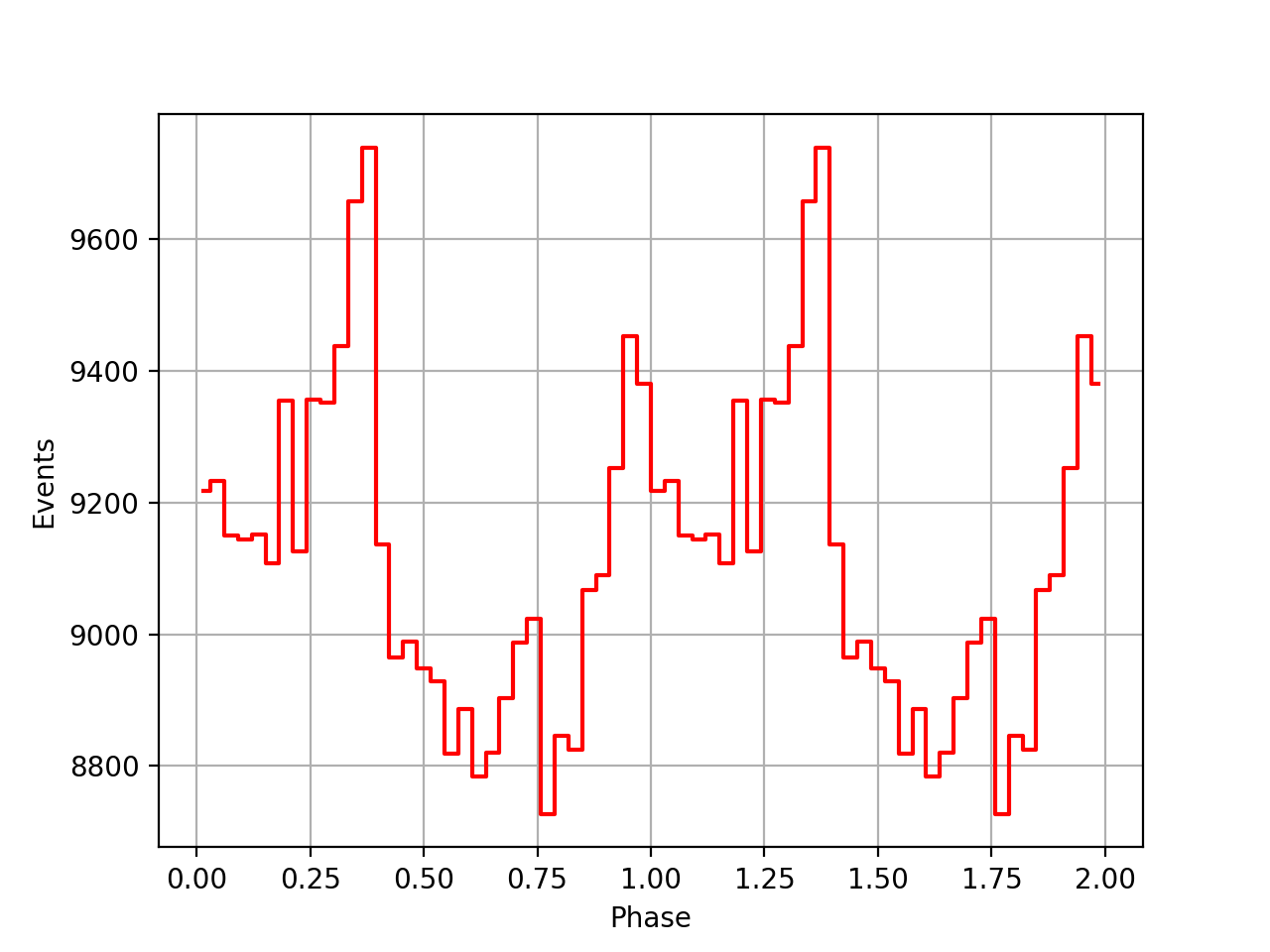
I implemented a new method GEphemerides::geo2sbb() that allows to compute the BVC correction on-the-fly without referring to a BVC file. This is useful since there seem to be BVC data for all viewing periods. Below a comparison of the phase curves obtained using the BVC data, and without using the BVC data. Overall the phase curves are comparable, yet the peaks without the BVC data seem to be more narrow.
| VP0001 | VP0337 | VP0616 | All |
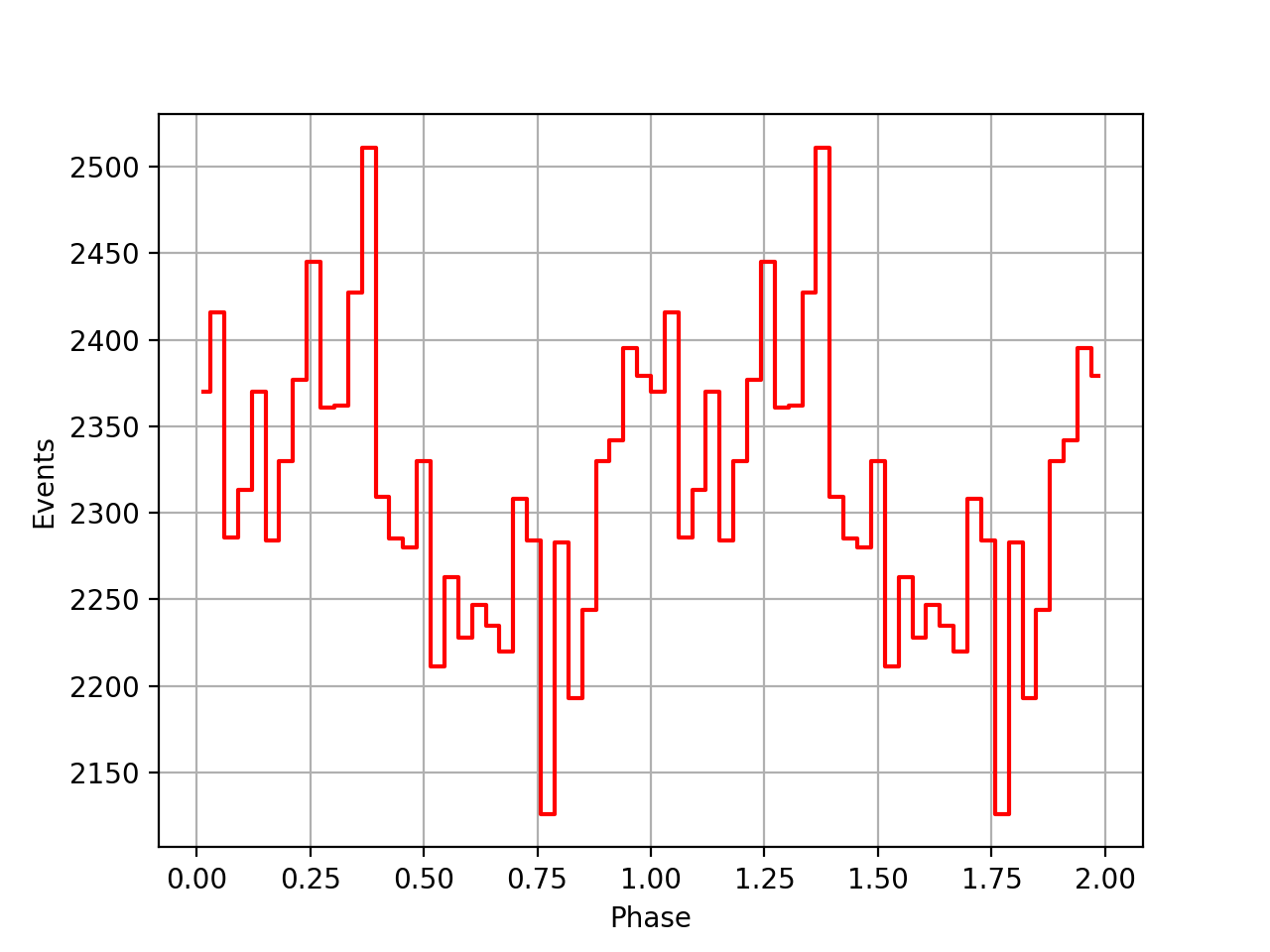 |
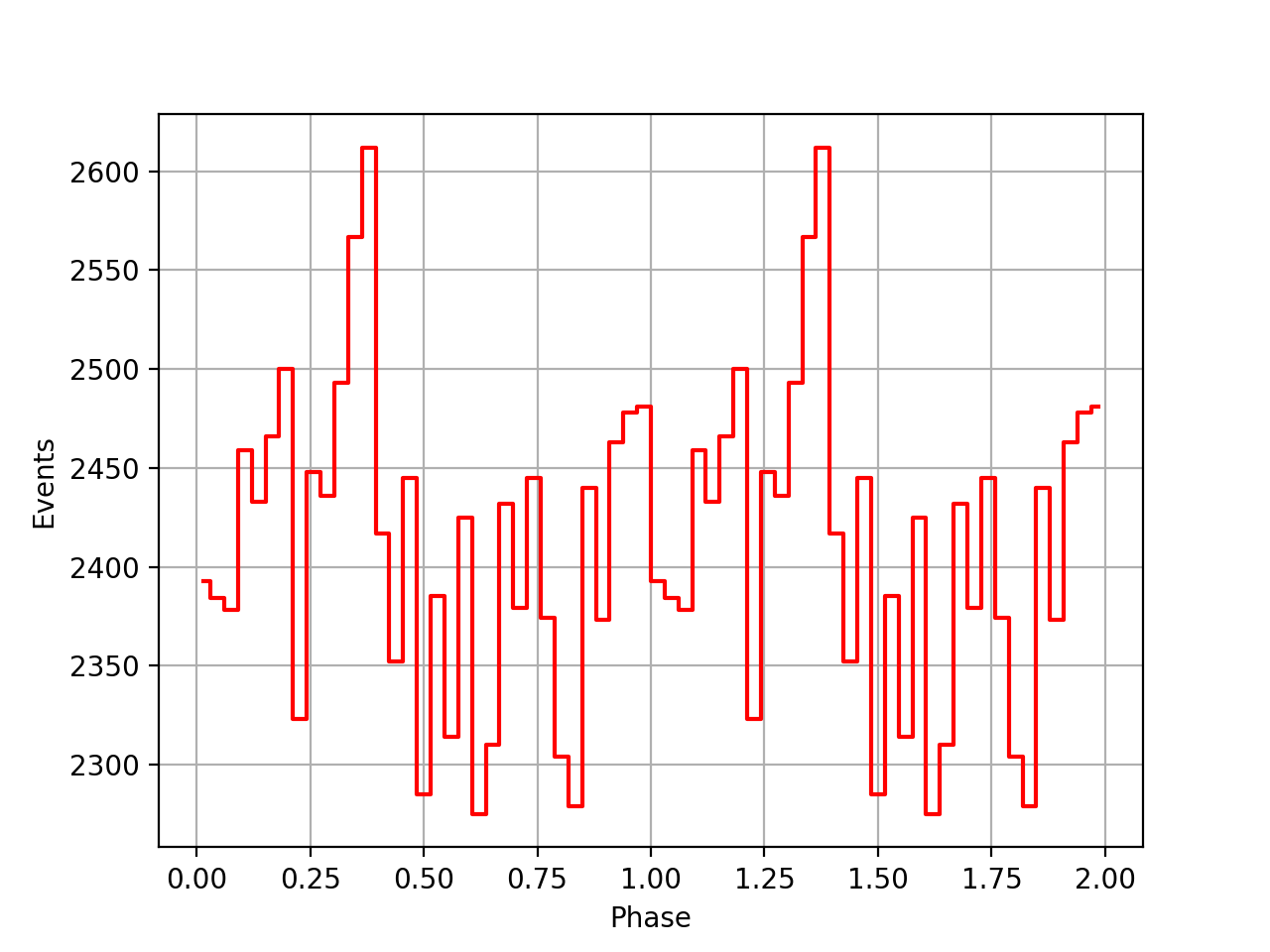 |
 |
 |
 |
 |
 |
 |
#43
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
- File crab_dri10_bvc.png added
- File crab_dri10_nobvc.png added
- % Done changed from 70 to 80
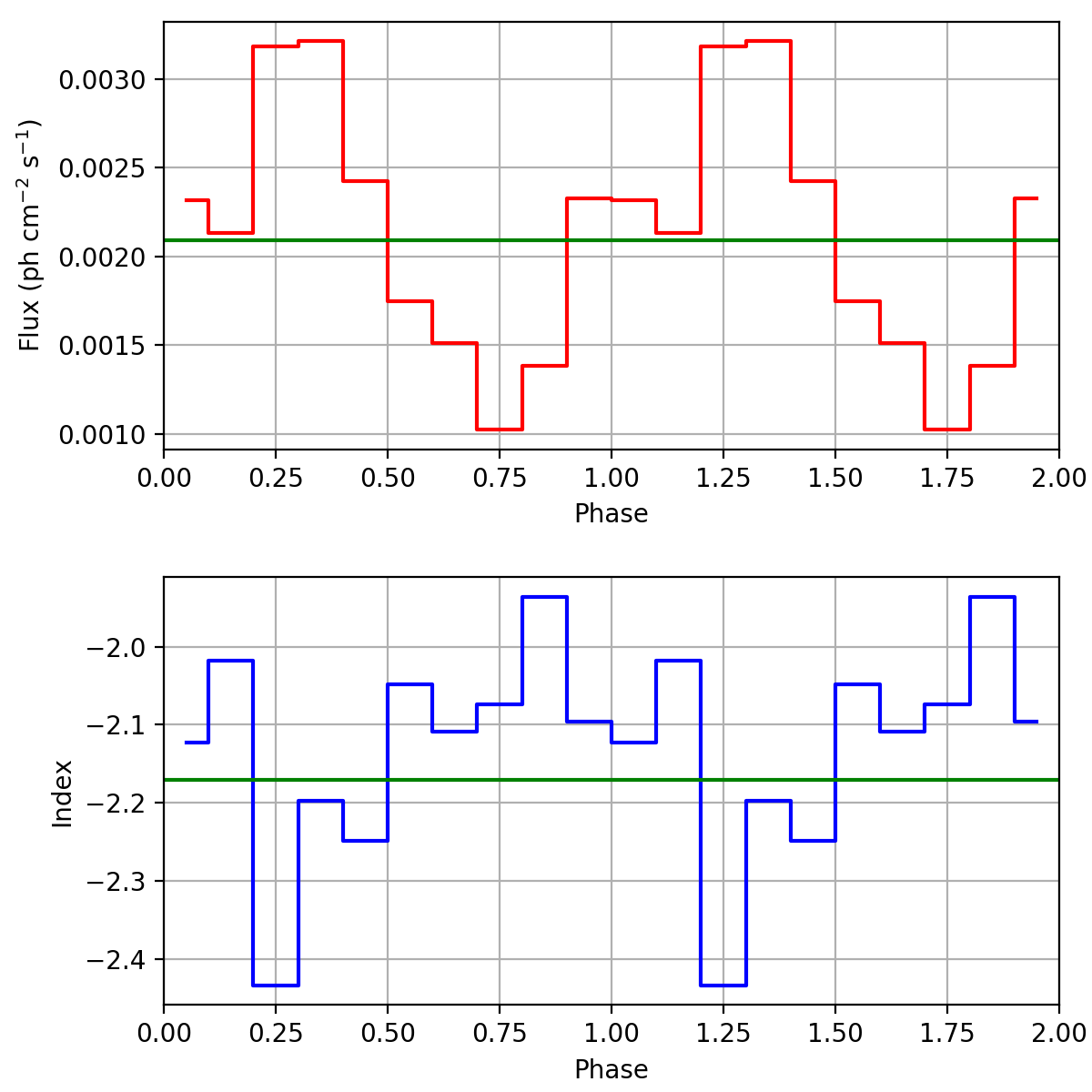
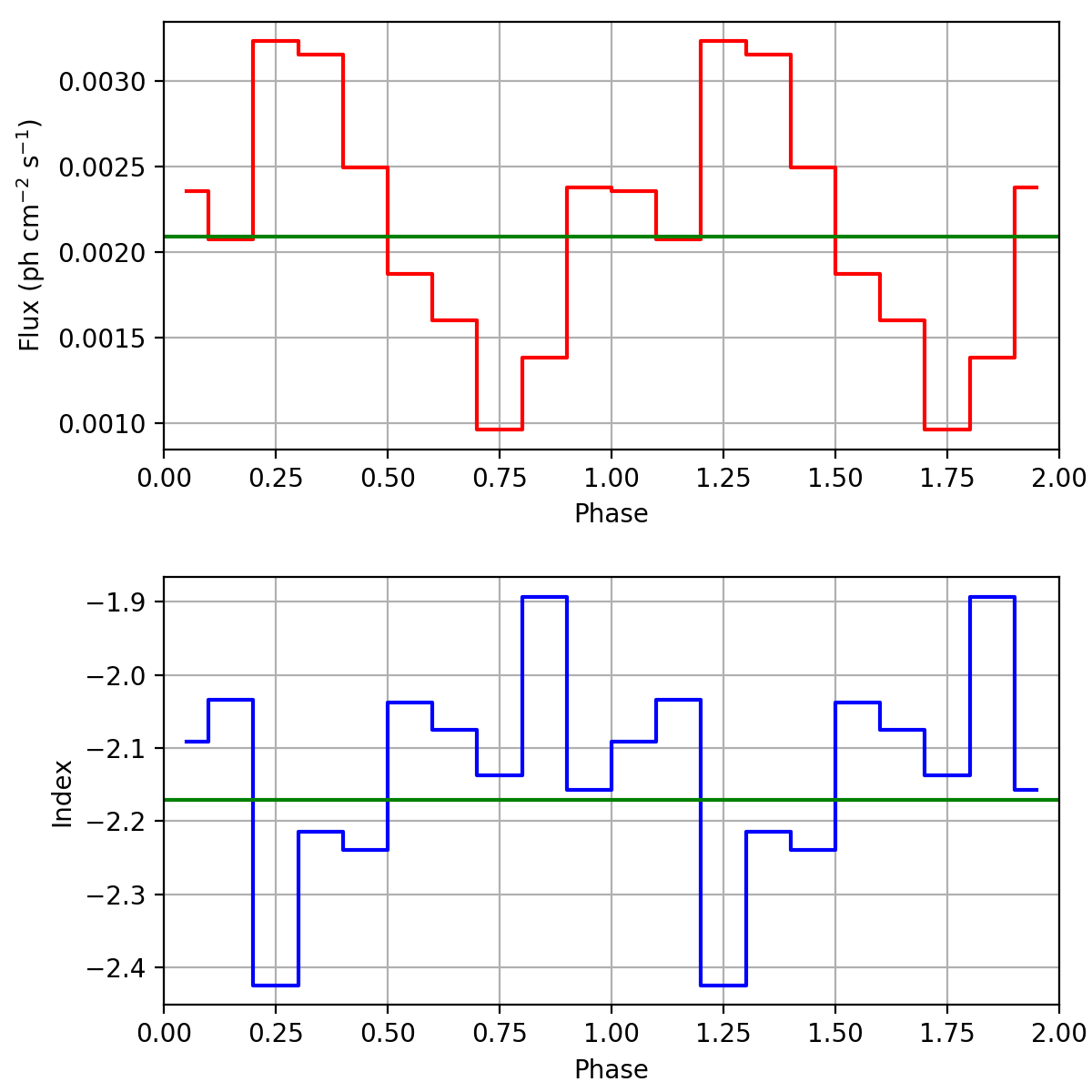
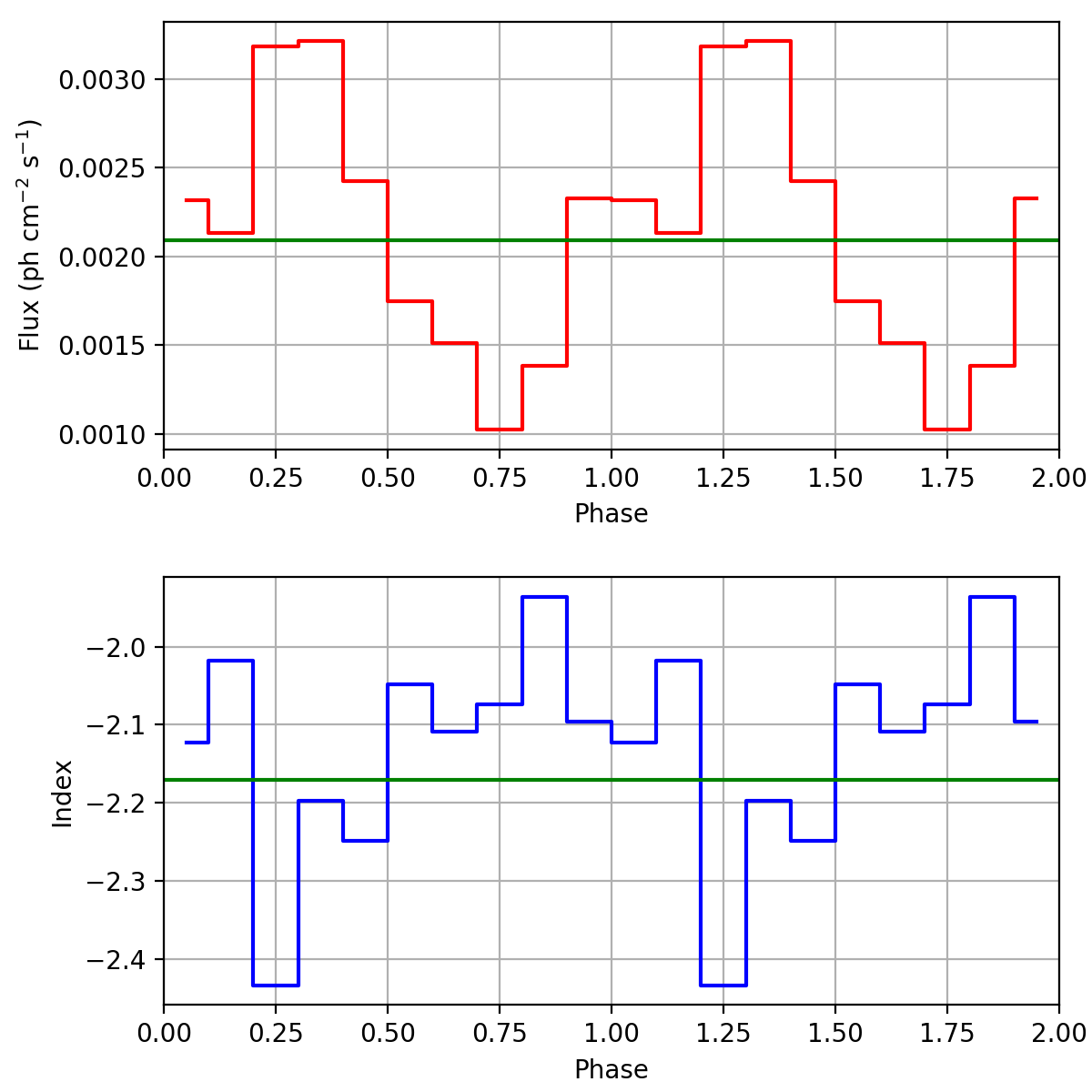
I now did a full-blown 4D analysis using the pulsar handling in GCOMDri::compute_dre, GCOMDri::compute_drx and GCOMDri::compute_drg and in comobsbin. I analysed the data for VP0001 in 10 phase bins and the four standard energy bins. I selected zetamin=5 and fpmtflag=0. A standard SRCLIX analysis was performed, using navgr=3 and nincl=13. I used the XTE pulsar ephemerides. For comparison, I did the analysis using both the BVC file information and on-the-fly Barycentre correction computation. The results are shown in the figures below, where the top plot shows the 0.75-30 MeV flux as function of the phase, while the bottom plot shows the power law spectral index as function of phase. Both phase curves are very similar, and as expected, the spectrum in the (second) pulse is a bit softer. This looks also very reasonable.
| BVC | On-the-fly computation |
 |
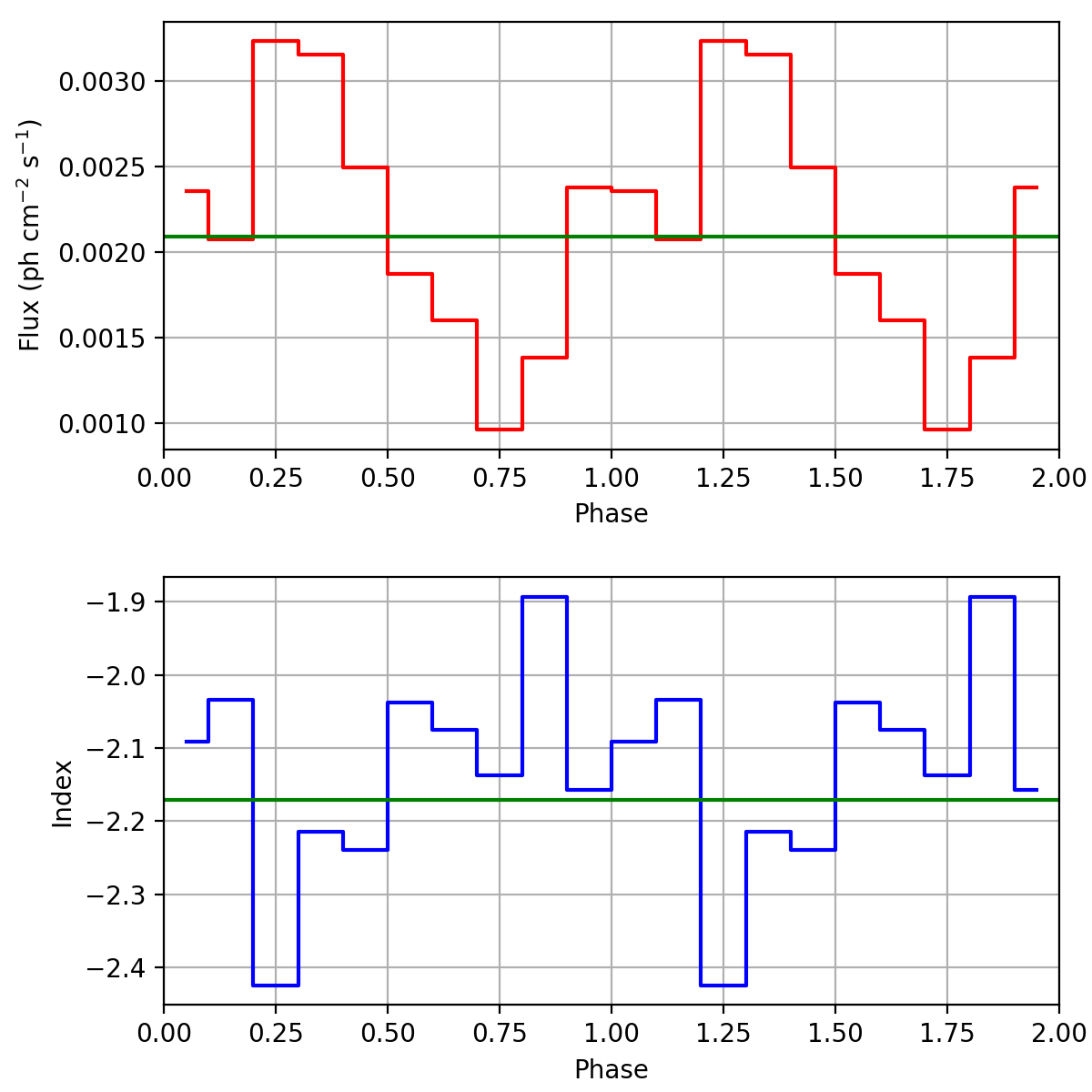 |
I still need to verify that the flux is correct (i.e. the flux correction is applied correctly).
Once this is done this feature can be merged in, after adding a few unit tests for the new methods.
#44
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
- File crab_dri10_bvc.png added
- File crab_dri10_nobvc.png added
- % Done changed from 80 to 90
I checked that the fluxes and indices vary around the average values, shown as green lines in the figures above. The flux correction works.
#45
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
- File deleted (
crab_dri10_bvc.png)
#46
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
- File deleted (
crab_dri10_nobvc.png)
#47
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
- File crab_pulsar.png added
- Status changed from In Progress to Closed
- % Done changed from 90 to 100
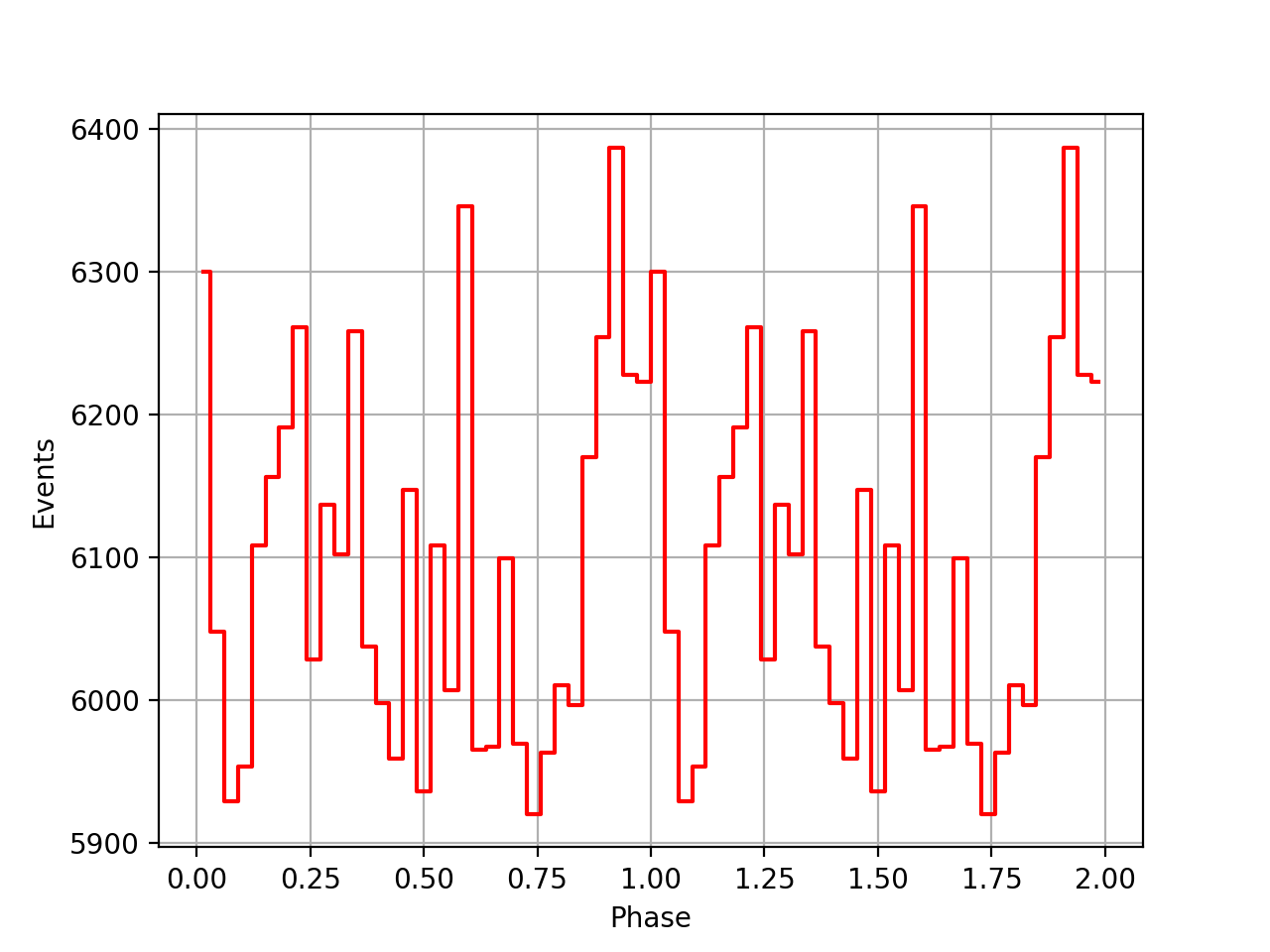
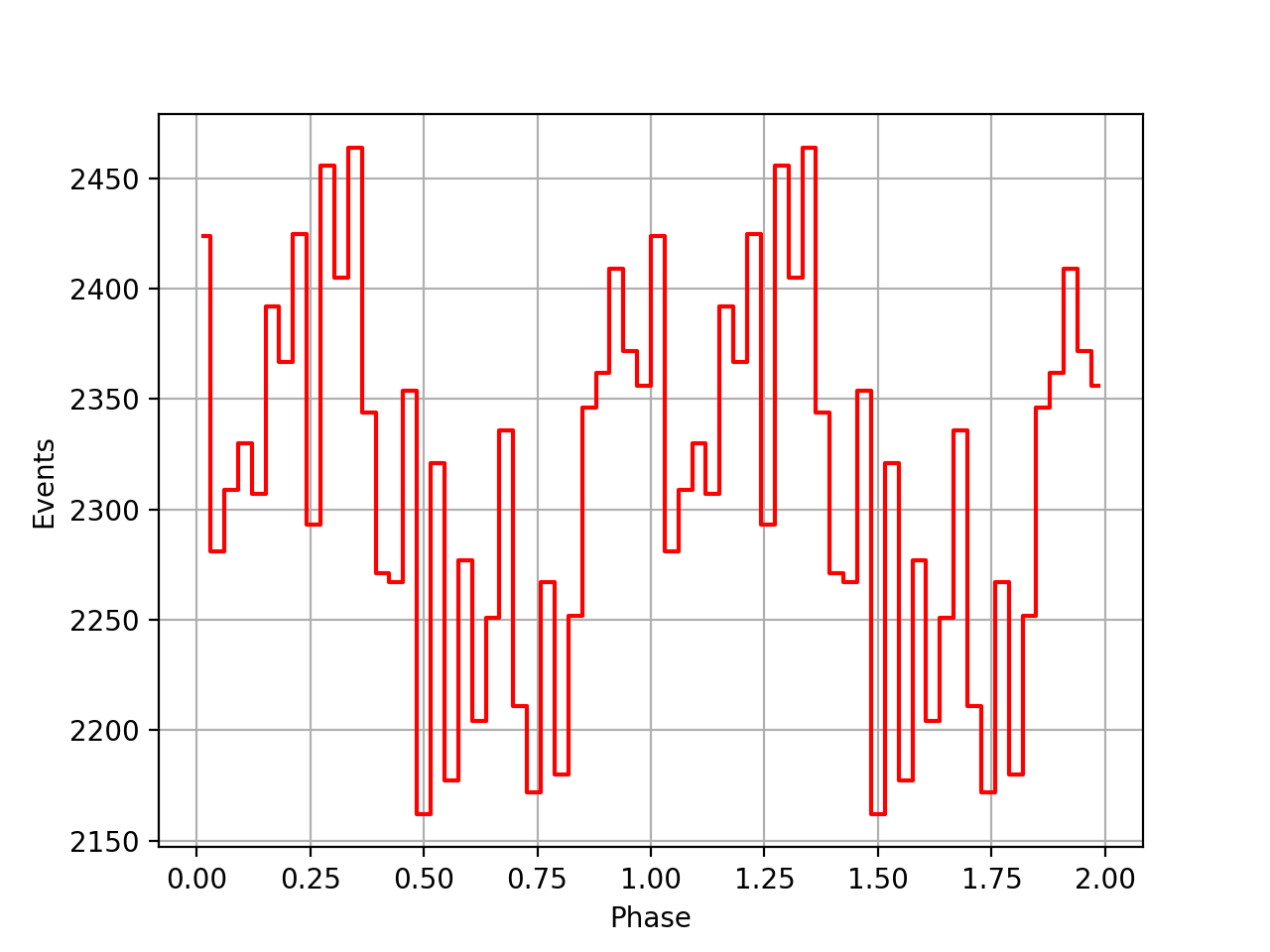
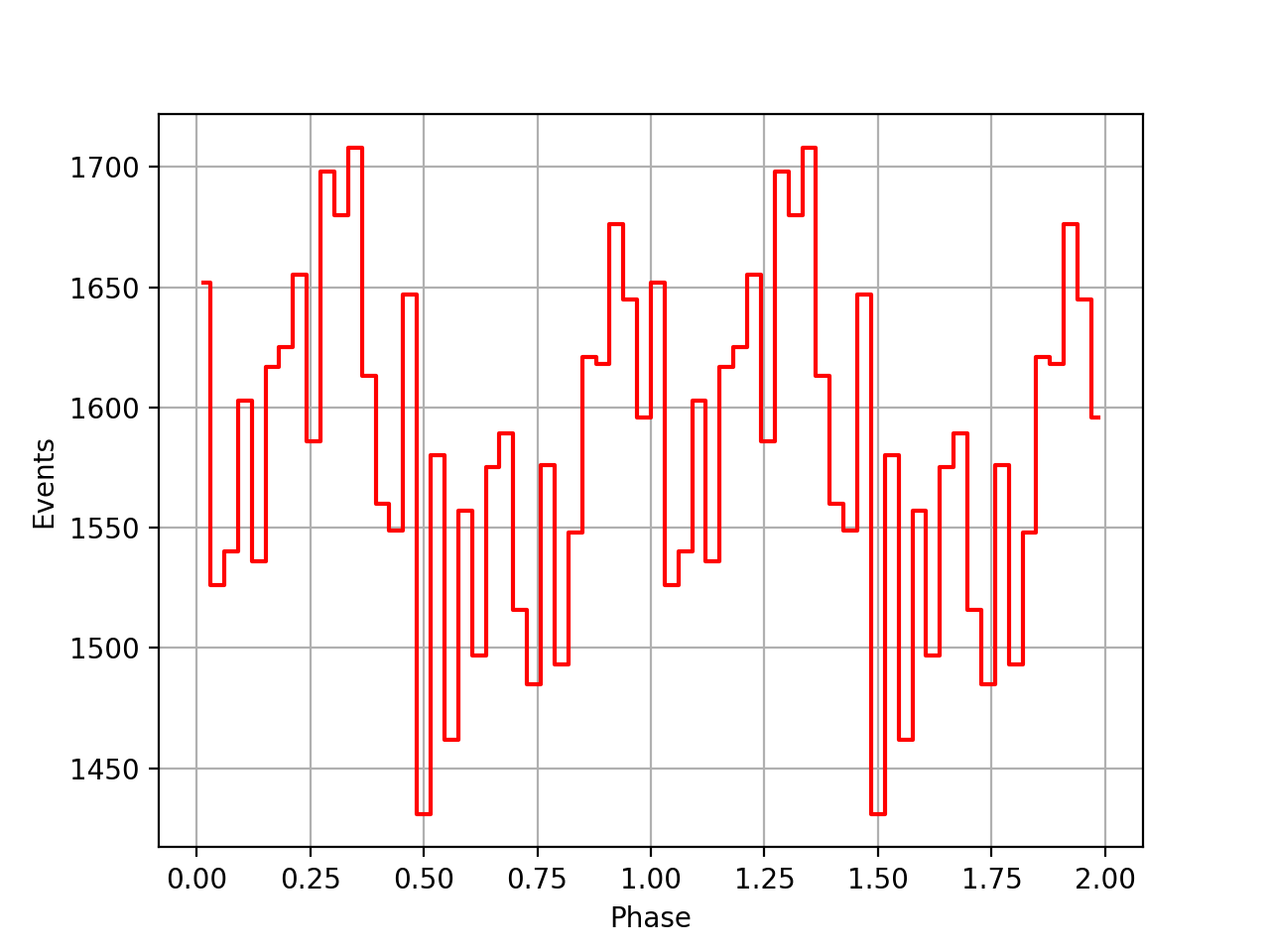
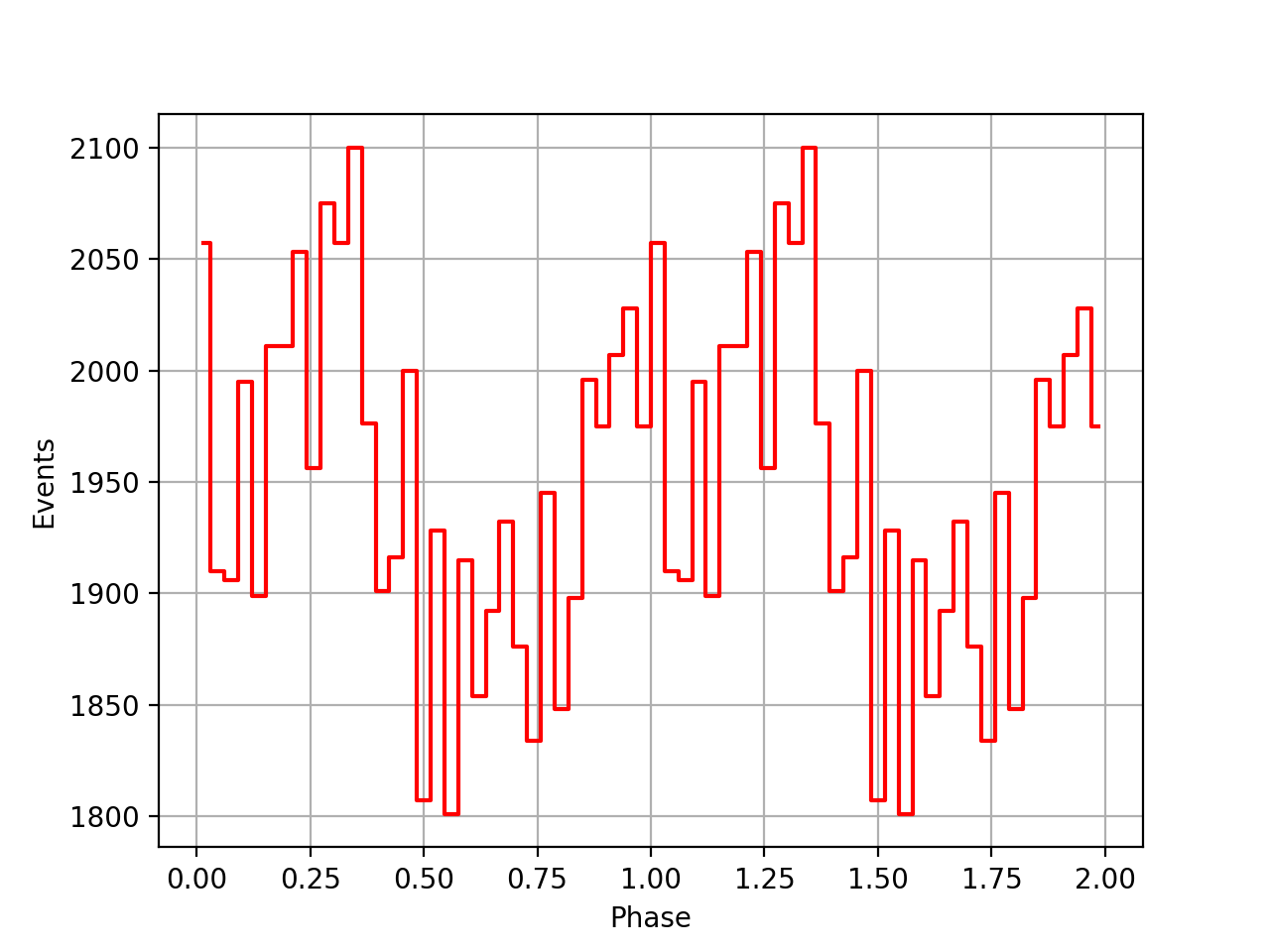
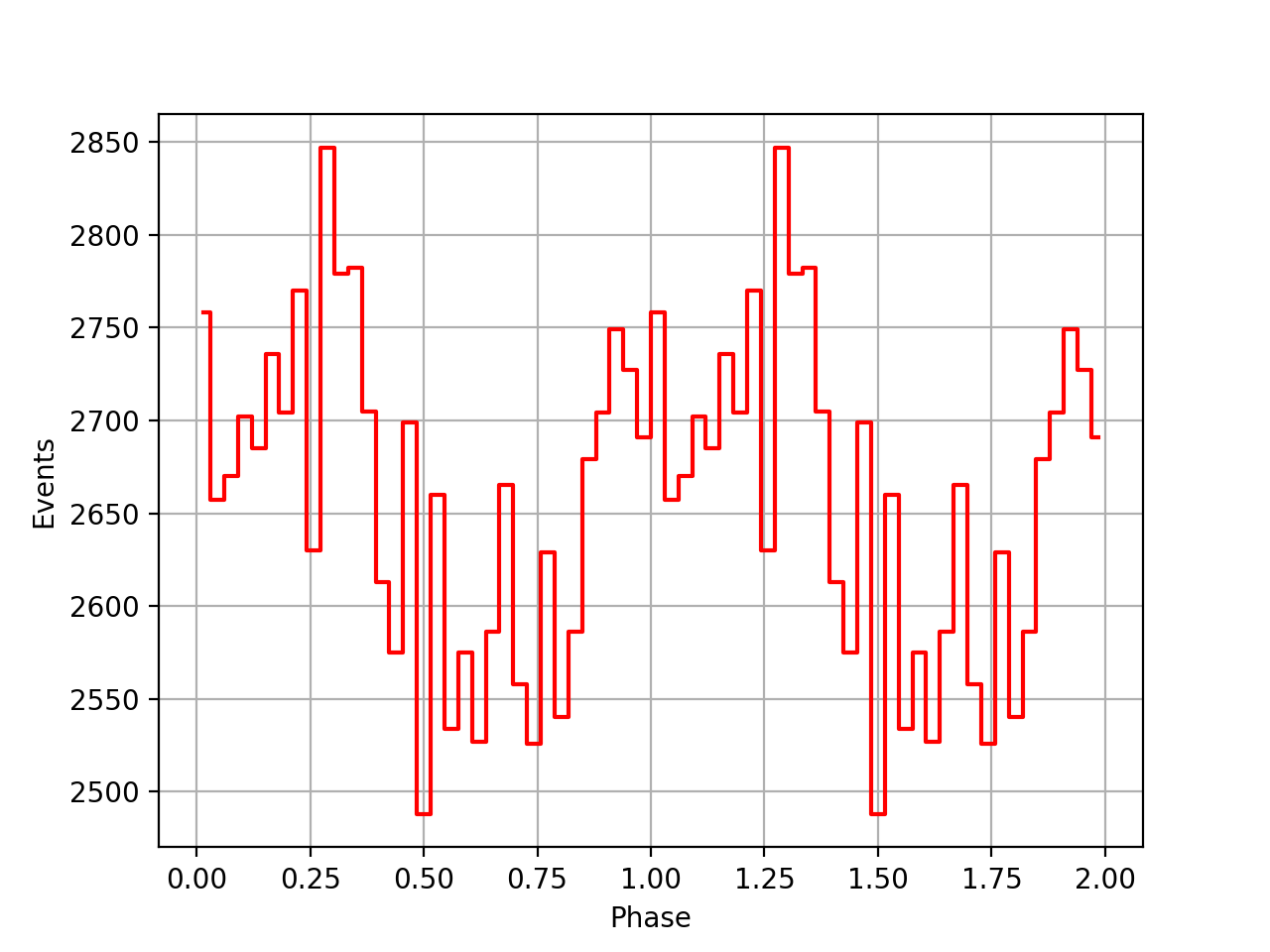
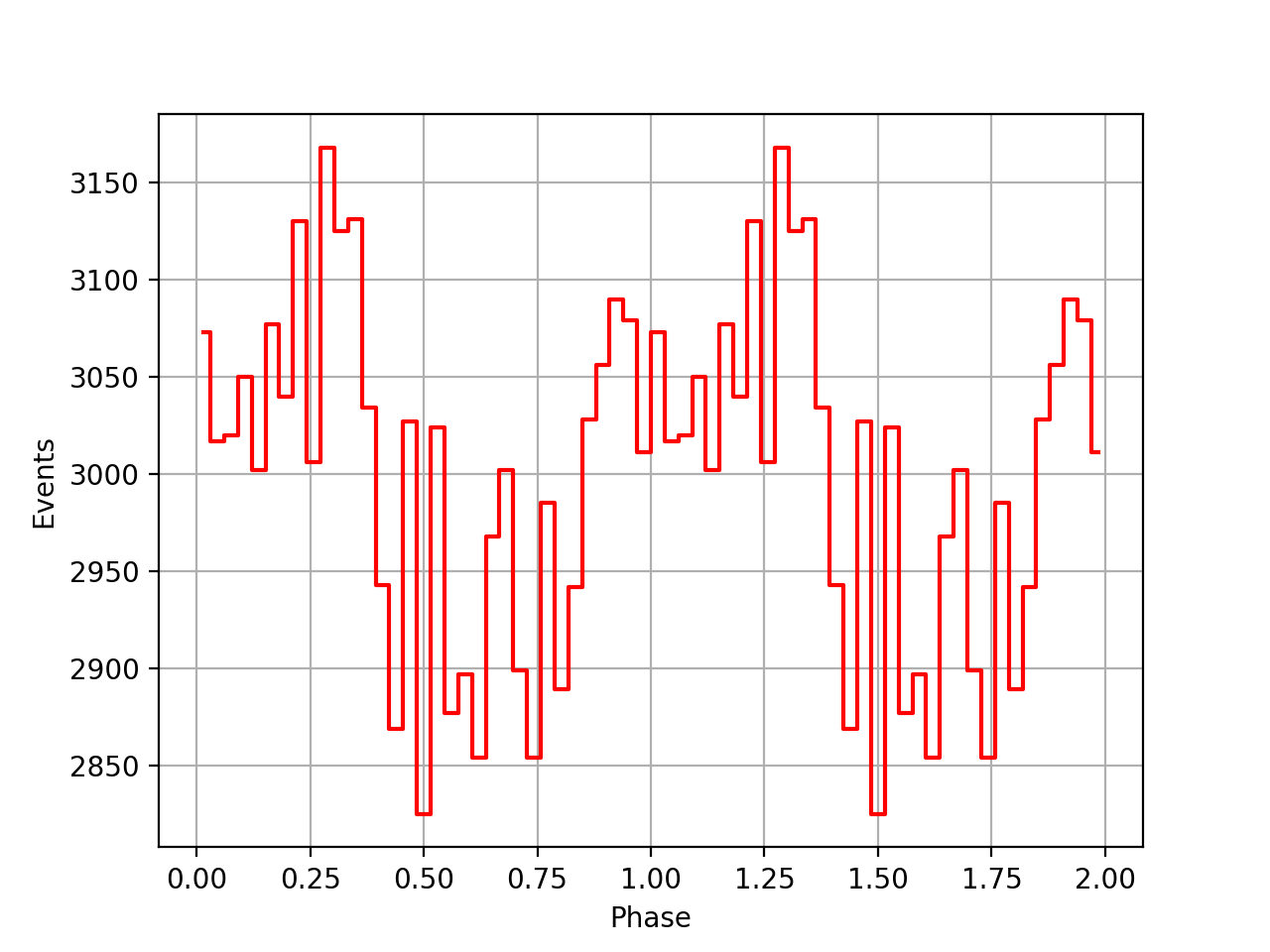
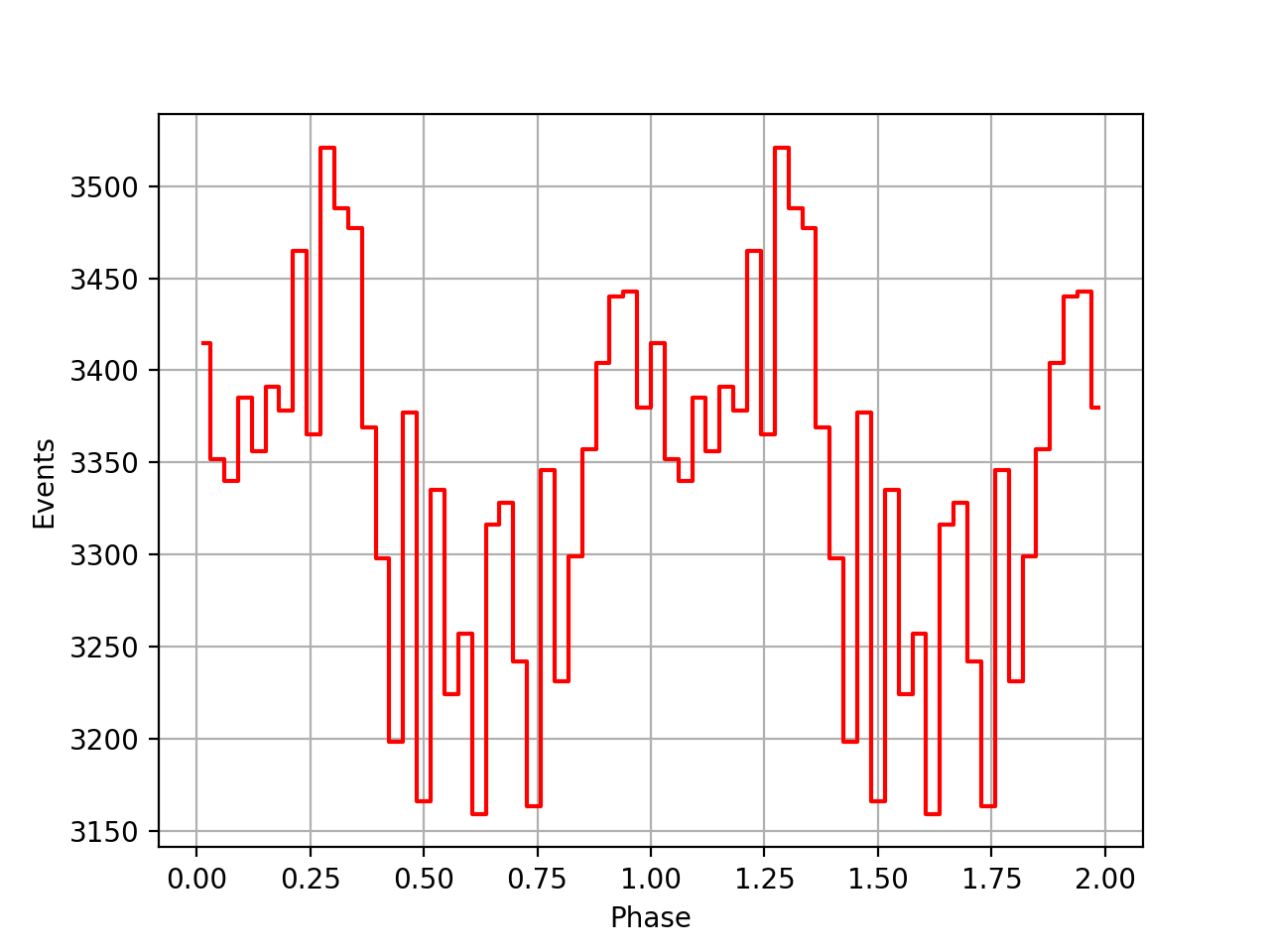
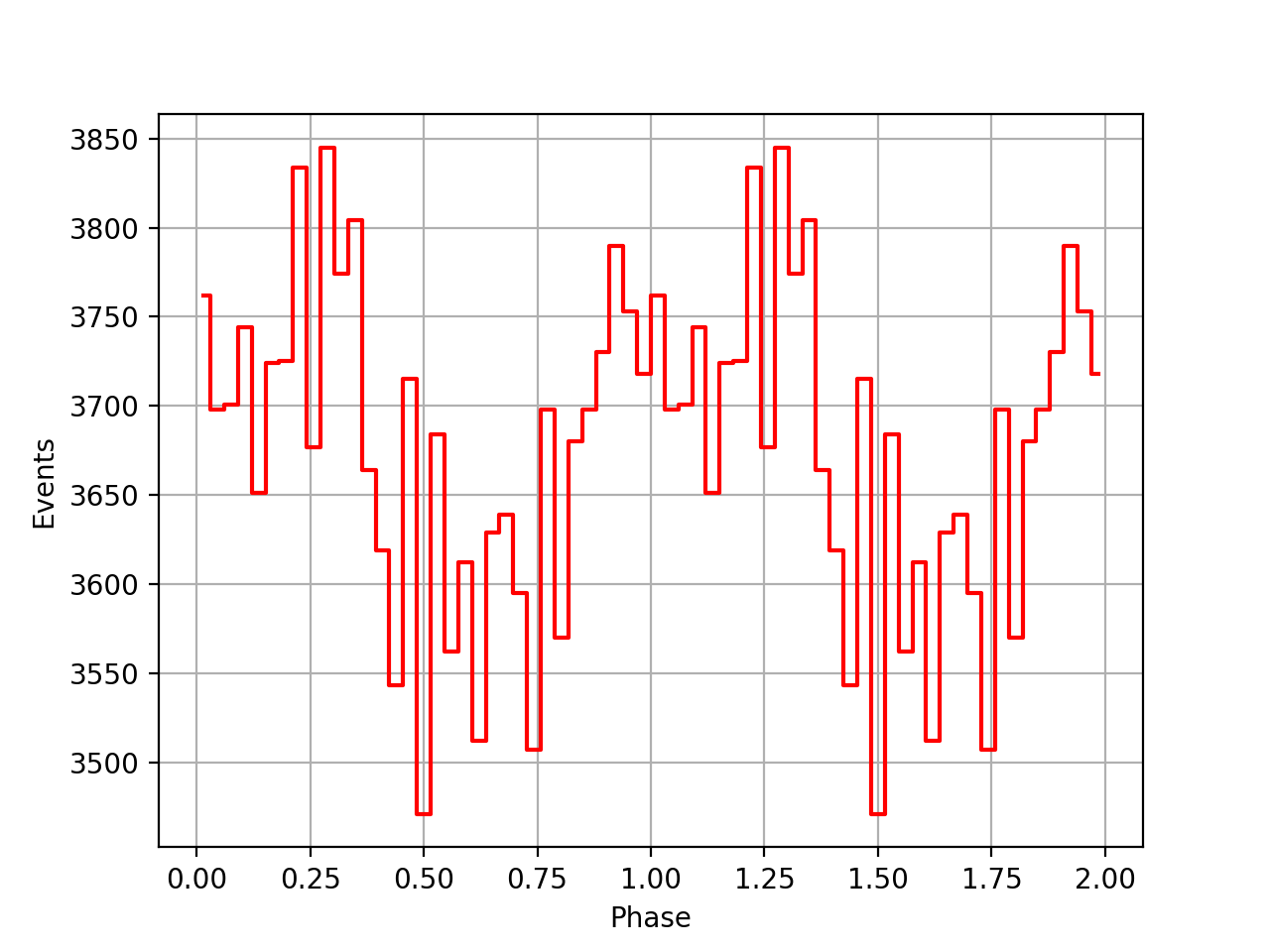
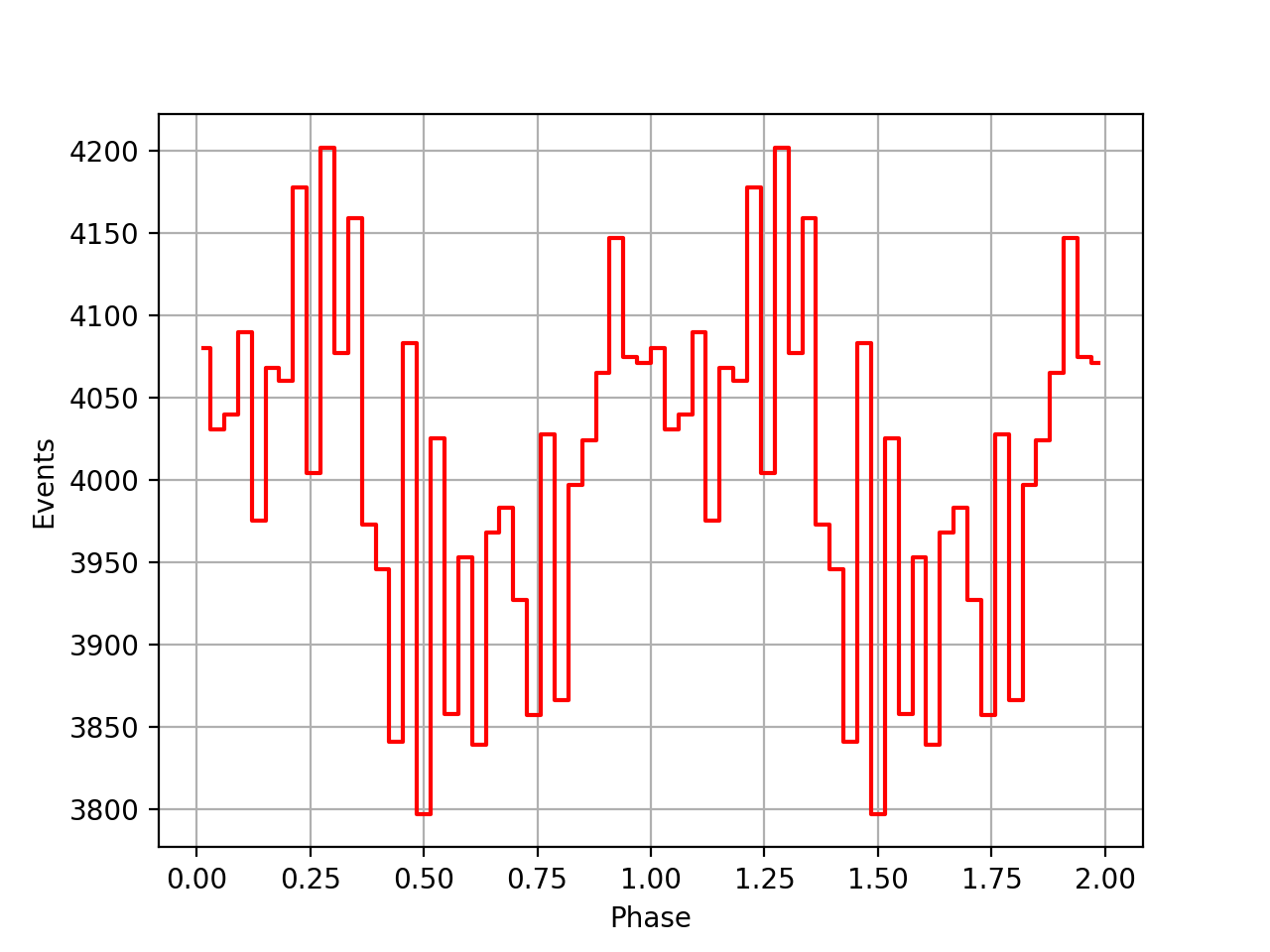
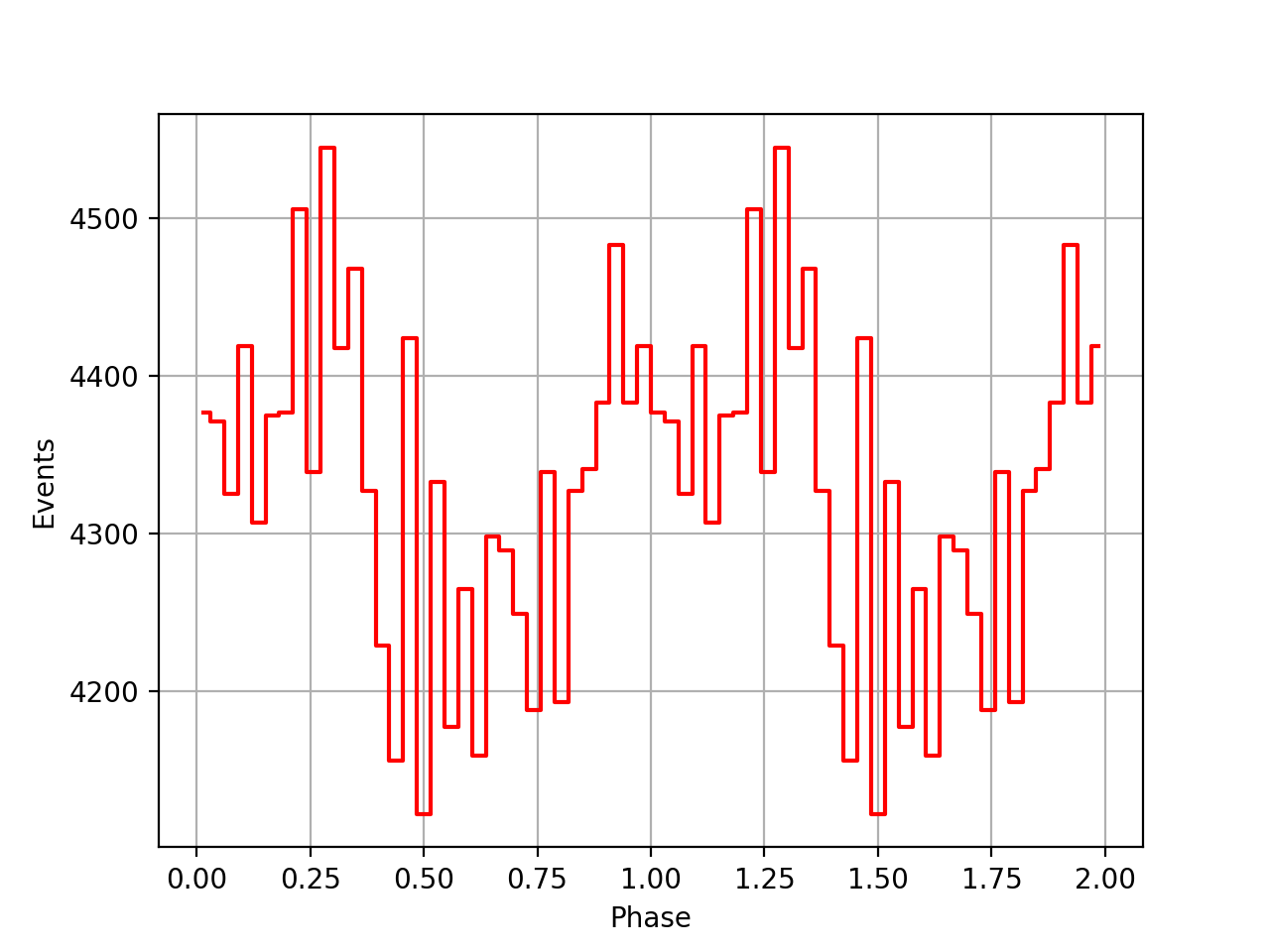
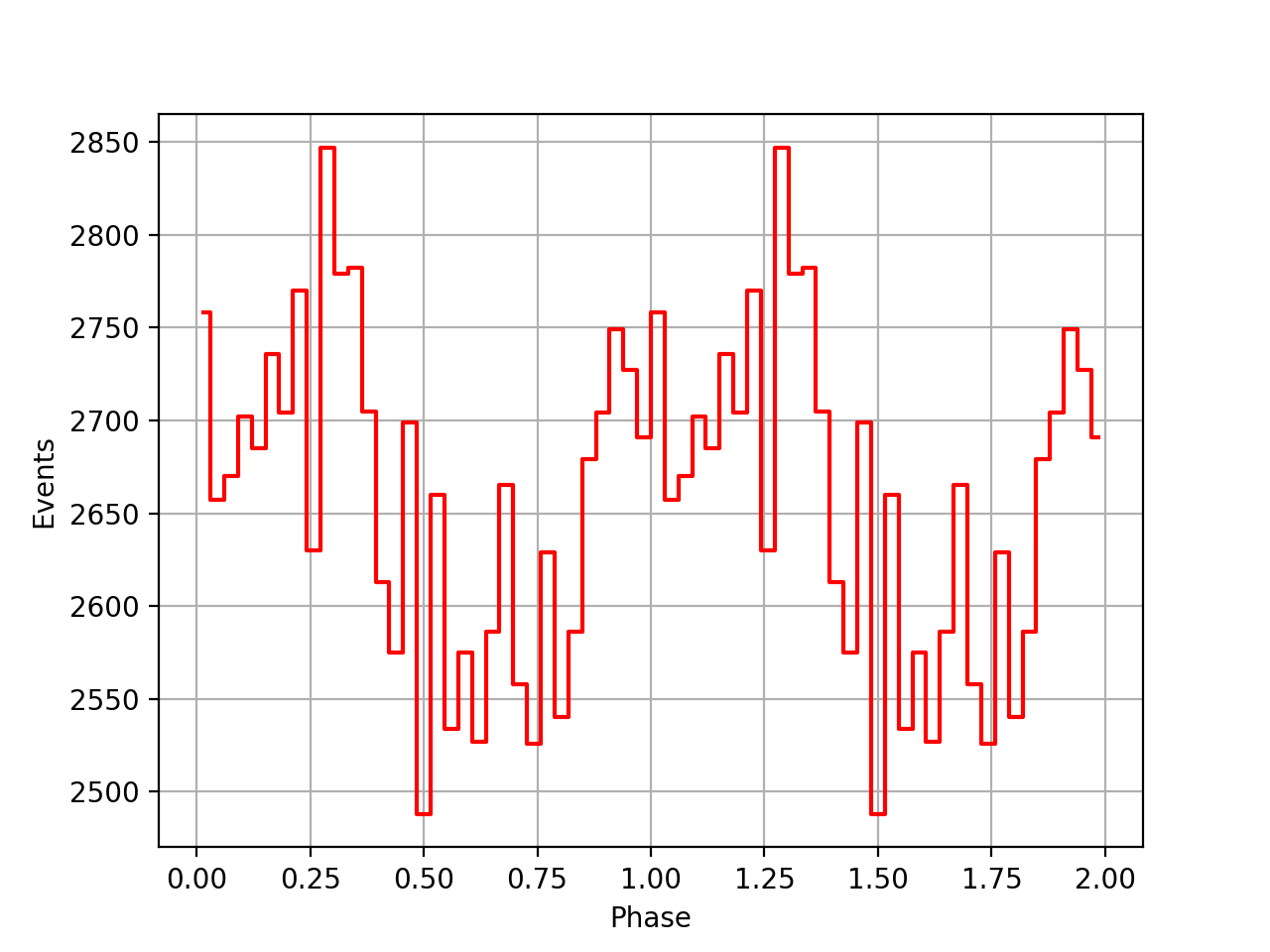
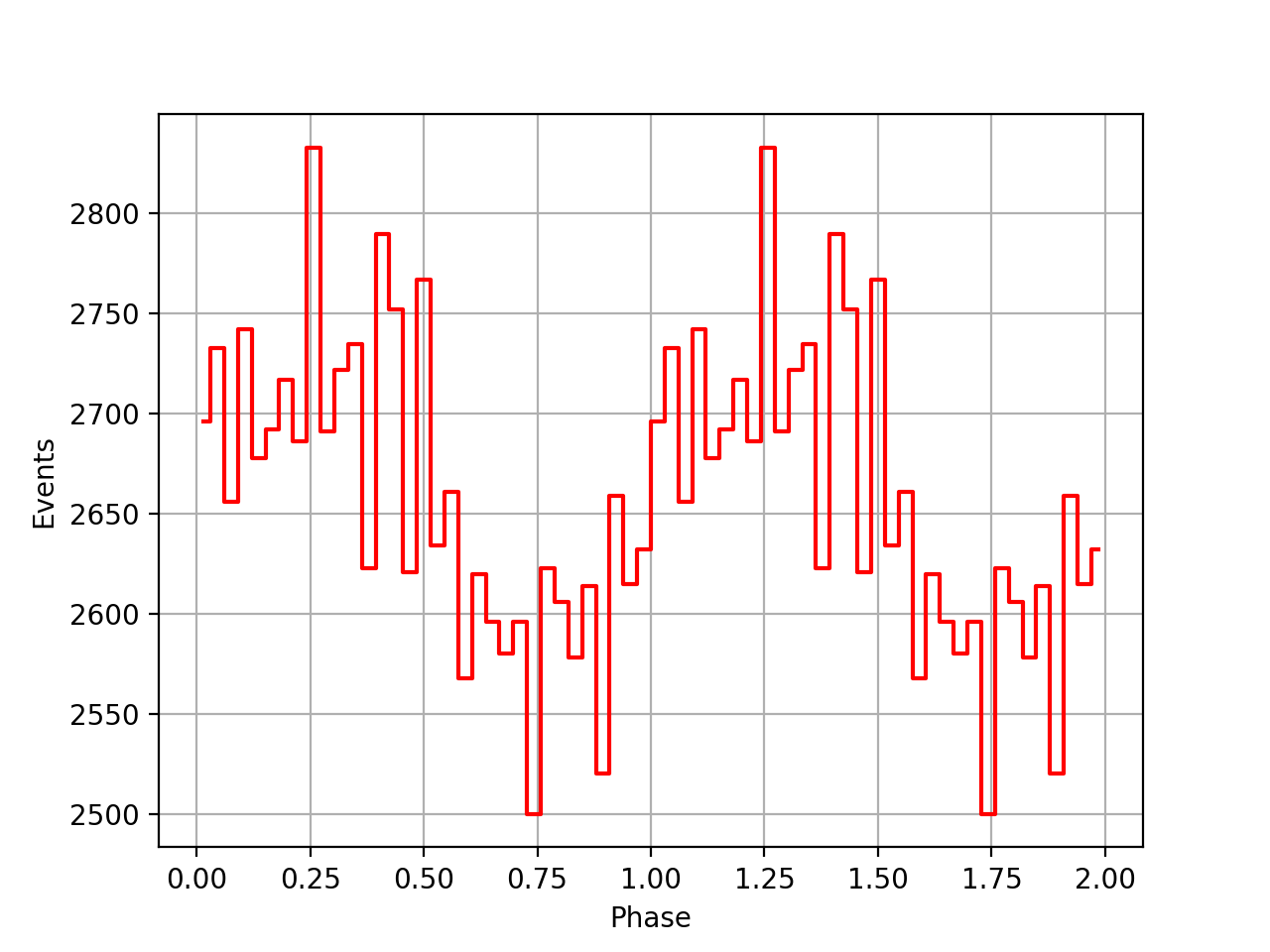
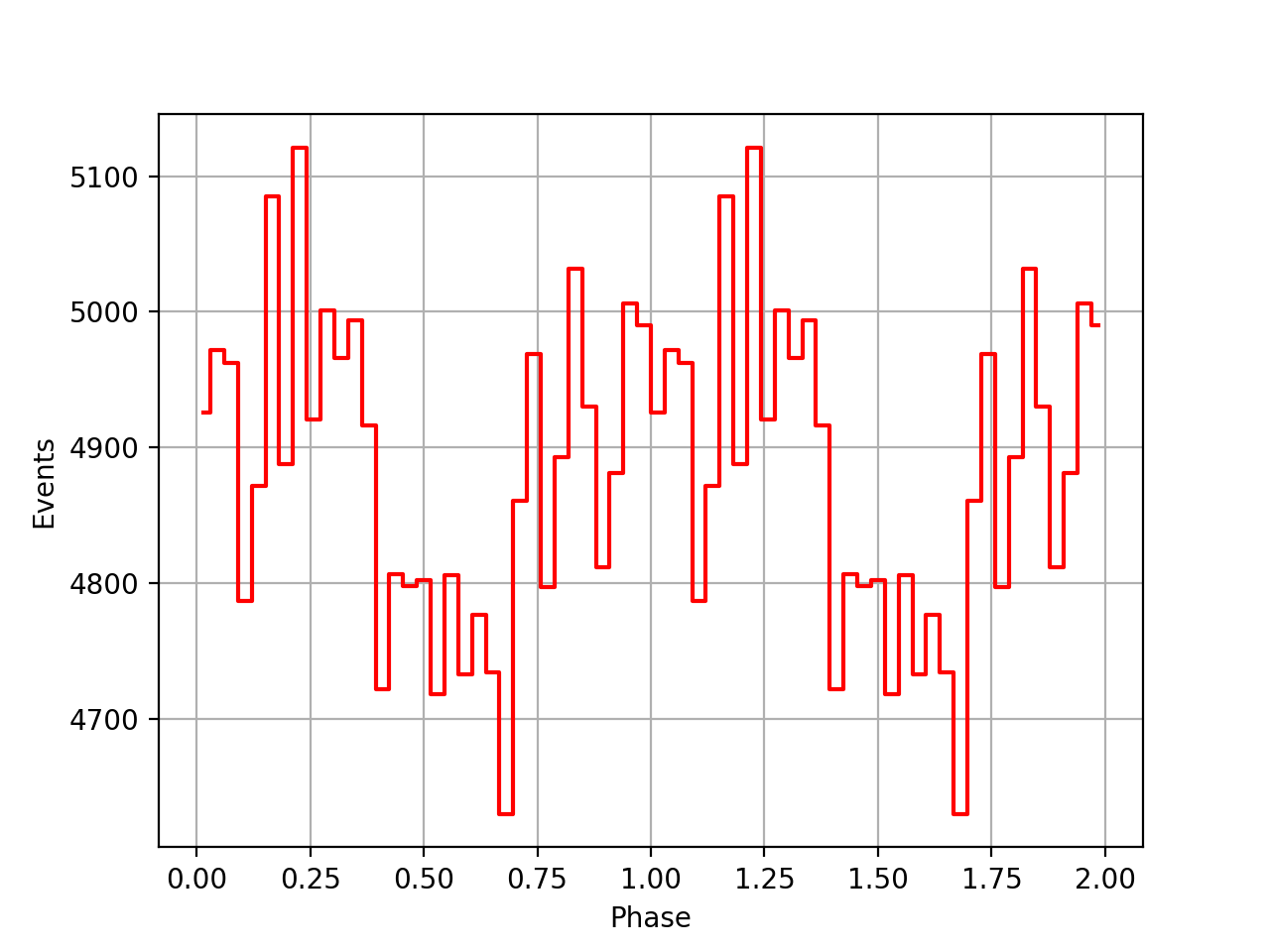
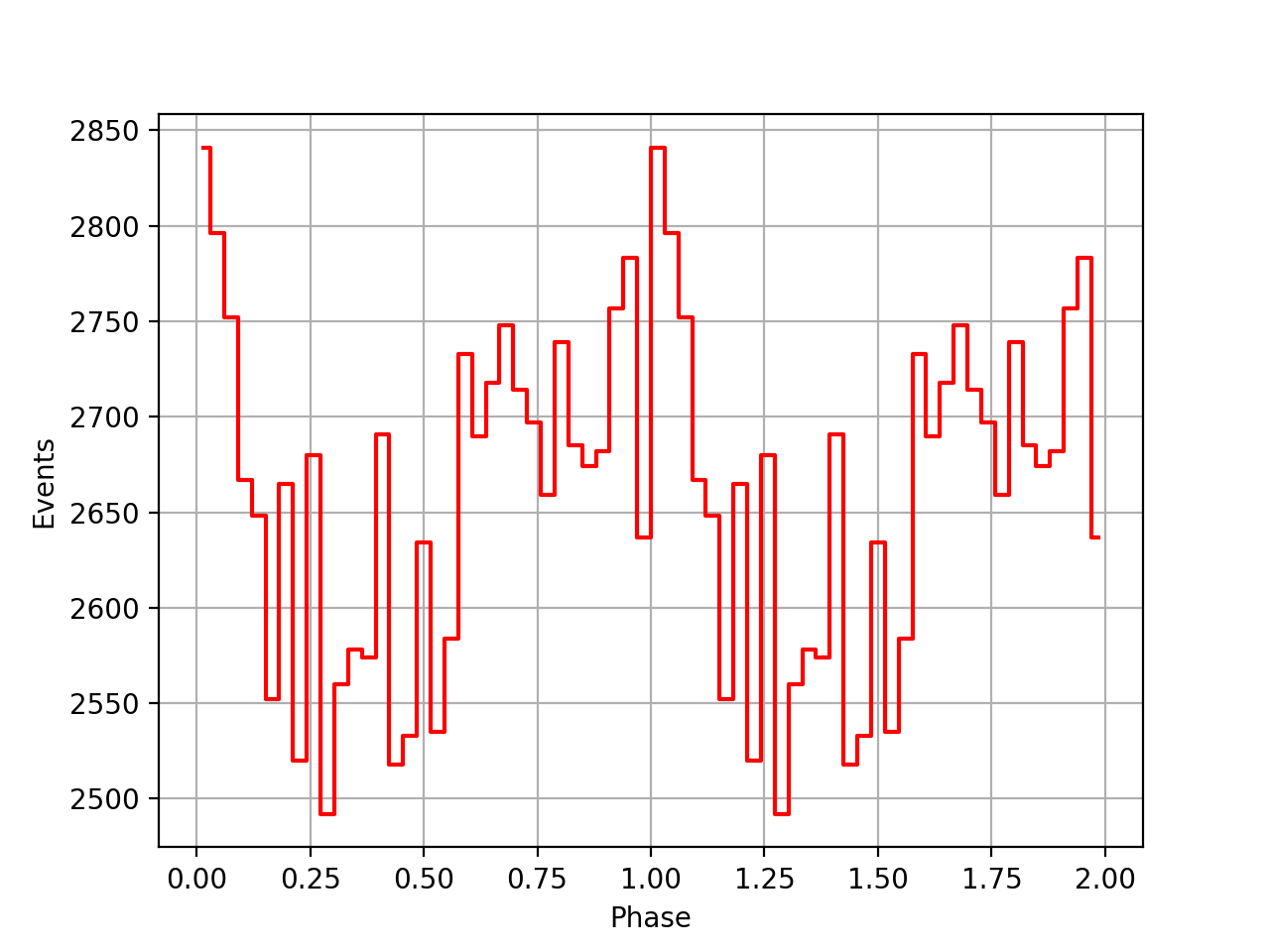
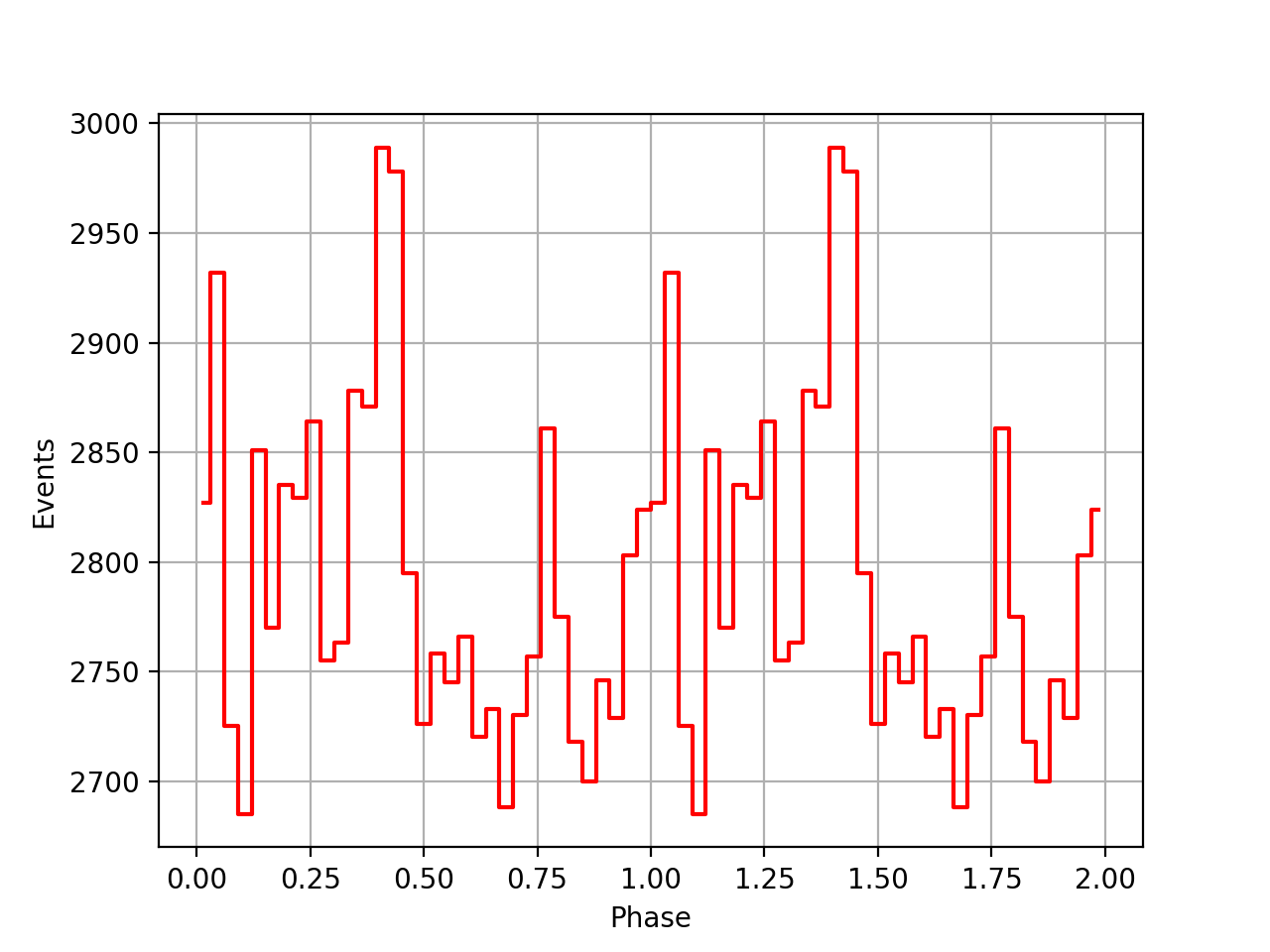
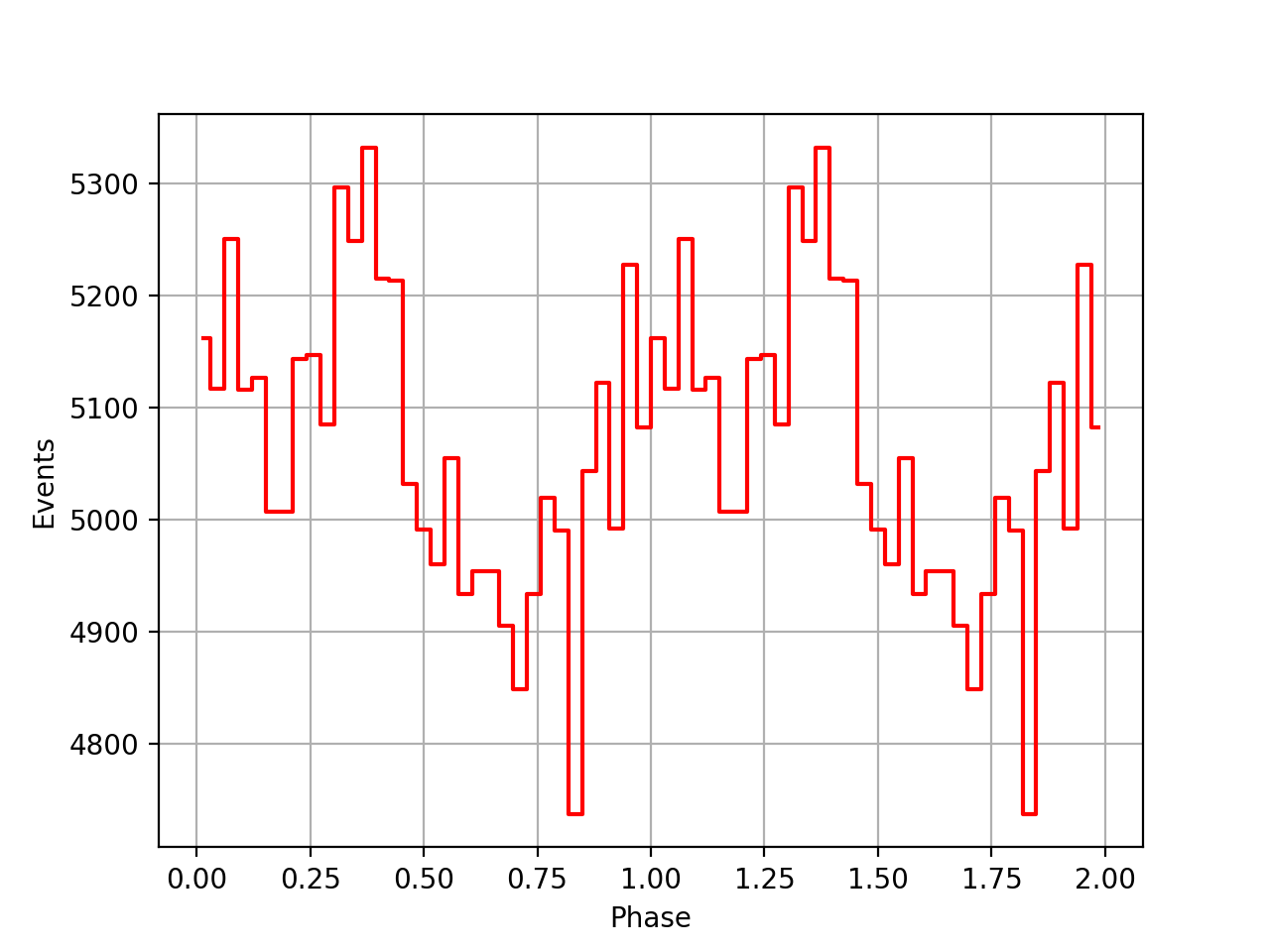
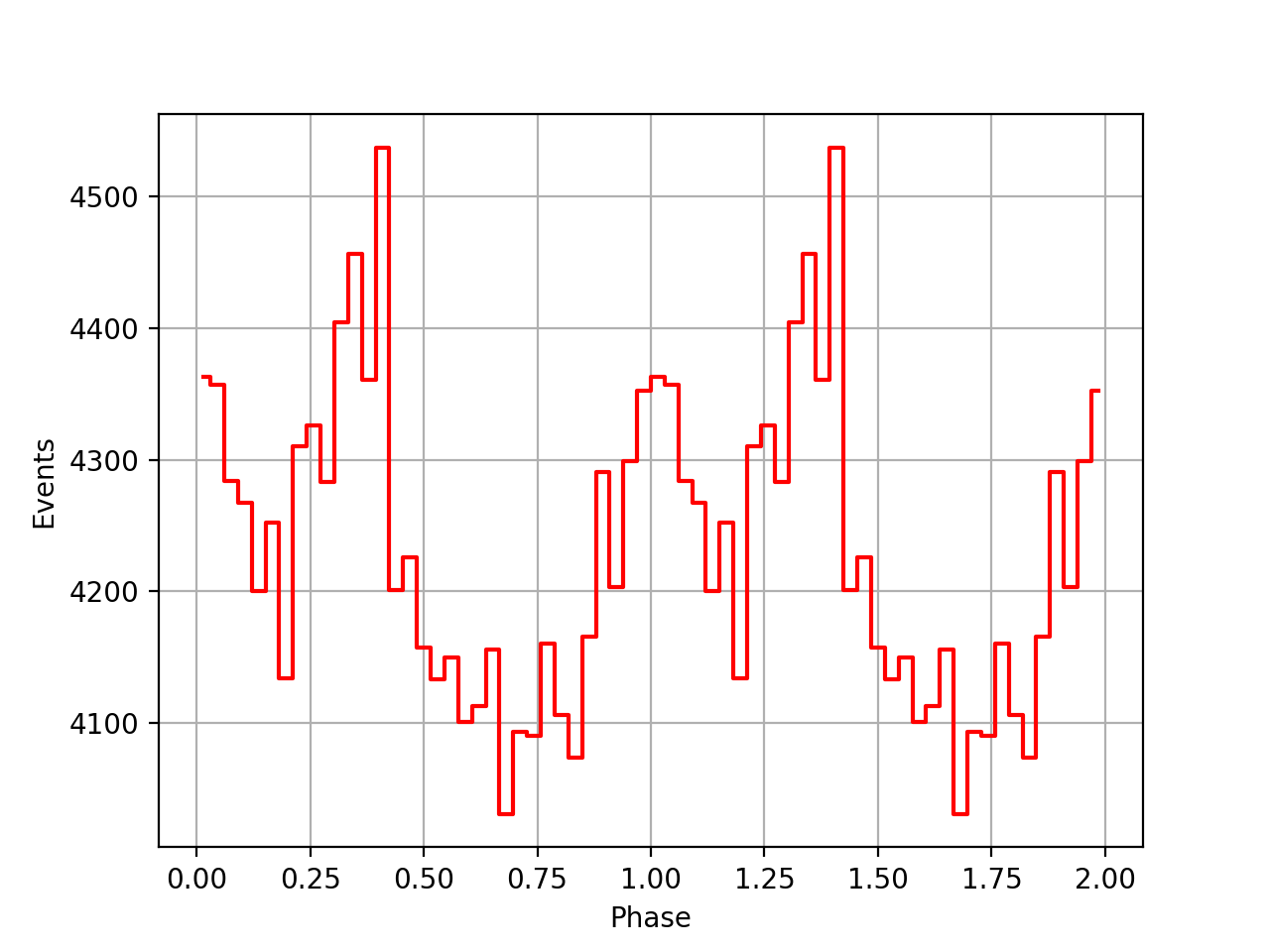
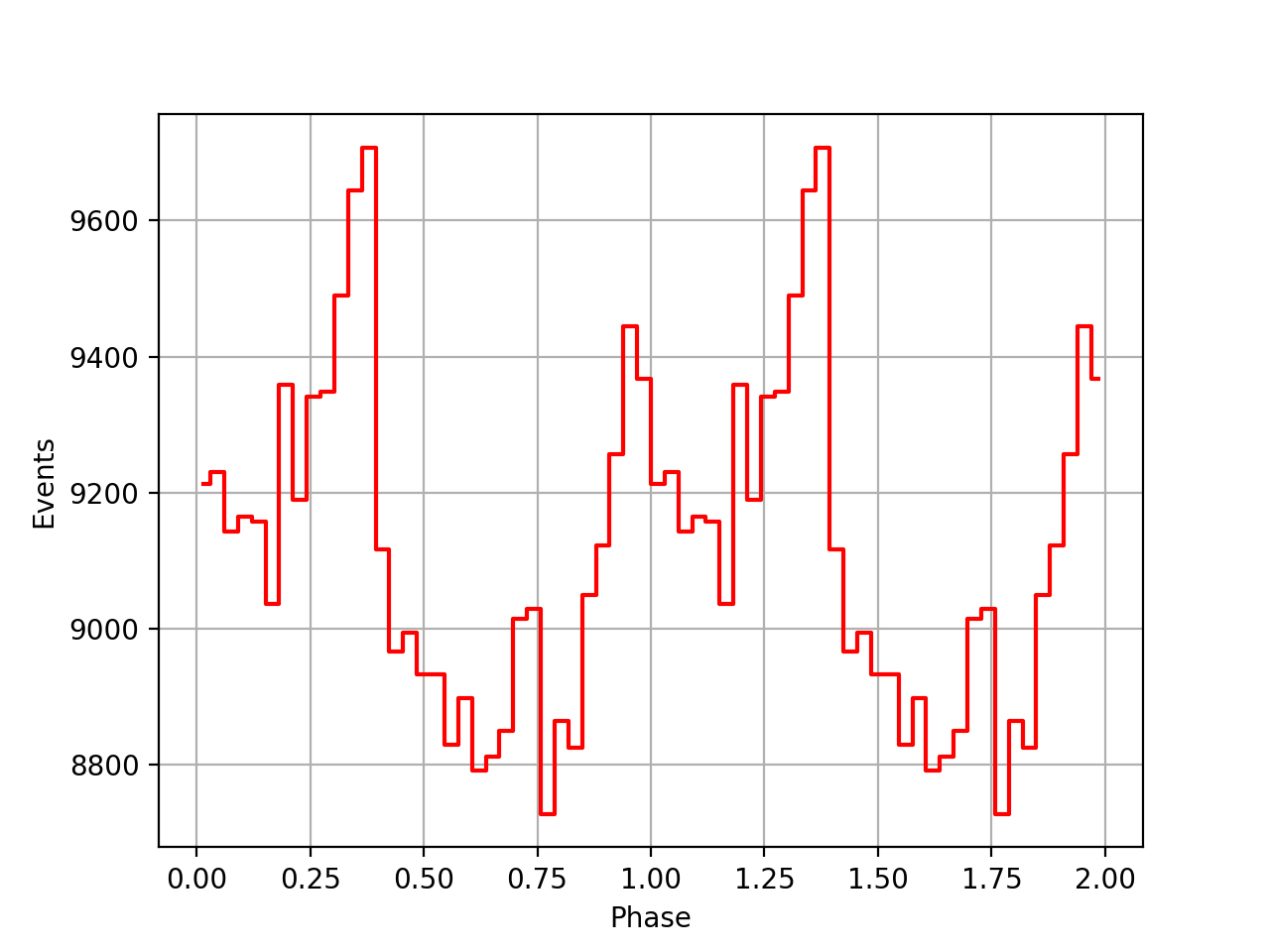
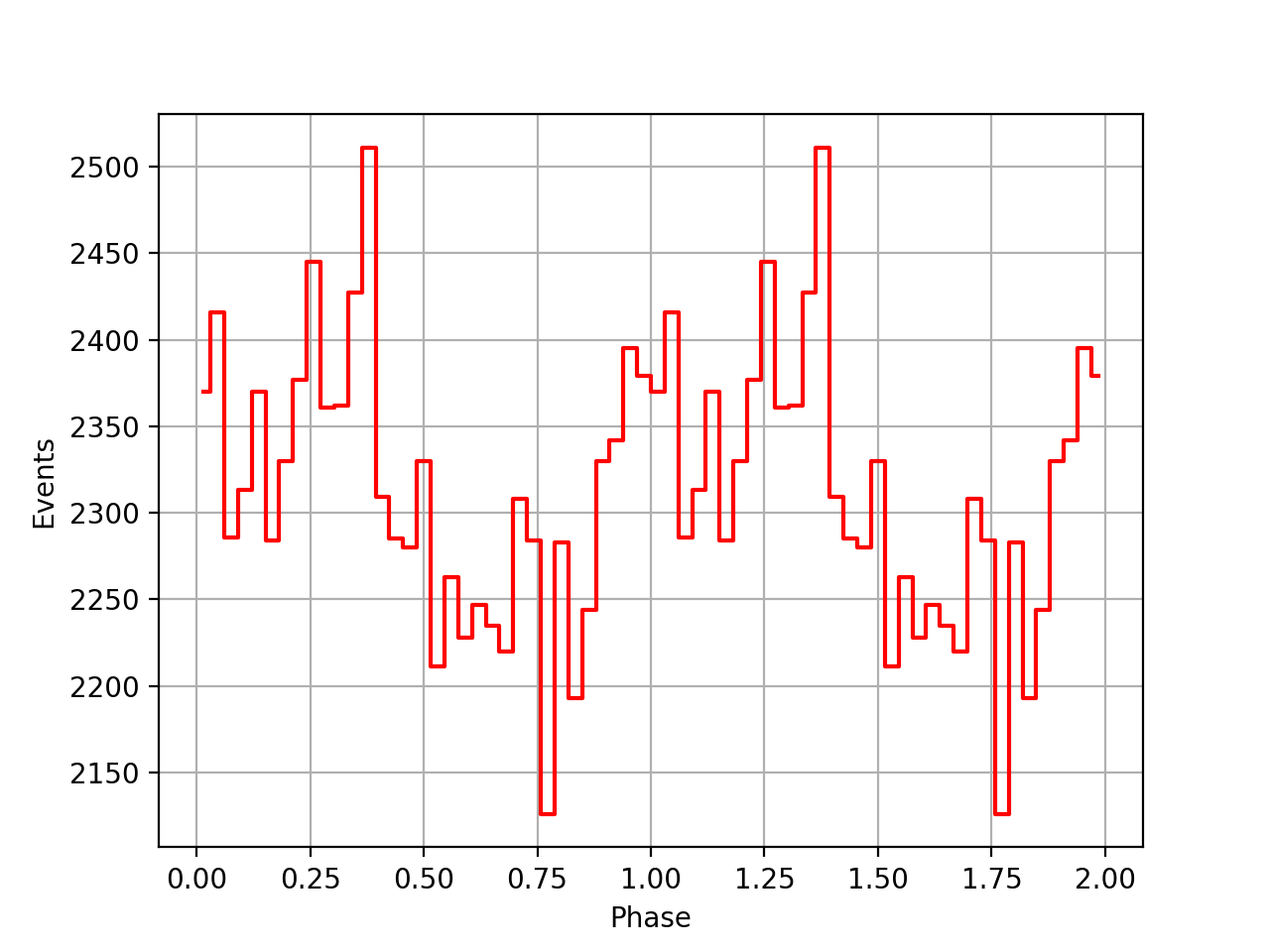
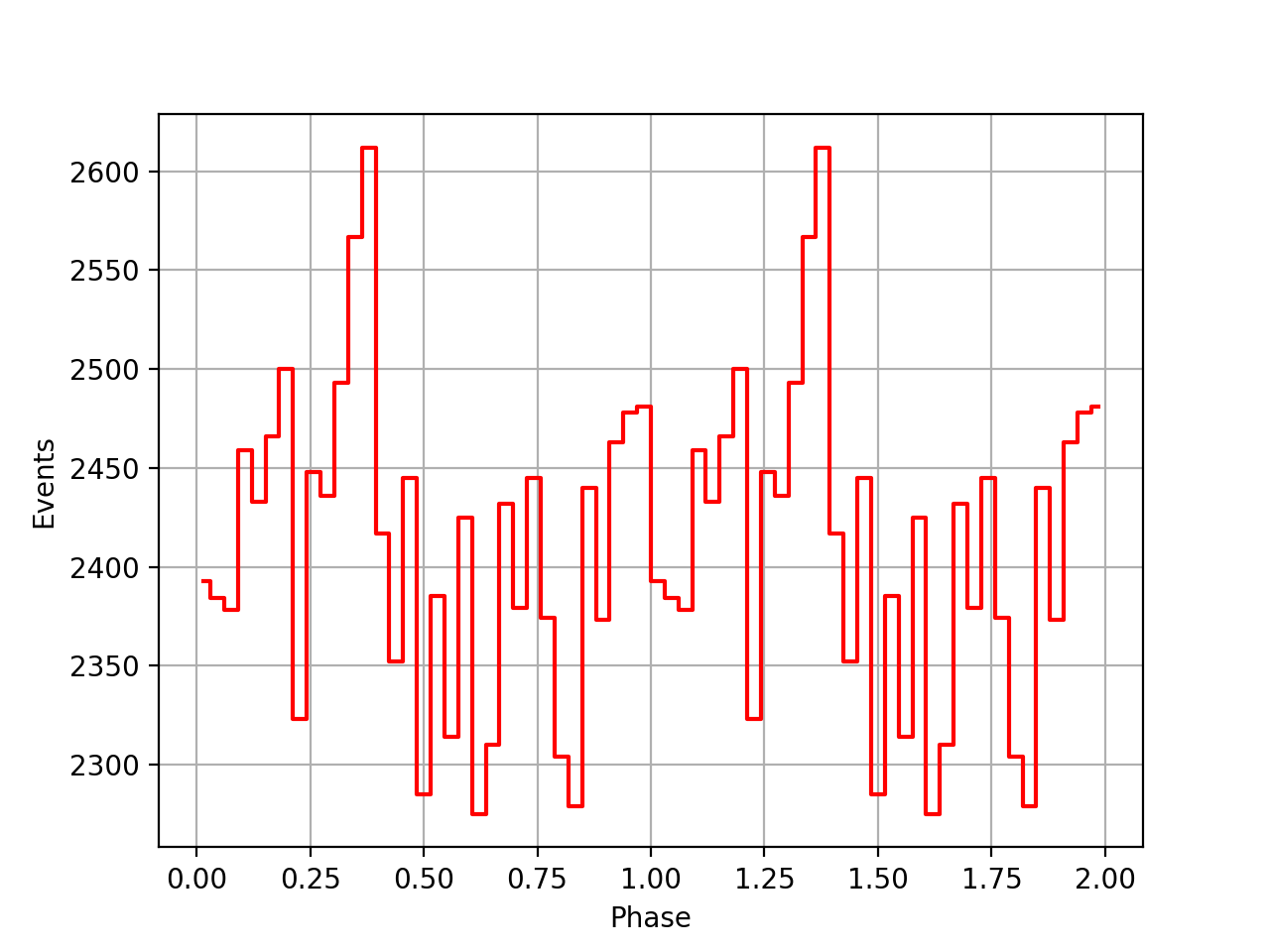
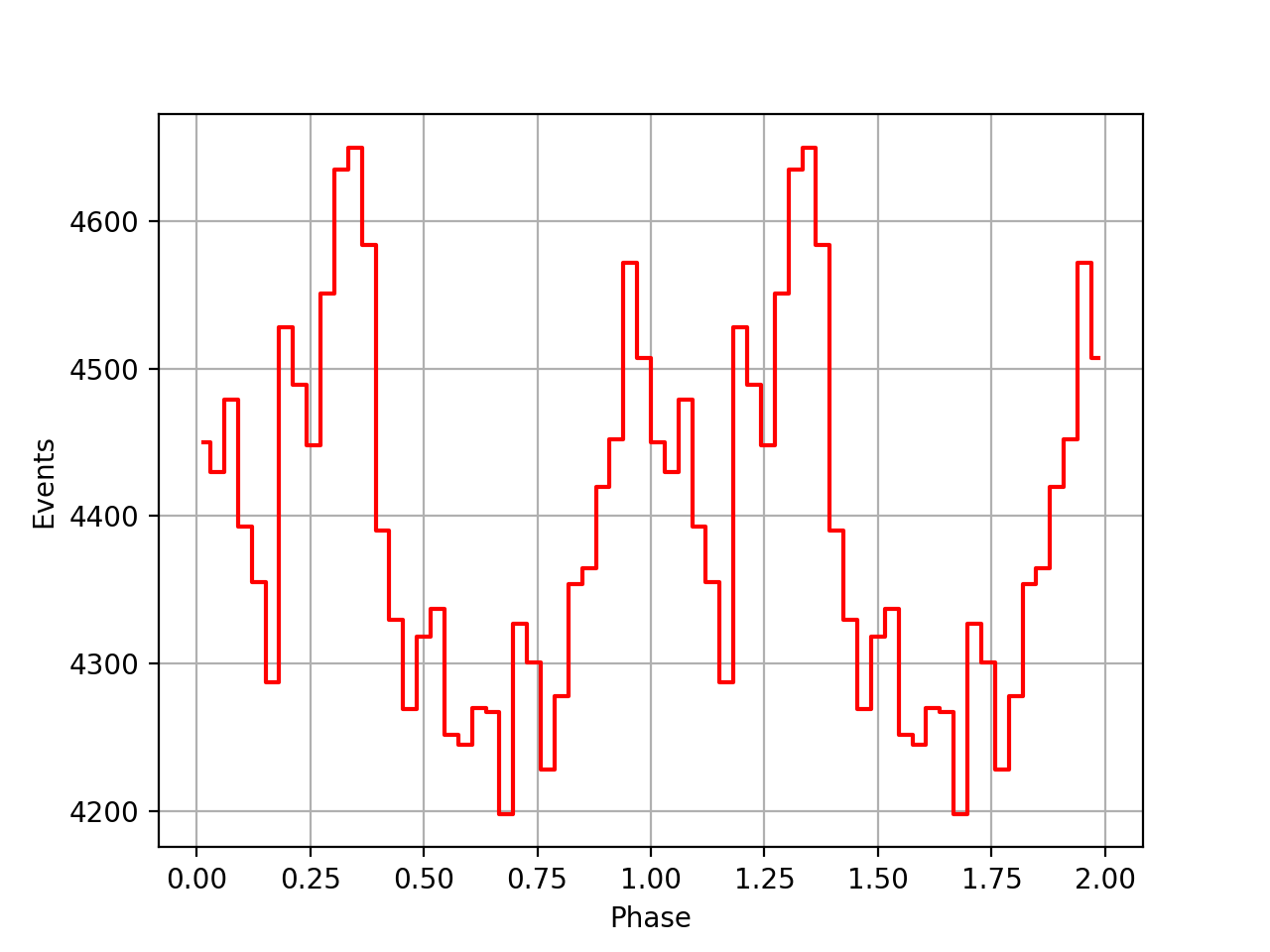
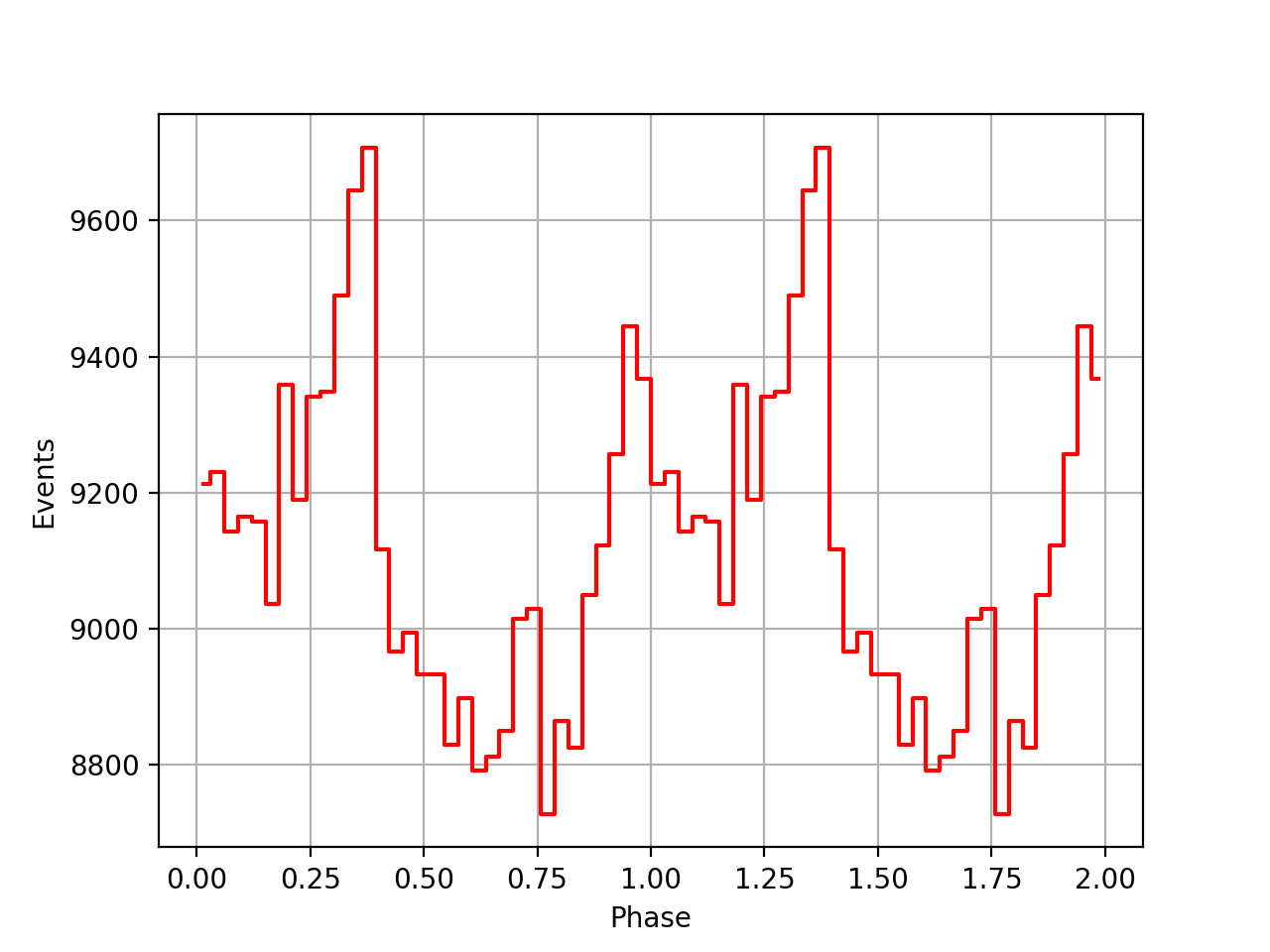
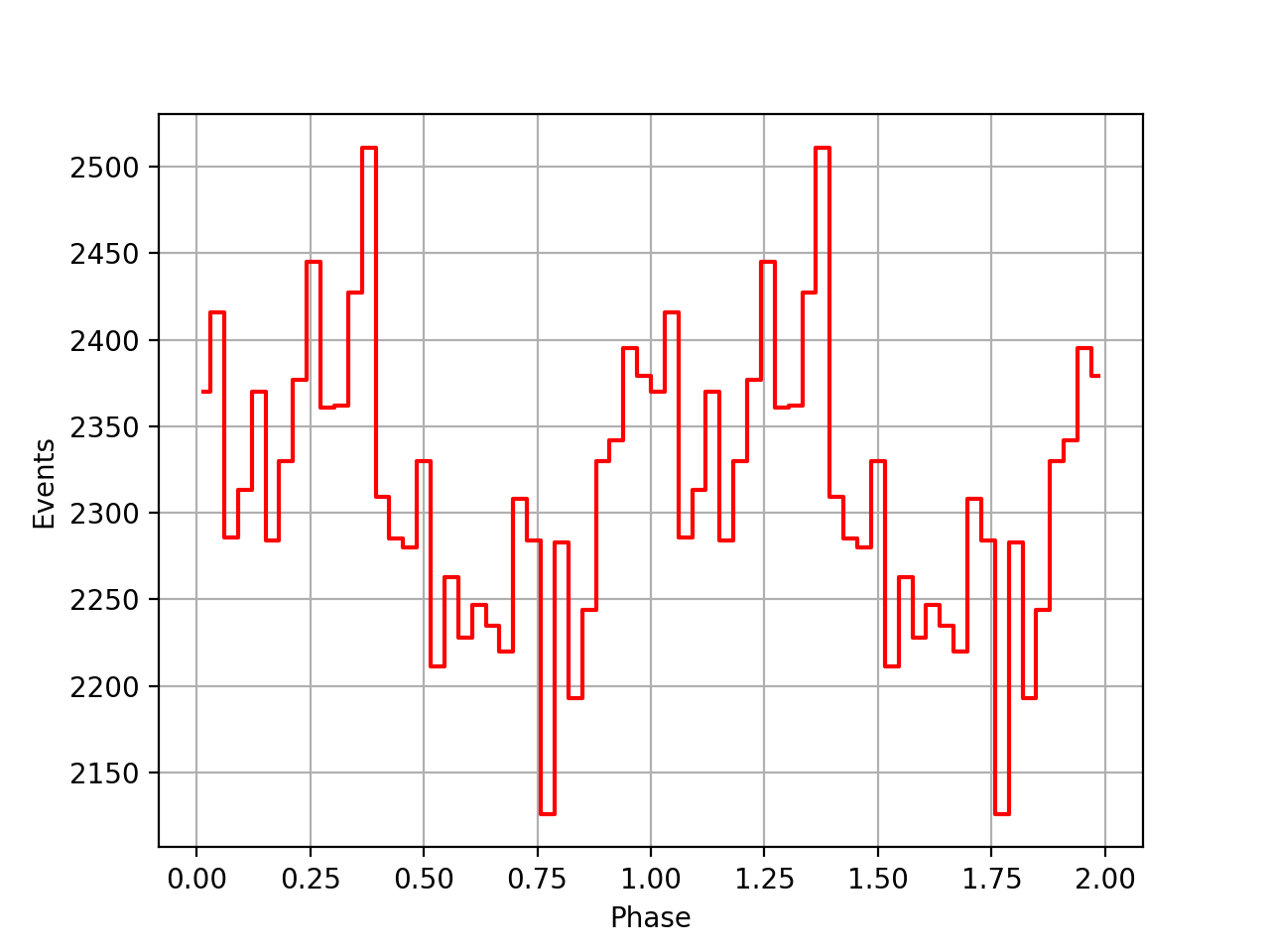
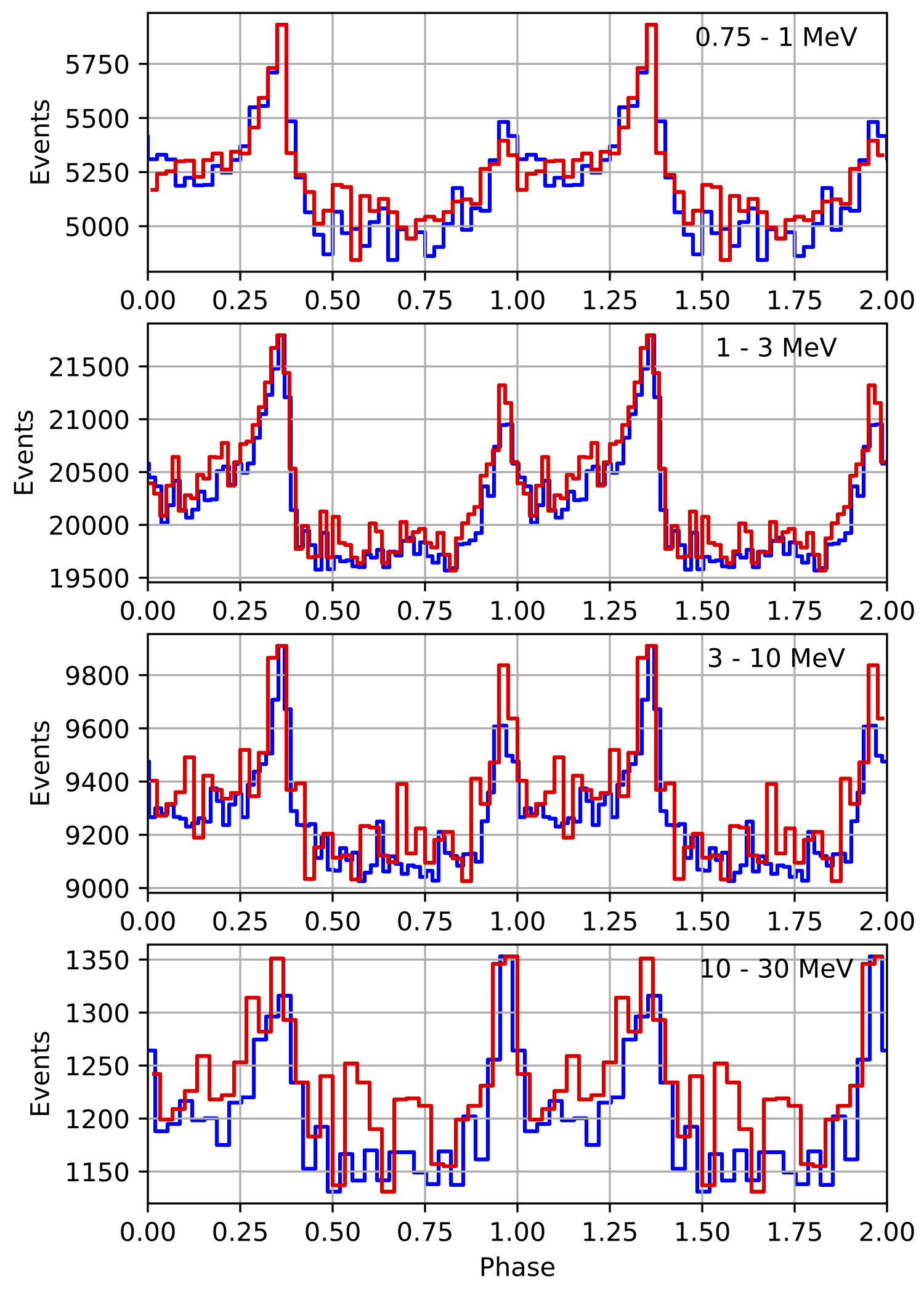
I implemented unit tests and integrated all code. Before closing the issue, hence a nice comparison plot of pulse profiles derived using GammaLib from the HEASARC database with pulse profiles derived by Kuiper et al. (2001) using COMPASS. A phase shift of -0.03 was applied to the profiles by Kuiper et al. (2001).
#48
 Updated by Knödlseder Jürgen about 3 years ago
Updated by Knödlseder Jürgen about 3 years ago
Note that the phase shift cannot be explained by numerical differences. If identical pulsar positions are used, the pulphi.py software produces identical radio phase shifts. Here the result for the Jodrell bank ephemerides
Integer part Tgeo (MJD) ...: 48299 Fraction part Tgeo (MJD) ..: 1.340013e-07 Correction to Tgeo (ms) ...: 0.000000 Correction to Tgeo (days) .: 0.000000 Calculated JD (int) .......: 2448300 Calculated JD (frac) ......: -0.500000 Number of Leap seconds ....: 16 Frequency .................: 29.951601 Frequency derivative ......: -3.777260e-10 Second freq. derivative ...: 0.000000e+00 Pos1 ......................: 0.102808 Pos2 ......................: 0.921371 Pos3 ......................: 0.374841 Pulsar position RA 2000 ...: 83.633217 Pulsar position DEC2000 ...: 22.014464 UTC--> TDT ................: 58.184000 sec TDT--> TDB ................: 0.001047 sec UTC--> TDB ................: 58.185047 sec Traveltime difference .....: 255.737957 sec Relativistic delay ........: -0.000004 sec Total delay ...............: 313.923009 sec Time diff. to nom. epoch ..: 313.934586 sec Radio-phase 0 at nom.epoch : 0.843473 === GPulsarEphemeris === Pulsar name ...............: PSR B0531+21 Pulsar Right Ascension ....: 83.633225 deg Pulsar Declination ........: 22.0144583333333 deg Time system of ephemeris ..: UTC Reference epoch ...........: MJD 48299 Phase .....................: -0.845097897454252 Frequency .................: 29.9516010684378 Hz Frequency derivative ......: -3.77726e-10 Hz/s 2nd frequency derivative ..: 0 Hz/s^2 Period ....................: 33.3871968218011 ms Validity MJD range ........: 48281.9993265741 - 48315.9993265741 Validity UTC range ........: 1991-01-25T23:59:02 - 1991-02-28T23:59:02 pulphi radio phase ........: -0.210862 GammaLib radio phase ......: -0.210863 Difference ................: 0.000001and here the results for the Princeton ephemerides
Integer part Tgeo (MJD) ...: 48299 Fraction part Tgeo (MJD) ..: 1.340013e-07 Correction to Tgeo (ms) ...: 0.000000 Correction to Tgeo (days) .: 0.000000 Calculated JD (int) .......: 2448300 Calculated JD (frac) ......: -0.500000 Number of Leap seconds ....: 16 Frequency .................: 29.951601 Frequency derivative ......: -3.777260e-10 Second freq. derivative ...: 0.000000e+00 Pos1 ......................: 0.102807 Pos2 ......................: 0.921371 Pos3 ......................: 0.374841 Pulsar position RA 2000 ...: 83.633225 Pulsar position DEC2000 ...: 22.014458 UTC--> TDT ................: 58.184000 sec TDT--> TDB ................: 0.001047 sec UTC--> TDB ................: 58.185047 sec Traveltime difference .....: 255.738011 sec Relativistic delay ........: -0.000004 sec Total delay ...............: 313.923063 sec Time diff. to nom. epoch ..: 313.934641 sec Radio-phase 0 at nom.epoch : 0.845098 === GPulsarEphemeris === Pulsar name ...............: PSR B0531+21 Pulsar Right Ascension ....: 83.633225 deg Pulsar Declination ........: 22.0144583333333 deg Time system of ephemeris ..: UTC Reference epoch ...........: MJD 48299 Phase .....................: -0.845097897454252 Frequency .................: 29.9516010684378 Hz Frequency derivative ......: -3.77726e-10 Hz/s 2nd frequency derivative ..: 0 Hz/s^2 Period ....................: 33.3871968218011 ms Validity MJD range ........: 48281.9993265741 - 48315.9993265741 Validity UTC range ........: 1991-01-25T23:59:02 - 1991-02-28T23:59:02 pulphi radio phase ........: -0.845098 GammaLib radio phase ......: -0.845098 Difference ................: -0.000000
The pulse shift can however be explained by differences in the assumed position of the Crab pulsar. This is illustrated in the table below where small shifts (in units of degrees) were added to the pulsar position in the pulphi.py computation, while no shifts were applied in the GammaLib computation. A position inaccuracy of 0.54 arcsec in Right Ascension leads to a phase shift of -0.03! In comparison, the difference in Right Ascension between the SIMBAD ICRS position and the position provided in the Princeton file is 0.5355.
| RA shift | DEC shift | Phase difference |
| 0.0 | 0.0024 | -0.030491 |
| 0.00015 | 0.0 | -0.030533 |
| 0.0001 | 0.0008 | -0.030520 |
Note that according to http://simbad.u-strasbg.fr/simbad/sim-ref?bibcode=2011A%26A...533A..10L the Crab pulsar proper motion in Right Ascension is -13.0±0.2mas/yr and in Declination is +2.9±0.1mas/yr. Since the SIMBAD position is for the epoch 2000 while the ephemerides are for 1991, this translated into a motion of 0.117 arcsec in Right Ascension and 0.0119 arcsec in Declination. Hence the proper motion alone cannot explain the differences in the pulsar position.